JKBOSE 9th Class Mathematics Solutions Chapter 11 Construction
JKBOSE 9th Class Mathematics Solutions Chapter 11 Construction
JKBOSE 9th Class Mathematics Solutions Chapter 11 Construction
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Construction Textbook Questions and Answers
INTRODUCTION
Figures, which are necessary to prove a theorem or solving exercies are only rough and are drawn only to give proper reasoning. Sometimes we need an accurate figure for using them in some specified trade, for example – to draw a map of building to be constructed, to design tools, and various parts of a machine, to draw road maps etc. To draw such figures we need some basic geometrical instruments. We must have a geometry box which contains the following :
(i) A graduated scale, on whose one edge marked centimeters and millimeters and on the other side inches and their parts.
(ii) A pair of set-squares, one with angles 60° and 30° and other with angles 45° and 45°.
(iii) A pair of compasses (or a compass) with provision of fitting a pencil at one end.
(iv) A pair of dividers (or divider) with adjustments.
(v) A protractor.
Usually, all these instruments are needed in drawing a geometrical figure, such as a triangle, a circle, a quadrilateral, a polygon etc. with given measurements. But a geometrical construction is the process of drawing a geometrical figure using only two instruments – an ungraduated ruler, also called a straight edge and a compass. In construction where measurements are also required you may use graduated scale and protractor also. In this chapter, you will learn about some basic constructions and some other constructions.
Basic Constructions
In Class VI, you have learnt how to construct a circle, perpendicular bisector of line segment, angle of 60°, 30°, 120°, 90° and 45°, bisector of a given angle etc., without giving any justification to these. constructions. In this section, you will learn to construct some of these with proper justification to these constructions.
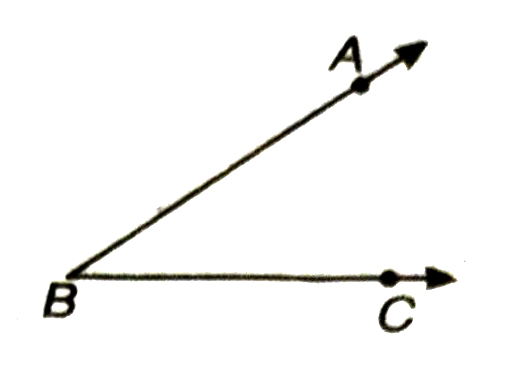
Construction : To construct bisector of a given angle. Given an angle ABC you are to required to construct the bisector of ∠ABC.
Steps of Construction.
Step. 1. Draw an angle ABC.
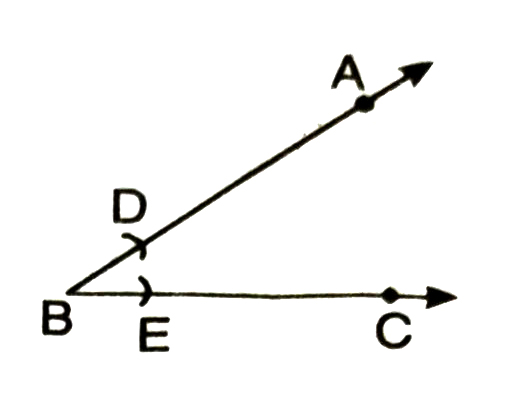
Step 2. With B as centre and with a suitable radius, draw an arc to cut BA and BC at D and E respectively.
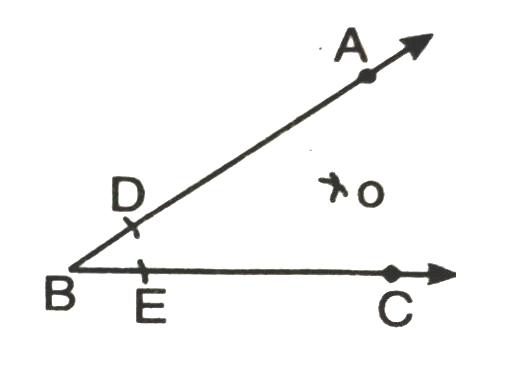
Step 3. With D and E as centre and radius more than half of DE, draw two arcs cutting at O.
Step 4. Join BO and produce it to form ray BF. Measure ∠ABF and ∠FBC. Thus, BO is the bisector of ∠ABC.
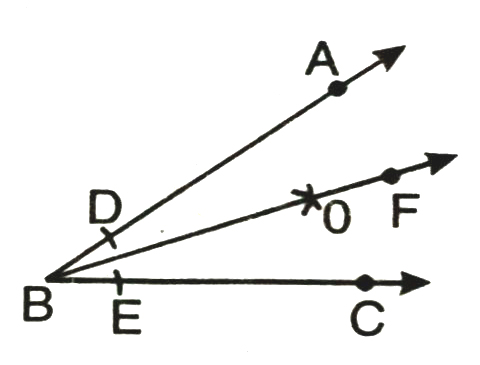
Verification. We measure ∠ABF and ∠FBC with a protractor and verified that ∠ABF = ∠FBC.
REMARK. Since BF bisects LABC. Therefore, it follows that ∠ABF = ∠FBC = ∠ABC.
Justification of Construction :
Join DO and EO.
In ΔBOD and ΔBOE,
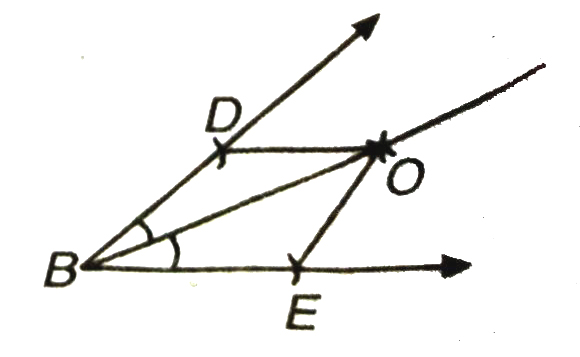
BD = BE (Radii of same arcs)
DO = EO (Arcs of equal radii)
BO = BO (Common)
Therefore ΔBOD ≅ ΔBOE (By SSS Rule)
This gives ∠OBD = ∠OBE (CPCT)
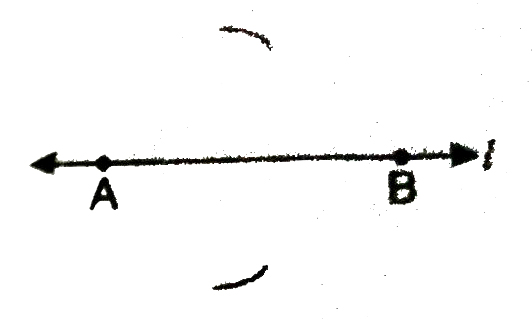
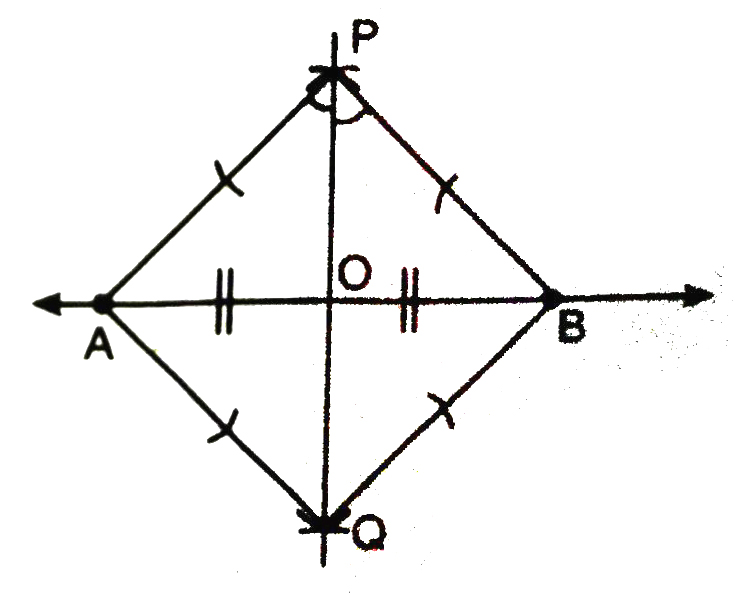
Construction. To construct the perpendicular bisector of a given line segment.
Given a line segment AB, you are required to construct the perpendicular bisector of AB.
Steps of Construction :
1. Draw a line l. Mark a line segment, AB on given line l.

2. With centre A and radius > 1/2 (AB), draw arcs, one on each side of AB.
3. With centre B and the same radius as before, draw arcs, cutting the previously drawn arcs at P and Q respectively.
4. Join P and Q meeting AB at O. Then PQ is the perpendicular bisector of line segment AB.
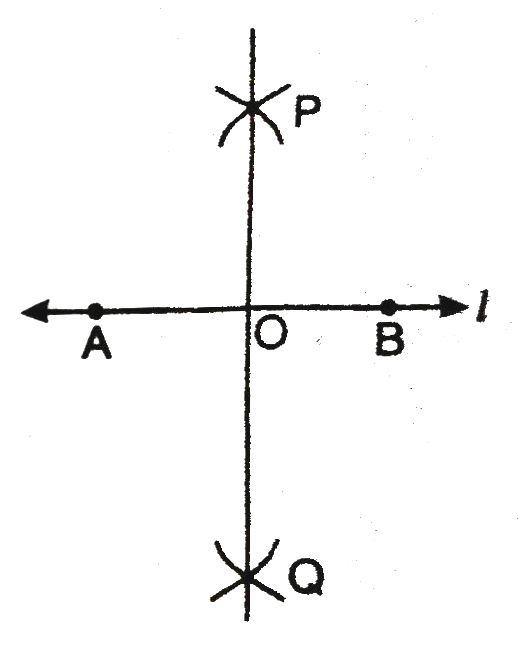
Verification. Measure ∠AOP or ∠BOP or ∠AOQ or ∠BOQ, you will see that
∠AOP = ∠BOP = ∠AOQ = ∠BOQ = 90°
Also measure AO and OB, you will see that AO and OB are equal to each other.
Thus, it is verified that PQ is the perpendicular bisector of given line segment AB at point O.
Justification of Construction :
Join AP, AQ, BP and BQ.
In triangles PAQ and PBQ,
AP = BP
(Arcs of equal radii)
AQ = BQ
(Arcs of equal radii)
PQ = PQ (Common)
Therefore, ΔΡΑQ = ΔΡΒΟ (SSS rule)
So, ∠APO = ∠BPO (CPCT)
Now in triangles POA and POB,
AP = BP
PO = PO (Common)
∠APO = ∠BPO (Proved above)
Therefore, ΔΡΟΑ ≅ ΔΡΟΒ (SAS rule)
So, AO = BO … (i)
and ∠POA = ∠POB …(ii)
(CPCT)
As ∠POA + ∠POB = 180° (Linear pair axiom) … (iii) .
Therefore using (ii) and (iii), we get
∠POA = ∠OB = 90° …(iv)
Therefore, PO that is PQ is perpendicular bisector of AB.
[Using (i) and (iv)]
TEXT BOOK EXERCISE – 11.1
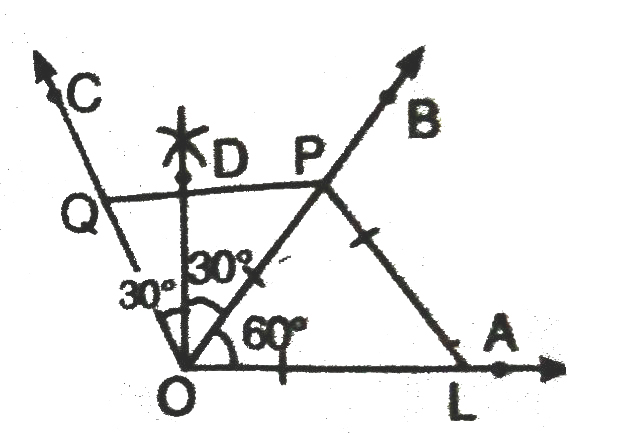
1. Construct an angle of 90° at the initial point of a given ray and justify the construction.
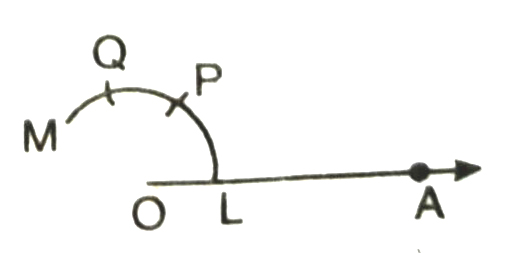
Steps of Construction :
1. Draw a ray OA.

2. With O as centre and convenient radius, draw an arc LM cutting OA at L.

3. Now with L as centre and radius OL, draw an arc cutting the arc LM at P.

4. Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.
5. Join OP to draw the ray OB. Also join O and Q to draw the ray OC. We observe that :
∠AOB = ∠BOC = 60º
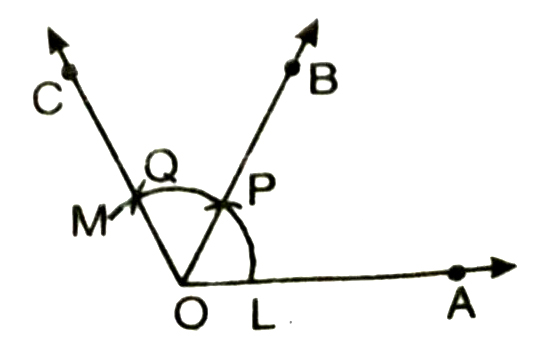
6. Now we have to bisect ∠BOC. For this; with P as centre and radius greater than 1/2 PQ draw an acr.
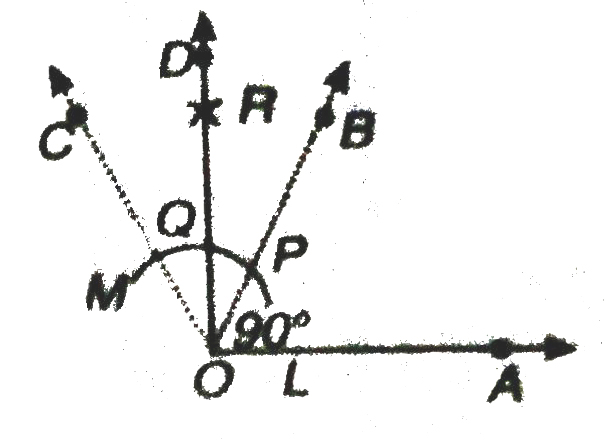
7. Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.
8. Join O and R and draw ray OD.
Then ∠AOD is the required angle of 90°.
Verification. Measure ∠AOD, you will see that ∠AOD = 90º.
Justification of construction :
Join PL, then
OL = OP PL (by construction)
Therefore ΔOPL is an equilateral triangle and ∠POL which is same as ∠BOA is equal to 60°.
Now join QP; then
OP = OQ = PQ
(by construction)
Therefore ΔOQP is an equilateral triangle
∴ ∠POQ which is same as ∠BOC is equal to 60º
By construction OD is bisector of ∠BOC
∴ ∠DOC = ∠DOB = 1/2 ∠BOC
= 1/2 × 60º = 30º
Now ∠DOA = ∠BOA + ∠DOB
⇒ ∠DOA = 60º + 30º
⇒ ∠DOA = 90º.
2. Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution :
Observe that 45º = 1/2 × 90º
We therefore follow the procedure of bisecting a given angle to get the required angle.
Thus to construct an angle of 45°, we proceed as follows :
Steps of Construction :
1. Draw ∠AOD = 90° (Note: follow the same steps as done in construction of angle 90°)
2. With L as centre and radius greater than 1/2 LS, draw an arc.
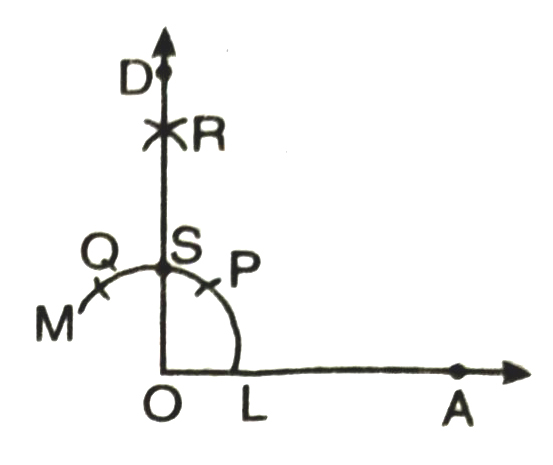
3. Now, with S as centre and the same radius as in step 2, draw another arc cutting the arc drawn in step 2 at T.
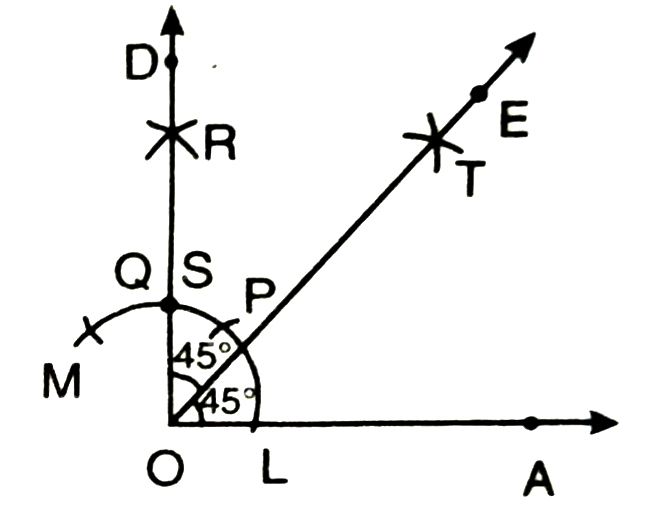
4. Join O and T and draw ray OE.
Thus, OE bisects ∠AOD and therefore ∠AOE = ∠DOE = 45°.
Verification. Measure ∠AOE, you will see that ∠AOE = 45°.
Justification of construction :
Join LS then AOLS is isosceles right triangle rt. angle at O.
∴ OL = OS
Therefore O lies on the perpendicular bisector of SL.
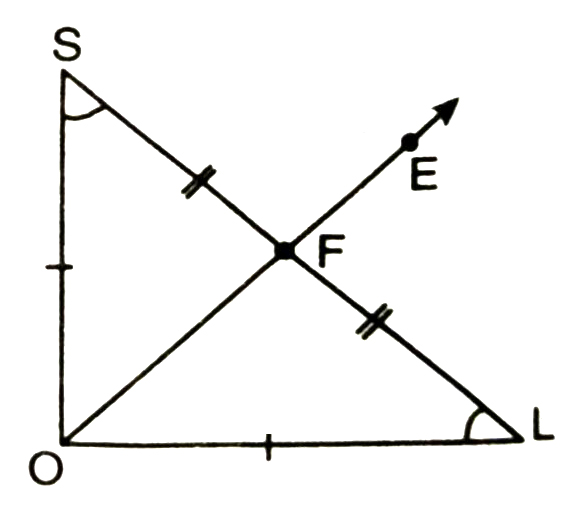
∴ SF = FL
and ∠OFS = ∠OFL (each 90°)
Now in ΔOFS and ΔOFL
OF = OF (Common)
OS = OL (By Construction)
SF = FL (Proved above)
∴ ΔOFS ≅ ΔOFL (By SSS rule)
⇒ ∠SOF = ∠LOF (CPCT)
Now
∠SOF + ∠LOF = ∠SOL
⇒ ∠LOF + ∠LOF = 90°
⇒ 2∠LOF = 90°
⇒ ∠LLOF = 1/2 × 90º
⇒ ∠LOF = 45°
or ∠AOE = 45°
(Which is true according to construction.)
3. Construct the angles of the following measurements.
(i) 30° (ii) 22-½° (iii) 15°.
Solution.— (i) Construction of 30°.
Observe that 30° = 1/2 × 60º
We therefore follow the procedure of bisecting a given angle learnt in construction to get the required angle.
Thus to construct an angle of 30°, we proceed as follows:
Steps of Construction :
1. Draw a ray OA.

2. With O as centre and a suitable radius, draw an arc LM that cuts OA at L.
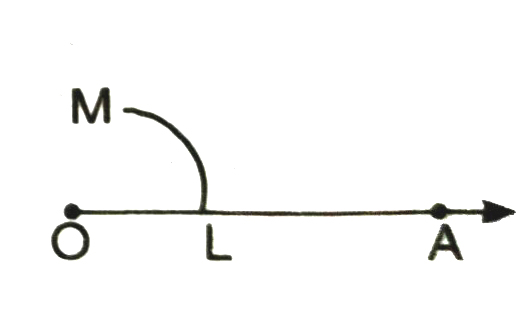
3. With L as centre and radius OL, draw an arc to cut LM at N.
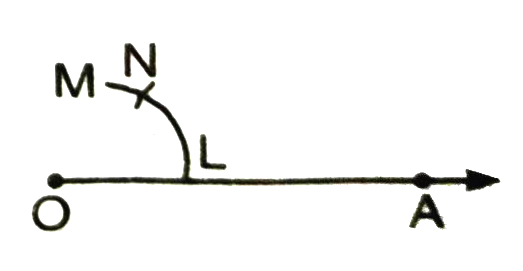
4. Join O and N draw ray OB. Then ZAOB = 60°.
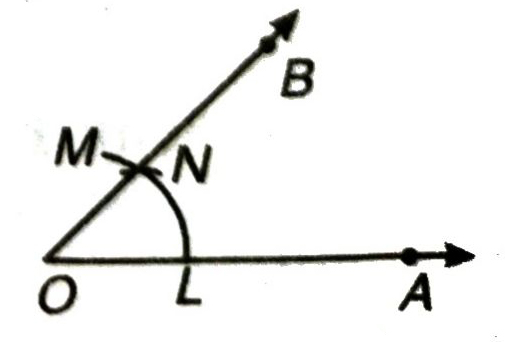
5. With L as centre and radius greater than 1/2 LN, draw an arc.
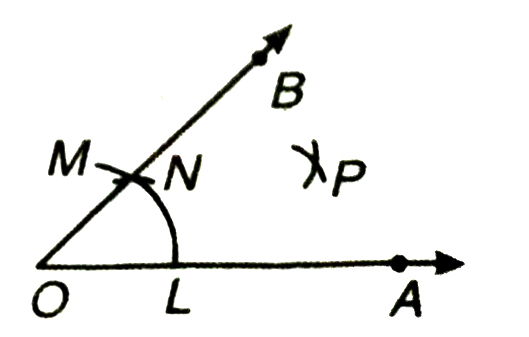
6. Now with N as centre and same radius as in step 5, draw another arc cutting the arc drawn in step 5 at P.
7. Join O and P and draw ray OC. 7.
Thus OC bisects ∠AOB and therefore
∠AOC = ∠BOC = 30°
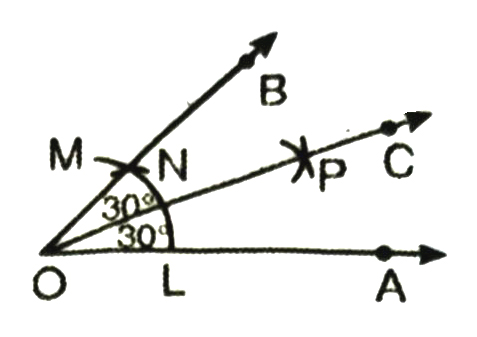
Verification. Measure ∠AOC, you will see that ∠AOC = 30°.
(ii) Construction of 22 1º/2
Observe that 22 1º/2 = 1/2 × x45⁰
We therefore follow the procedure of bisecting a given angle learnt in construction to get the required angle.
Thus to construct an angle of 221º/2 ; we proceed as follows :
Steps of Construction :
1. Draw ∠AOD = 90°
(Note: Follow the same steps as done in construction of 90° in Q. No. 1)
2. Now bisect ∠AOD by ray OE such that ∠DOE = ∠AOE = 45° (Note: Follow the same steps as done in construction of 45° in Q. No. 2.)
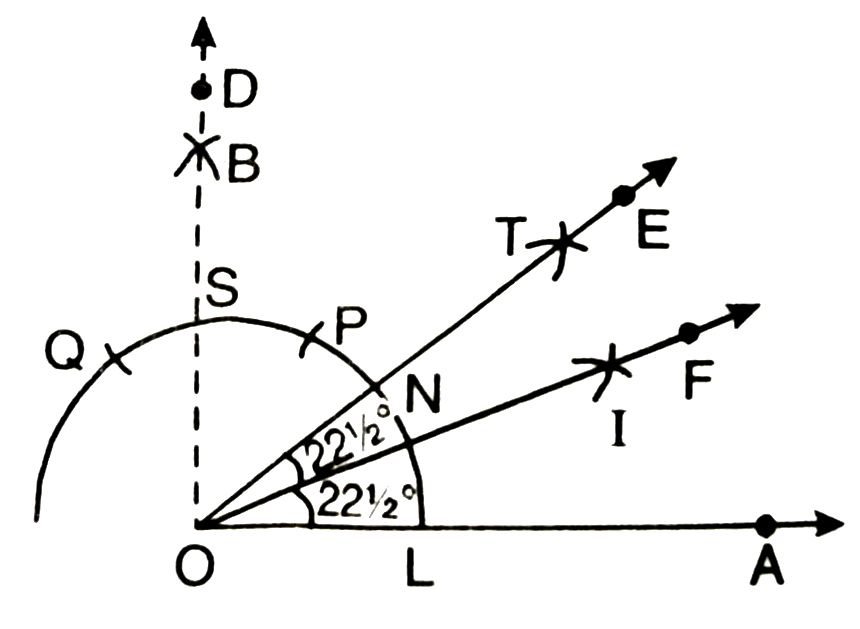
3. Let ray OE intesect the arc of circle at N.
4. Now with L as centre and radius greater than 1/2 LN, draw an arc.
5. With N as centre and same radius as in step 4, draw another arc cutting the arc drawn in step 4 at I.
6. Join O and I and draw ray OF. Thus OF bisects ∠AOE and therefore ∠AOF = ∠EOF = 22-1º/2
Verification. Measure ∠AOF with protractor. We observe that ∠AOF = 22-1º/2
(iii) Construction of 15°
Observe that 15° = 1/2 × 30º
We therefore follow the steps of bisecting a given angle learnt in construction to get the required angle.
Thus to construct an angle of 15°; we proceed as follows :
Steps of Construction :
1. Draw ∠AOB = 60°.
2. Now bisect ∠AOB by ray OC such that ∠BOC = ∠AOC = 30° [Note: Follow the same steps as done in construction of 30° in Q. No. 3 part (i).]
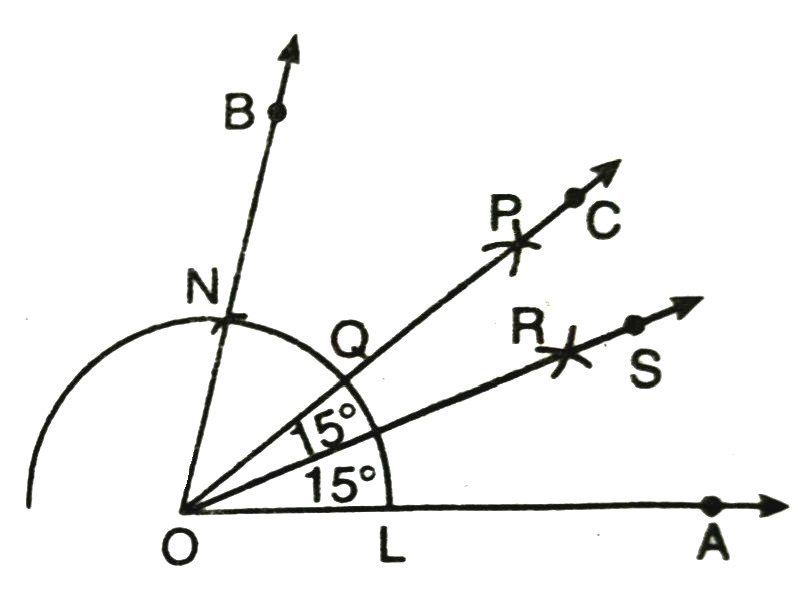
3. Let ray OC intersects the arc of circle at point Q.
4. Now with L as centre and radius greater than 1/2 LQ; draw an arc.
5. With Q as centre and same radius as in step 4; draw another arc cutting the arc drawn in step 4 at R.
6. Join O and R and draw ray OS.
Thus OS bisects ∠AOC and therefore ∠COS = ∠AOS = 15°
Verification. Measure ∠AOS with protractor. We observe that ∠AOS = 15⁰.
4. Construct the following angles and verify by measuring them by a protractor
(i) 75° (ii) 105° (iii) 135°
Solution.— (i) Construction of 75°
Steps of Construction :
1. Draw ∠ABE = 60° and ∠ABF = 90° (Note: Follow the same steps as done in Example 1 and question No. 1.)
2. Let ray BF intersects the arc of circle at G.
3. Now with M as centre and radius greater than 1/2 MG draw an arc.
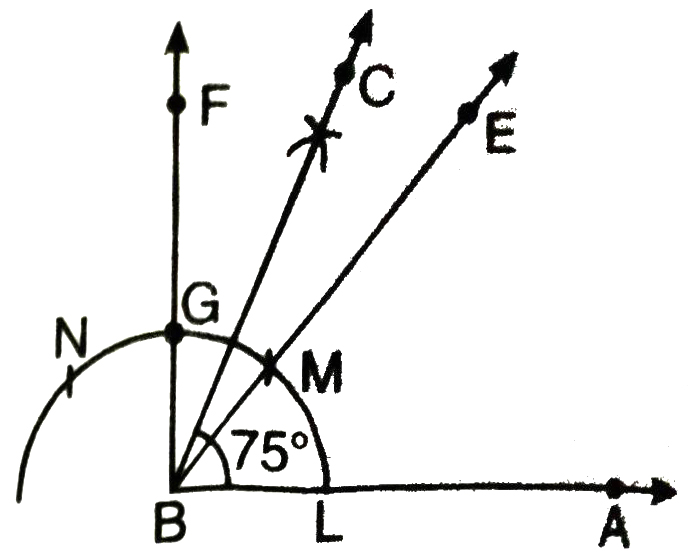
4. With G as centre and with same radius as in step 3; draw an arc which intersect the previous arc at point H.
5. Draw a ray BC passing through H which bisects ∠EBF.
Thus ∠ABC = 75° is the required angle.
Verification: Measure LABC with protractor. We observe that ∠ABC = 75°.
Justification of Construction :
∠EBF = ∠ABF – ∠ABE = 90° – 60° = 30°
∠EBC = ∠CBF
= 1/2 ∠EBF = 1/2 (30º)
[BC is the bisector of ZEBF]
∴ ∠ABC = ∠ABE + ∠EBC
= 60° + 15°
∠ABC = 75°
(Which is true when measured with protractor.)
(ii) Construction of 105°
Steps of Construction :
1. Draw ∠ABE = 90° and ∠ABF = 120°
2. Let ray BE intersects the arc of circle at M and ray BF intersect the arc of circle at N.
3. With M as centre and radius greater than 1/2 MN ; draw an arc.
4. With N as centre and with same radius as in step 3, draw another arc which intersect the previous arc at P.
5. Draw a ray BC passing through P which bisects ∠EBF.
Thus ∠ABC = 105° is the required angle.
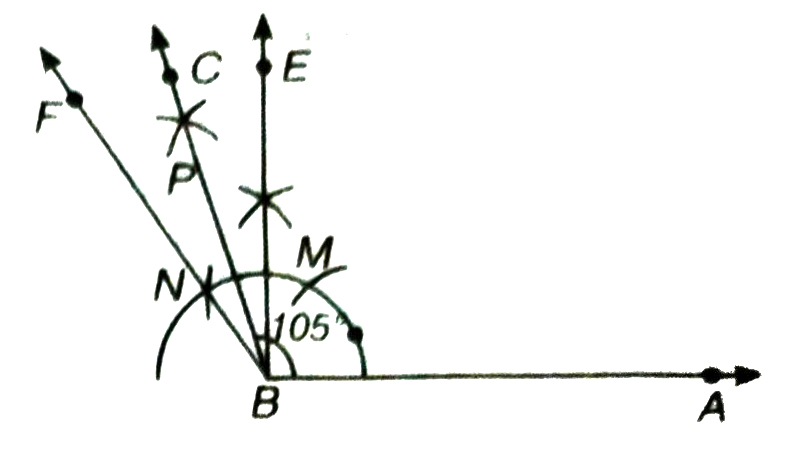
Verification : Measure ∠ABC with protractor. We observe that ∠ABC = 105°.
Justification of Construction :
∠EBF = ∠ABF – ∠ABE
⇒ ∠EBF = 120° – 90° = 30°
∠EBC = ∠CBF = 1/2 ∠EBF
= 1/2 (30º) = 15º [∴ BC is the bisector of ∠EBF]
∴ ∠ABC + ∠ABE + ∠EBC
= 90° + 15°
⇒ ∠ABC = 105°
[Which is true when measured with protractor.]
(iii) Construct of 135°.
Steps of Construction :
1. Draw a ray OA.

2. With O as centre and convenient radius, draw an arc LM (having length more than the semicircle) cutting OA at L.
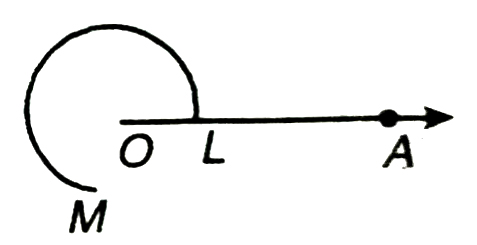
3. Now with L as centre and radius = OL; draw an arc cutting the arc LM at P.
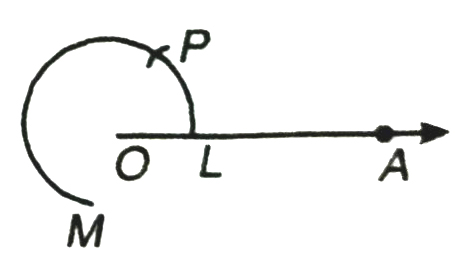
4. Then taking P as centre and radius OL, draw an arc cutting arc PM at Q.
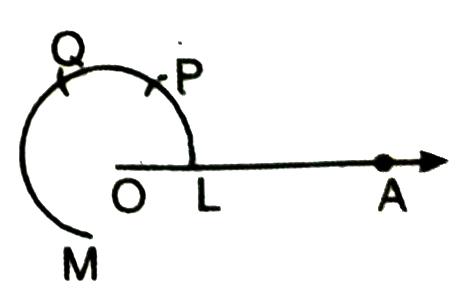
5. Now bisect ∠POQ by ray OB, we get ∠AOB = 90°.
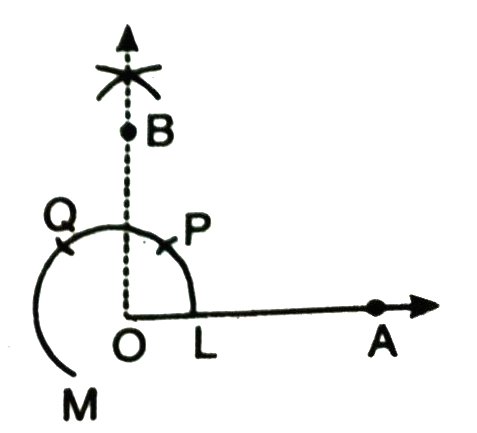
6. Now taking Q as centre and radius OL, draw an arc cutting QM at N.
7. Join O and N to draw the ray OC.
Thus, we get ∠AOC = 180°
or ∠BOC = ∠AOB = 90°
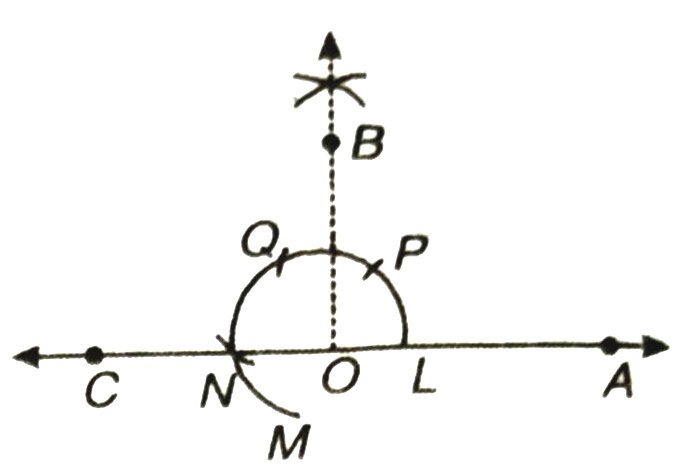
8. Now bisect ∠BOC by ray OD.
Then ∠AOD is the required angle of 135°.
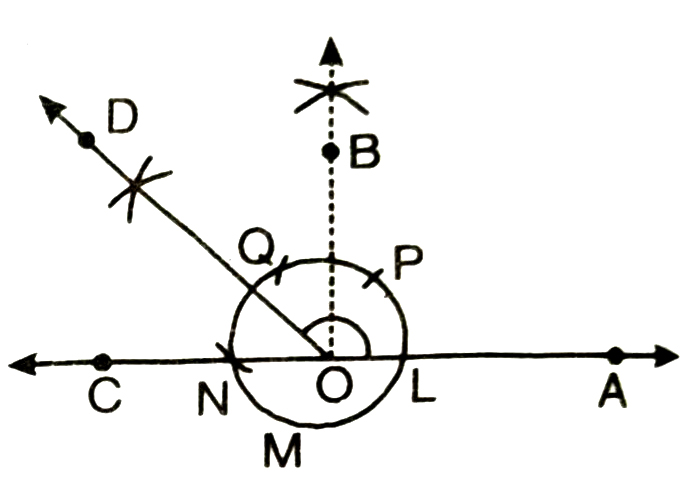
[ Because ∠AOD = ∠AOB + ∠BOD = 90° + 45° = 135°]
Verification. Measure ∠AOD by using protractor. You will see that ∠AOD = 135º.
5. Construct an equilateral triangle, given its side and justify the construction.
Solution.— Construction of an equilateral triangle of given side (Let it be AABC whose each side is 6 cm)
Steps of Construction :
1. Draw a line segment BC of length 6 cm.
2. At B draw ∠XBC = 60°.
3. Draw prependicular bisector PQ of line segment BC.
4. Let A and D be the points where PQ intersects the ray BX and side BC respectively
5. Join AC
Thus ABC is the required equilateral triangle.
Justification of Construction :
In rt. ΔADB and rt. ΔADC,
AD = AD (Common)
∠ADB = ∠ADC (each 90°)
(by construction)
BD = CD (By construction)
∴ ΔADB ≅ ADC
(By SAS rule of congruency)
∠B = ∠C = 60° (By CPCT)
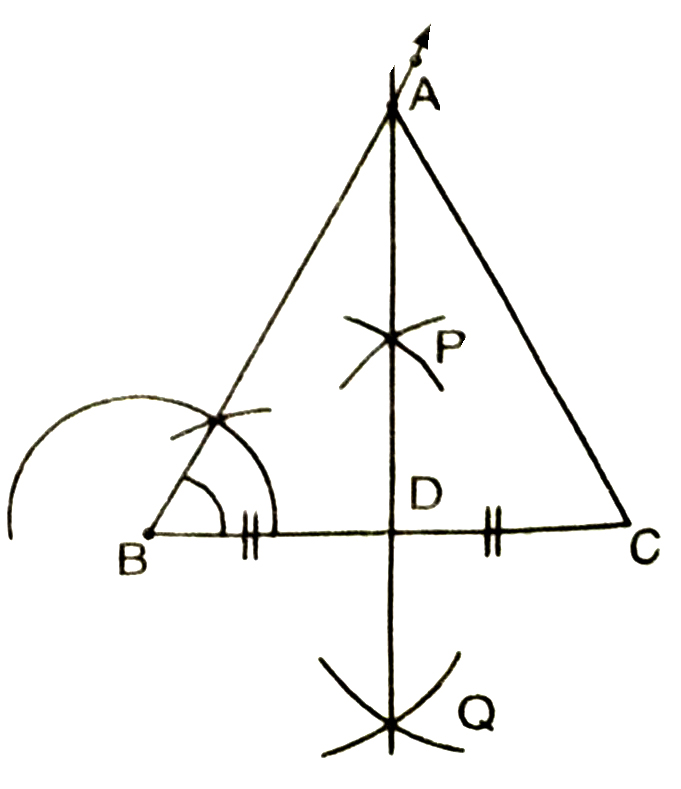
Therefore in ΔABC third angle;
∠A = 180° (∠B + ∠C)
= 180° – (60° + 60°)
= 180° – 120°
= 60°
Each of three angles of triangle is 60°.
Hence constructed triangle is an equilateral.
Some Constructions of Triangles.
So far some basic constructions have been considered. Next, some constructions of triangles will be done by using the constructions given in earlier classes and given above. Recall from the Chapter 7 that SAS, SSS, ASA and RHS rules give the congruency of two triangles. Therefore, a triangle is unique if
(i) two sides and the included
(ii) three sides are given, angle is given,
(iii) two angles and the included side is given and
(iv) in right triangle hypotenuse and one side is given.
You have already learnt how to construct such triangles in Class VII. Now let us consider some more constructions of triangles. You may have noted that at least three parts of a triangle have to be given for constructing it but not all combinations of three parts are sufficient for the purpose. For example, if two sides and an angle (not the included angle) are given then it is not always possible to construct such triangle uniquely.
Construction I :
To construct a triangle, given its base, sum of other two sides and one base angle.
Given : Base BC = a cm. AB + AC = x cm and ∠ABC = a of ΔABC.
Required : To construct the AABC
Steps of Construction :
1. Draw a ray BX and cut off a line segment BC = a cm from it.
2. At B, construct LXBY = a.
3. With B as centre and radius = x cm draw an arc to meet BY at D.

4. Join CD.
5. Draw the perpendicular bisector of CD intersecting BD at A.
6. Join AC. Then, ABC is the required triangle.
Note : AL is the perpendicular bisector of CD.
∴ AD = AC
Now BD = AB + AD
⇒ BD = AB + AC
AB + AC = x as described.
Construction II :
To construct triangle given its base, difference of the other two sides and one base angle.
Given : In ΔABC, BC = a cm,
∠ABC = a, AB – AC or AC – AB = d cm.
Required. To construct ΔABC.
Case (i) When AB > AC and AB – AC = d cm.
Steps of Construction :
1. Draw a ray BX and cut off a line segment BC = a cm.
2. At B, construct LXBY = a.
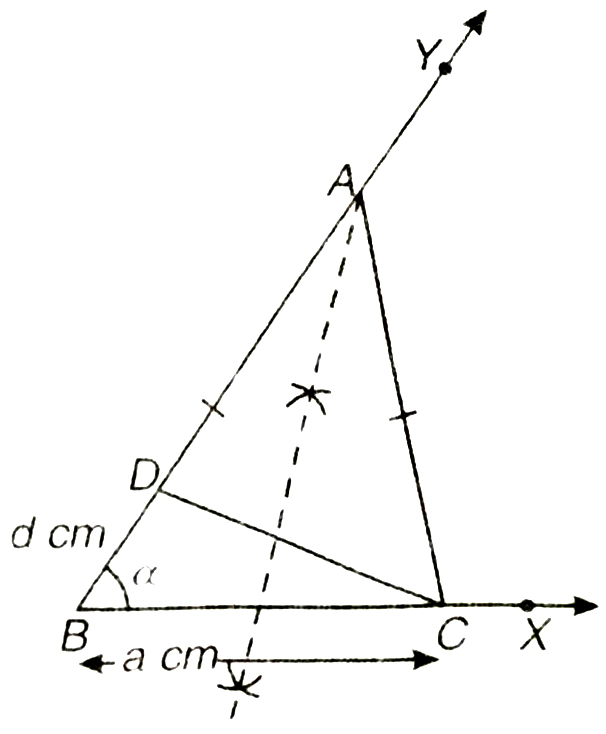
3. From BY, cut off BD = d cm.
4. Join CD.
5. Draw perpendicular bisector of CD intersecting BY at A.
6. Join AC. Then, ABC is the required triangle.
Case (ii) AB < AC and AC – AB = d cm.
1. Draw a ray BX and cut off a line segment BC = a cm.
2. Construct a ray BY making an angle a with BC and produce YB to form a line YBY’.
3. From BY’ cut off line BD’ = d cm.
4. Join CD’.
5. Draw perpendicular bisector of CD’ intersecting BY at point A.
6. Join AC. Then ABC is the required triangle.
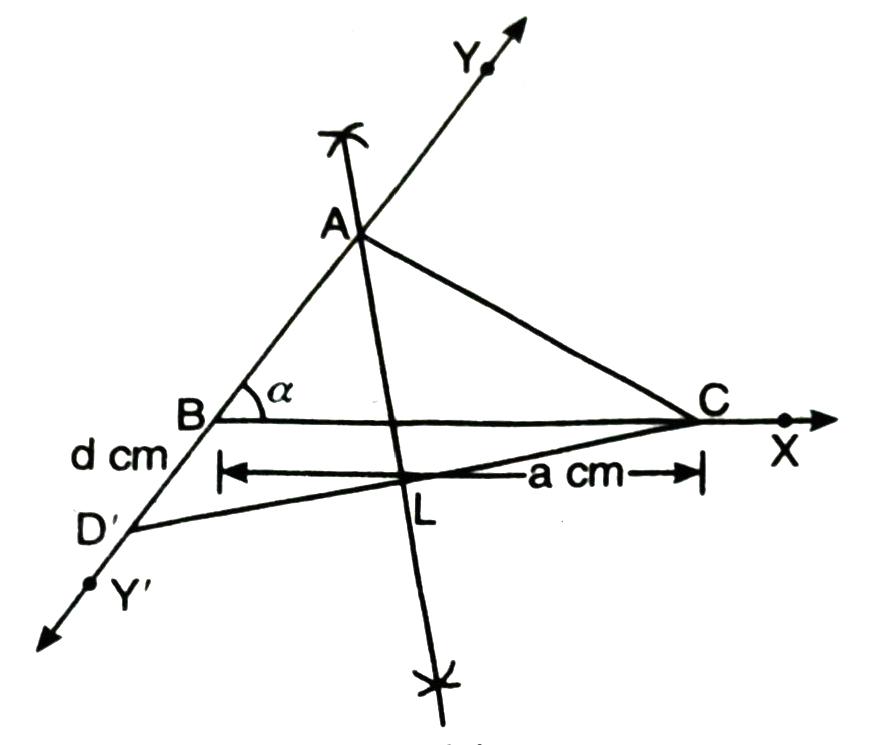
Note : Since AL is perpendicular bisector of CD’
∴ AD’ = AC
⇒ d + AB = AC
⇒ AC – AB = d as desired.
Construction III:
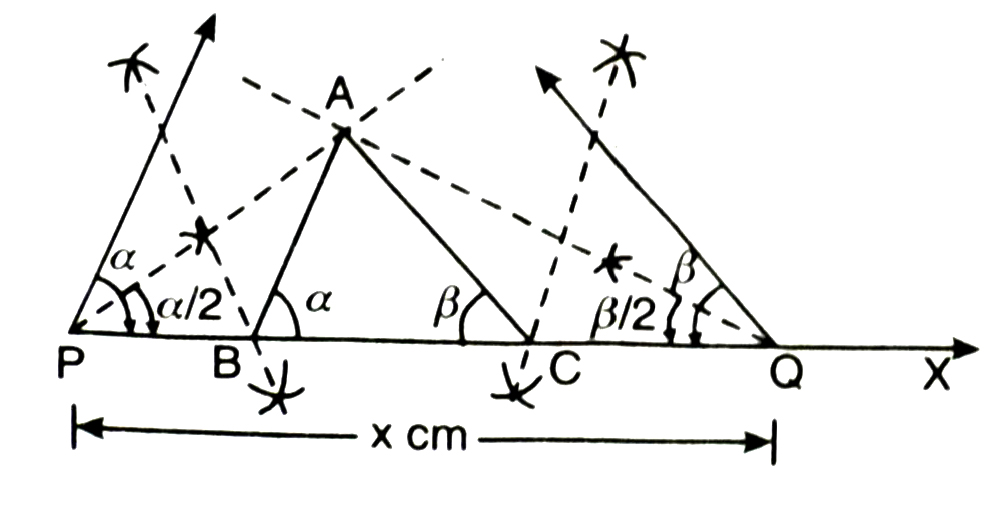
To construct a triangle when its perimeter and base angle are given.
Given. Perimeter of AABC i.e.,
AB + BC + CA = x cm. ∠ABC = a and ∠ACB = ß.
Required. To construct ΔABC.
Steps of Construction :
1. Draw a ray PX and cut off a line segment PQ = perimeter = x cm from it.
2. At P and Q construct angles equal to a and ß respectively.
3. Draw the bisectors of these angles meeting at a point A.
4. Draw the perpendicular bisectors of AP and AQ meeting PQ at B and C respectively.
5. Join AB and AC. Then ABC is the required triangle.
TEXT BOOK EXERCISE – 11.2
1. Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution.— Given : Base BC = 7 cm, ∠B = 75° and sum of two sides AB + AC = 13 cm.
Required : To construct ΔABC.
Steps of construction :
1. Draw a ray BX and cut off a line segment BC= 7 cm; from it.

2. At B; construct ∠YBX = 75°.
3. With B as centre and radius = 13 cm (: AB + AC = 13 cm) draw an arc to meet BY at D.
4. Join CD.
5. Draw perpendicular bisector PQ of CD intersecting BD at A.
6. Join AC.
Then ABC is the required triangle.
A lies on perpendicular bisector of CD.
∴ AC = AD and then
AB = BD – AD
AB = BD – AC
AB + AC = BD = 13 cm (which is true as given)
2. Construct a triangle ABC in which BC = 8 cm, ZB = 45° and AB-AC3-5 cm.
Solution.— Given : Base BC = 8 cm,
one base angle ∠B = 45°
and difference of two sides;
AB – AC 3.5 cm
Required : To construct ΔABC.
Steps of Construction :
1. Draw a ray BX and cut off a line segment BC = 8 cm from it.
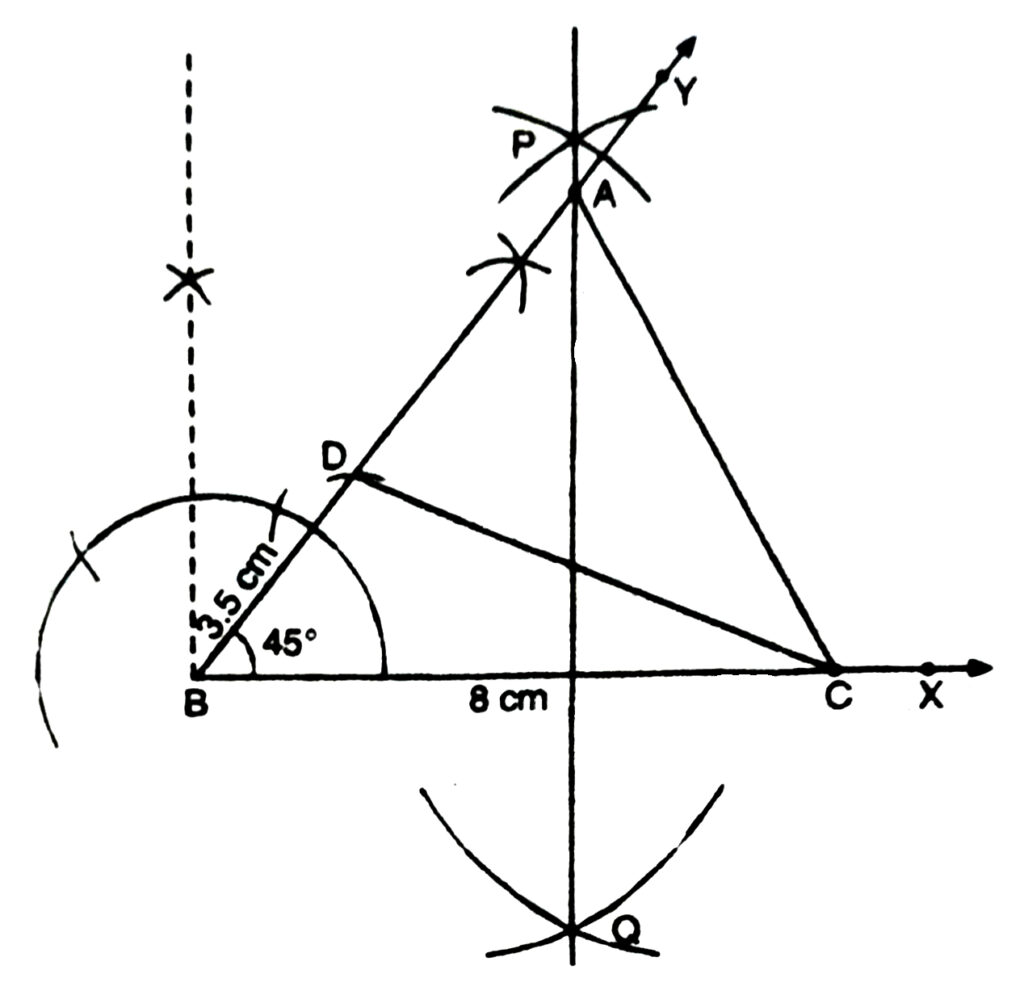
2. Cut ∠YBC = 45°.
3. Cut off a line segment BD = 3.5 cm
(∴ AB – AC = 3.5 cm) from BY.
4. Join CD.
5. Draw perpendicular bisector PQ of CD intersecting BY at a point A.
6. Join AC.
Then ABC is the required triangle.
A lies on the perpendicular bisector of CD.
∴ AD = AC
Now BD = AB – AD
⇒ BD = AB – AC
⇒ BD = AB – AC = 3.5 CM (which is true as given.)
3. Construct a triangle PQR in which QR = 6 cm, ZQ = 60° and PR-PQ = 2 cm.
Solution.— Given : Base QR = 6 cm; one base angle; ∠Q = 60° and difference of two sides;
PR – PQ = 2 cm
Required : To construct ΔPQR.
Steps of Construction :
1. Draw a ray QX and cut off a M line segment QR = 6 cm from it.
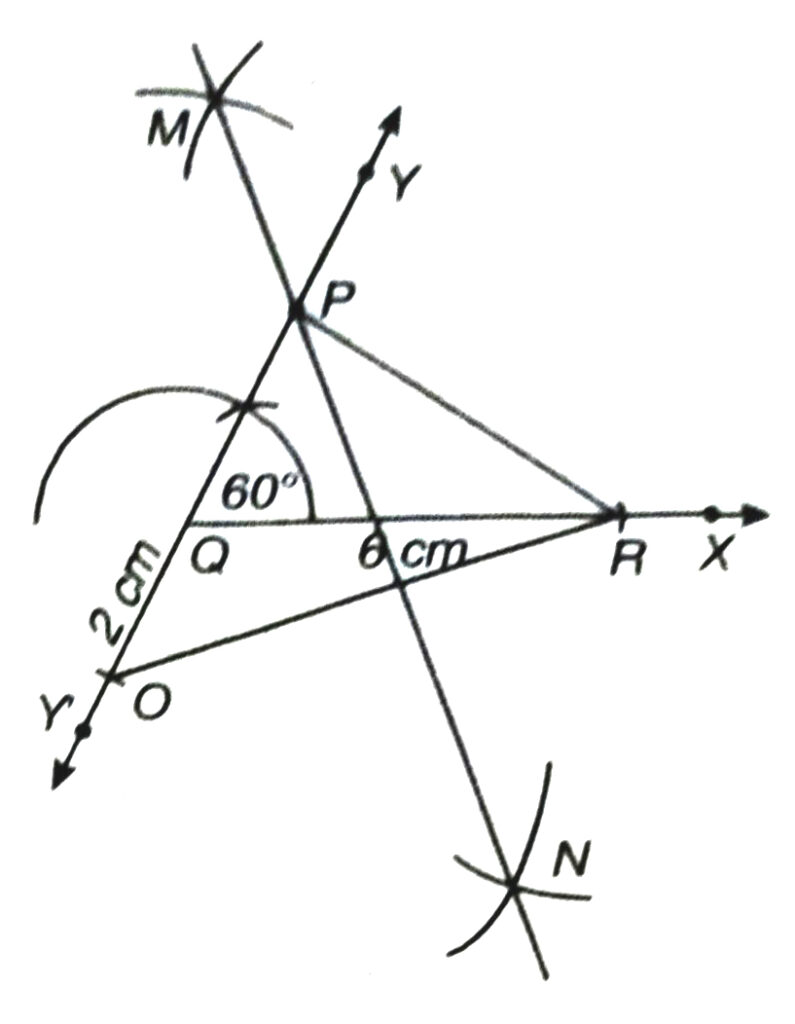
2. Construct a ray QY making an angle of 60° with QR and produce YQ to form a line YQY’.
3. Cut off a line segment QO = 2 cm
(∴ PR – PQ = 2 cm) from QY’.
4. Join OR.
5. Draw perpendicular bisector MN of OR.
6. Join PR.
Then PQR is the required triangle.
P lies on perpendicular bisector of OR.
∴ PO = PR
⇒ PQ + QO = PR
⇒ QO = PR – PQ
⇒ PR – PQ = 2 (which is true as given)
4. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Solution.— Given : Base angles; ZY = 30° and ZZ = 90°
Sum of three sides;
XY + YZ + ZX = 11 cm
Required : To construct ΔXYZ.
Steps of Construction :
1. Draw a line segment say PQ = 11 cm
(∴ XY + YZ + ZX = 11 cm).
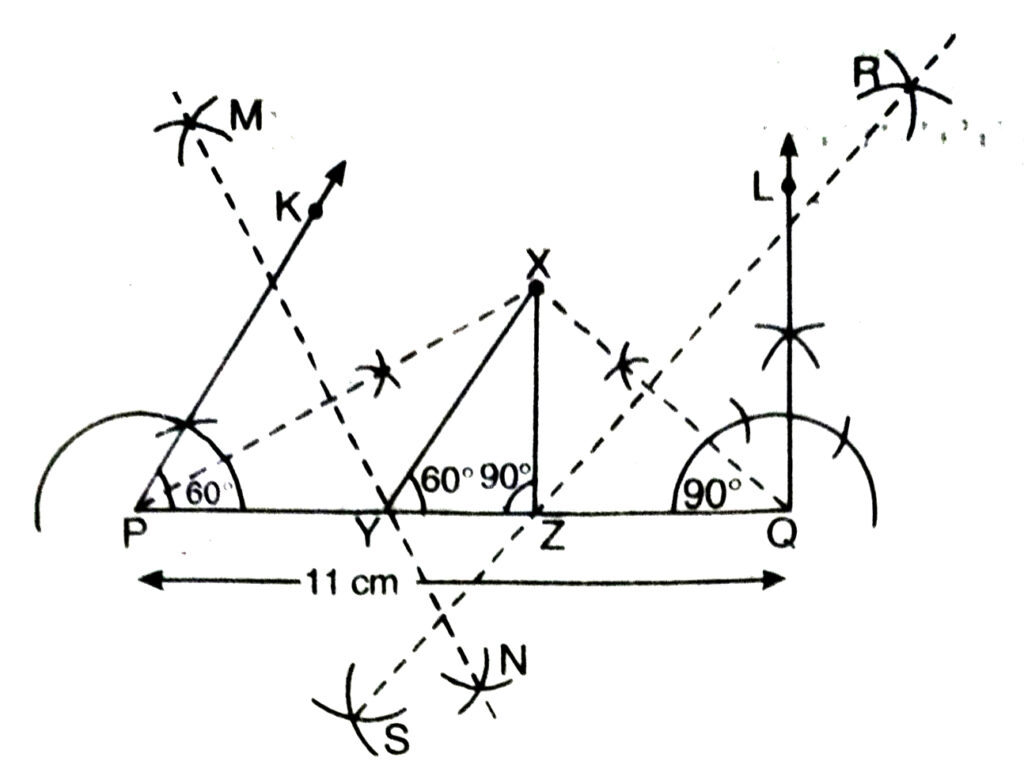
2. Draw ∠KPQ = 30° (∴ ∠Y = 30°)
and ∠LQP = 90° (∴ ∠Z = 90°).
3. Bisect the ZKPQ and ZLQP. Let these intersect at point X.
4. Draw perpendicular bisectors, MN of PX and RS of XQ.
5. Let MN intersect PQ at Y and RS intersect PQ at Z.
Join XY and XZ.
Then XYZ is the required triangle.
Justification for Construction :
We observe that Y lies on perpendicular bisector MN of PX.

5. Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution.— Let triangle to be constructed is ΔABC with base BC = 12 cm, the sum of its other side and hypotenuse
i.e. AB + AC = 18 cm
and ∠ABC = 90°
Steps of Construction :
1. Draw a ray BX and cut off a line segment BC = 12 cm from it.
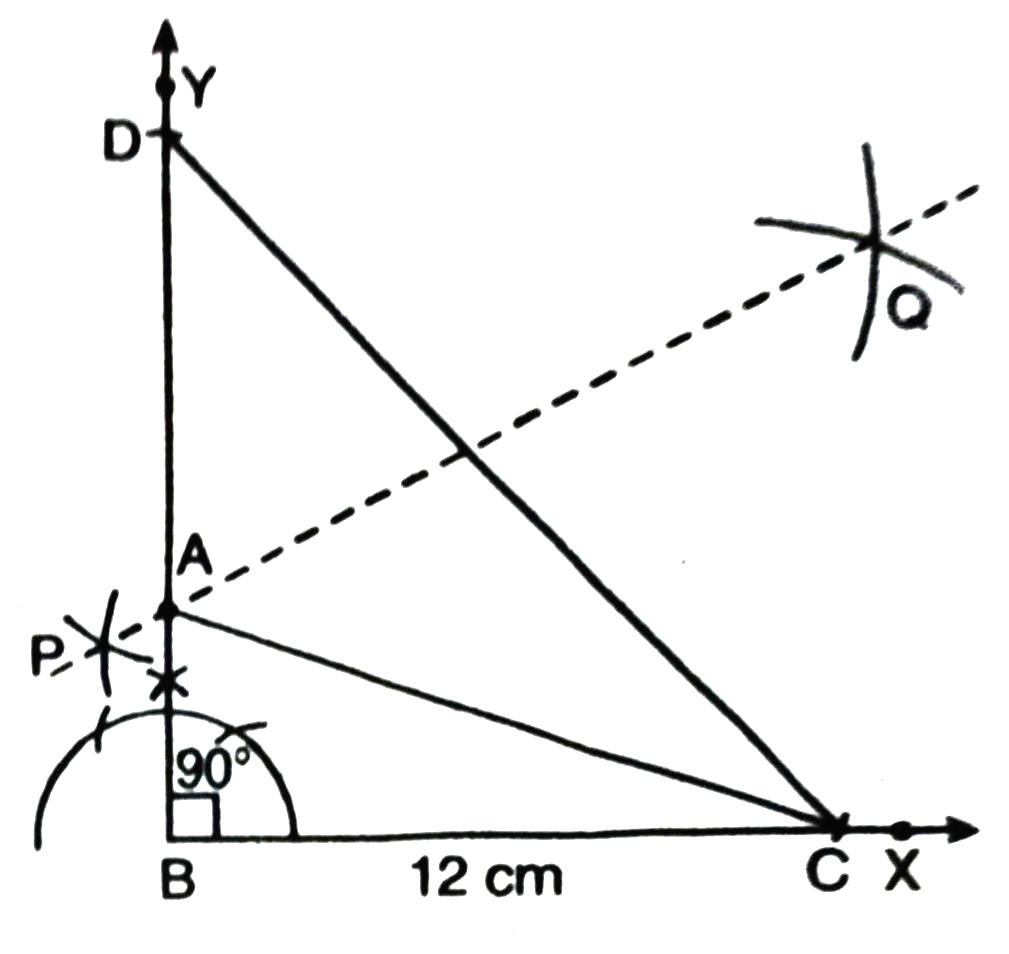
2. Construct ∠XBY = 90°.
3. From BY cut off a line segment BD = 18 cm.
4. Join CD.
5. Draw the perpendicular bisector of CD intersecting BD at A.
6. Join AC.
Then, ABC is the required right triangle.
A lies on the perpendicular bisector of CD.
∴ AC = AD and then
AB = BD – AD
⇒ AB = BD – AC
⇒ AB + AC = BD = 18 cm.
i.e. Sum of other side and hypotenuse is 18 cm (which is true as per given)
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here