JKBOSE 9th Class Mathematics Solutions Chapter 10 Circles
JKBOSE 9th Class Mathematics Solutions Chapter 10 Circles
JKBOSE 9th Class Mathematics Solutions Chapter 10 Circles
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Circles Textbook Questions and Answers
INTRODUCTION
You must have come across many objects whose shapes are circular, For example, wheels of vehicles, coins of many denominations used in different countries, utensils, watches and so on are all circular. The word ‘circular’ means ‘like a circle’ or ‘of the shape of a circle’. We shall discuss circles and some of their properties in this chapter.
Definition
A circle is a set of those points in a plane that are at a given constant distance from a given fixed point in the plane.
The fixed point is called the centre of the circle and the constant distance of every point on the circle from its centre is called the radius of the circle. Thus a circle is fully determined when its centre and radius are known. Circle can be defined as locus also.
If a point moves in a plane in such a manner that its distance from a given point in the plane remains constant, then the locus of the point is called a circle.
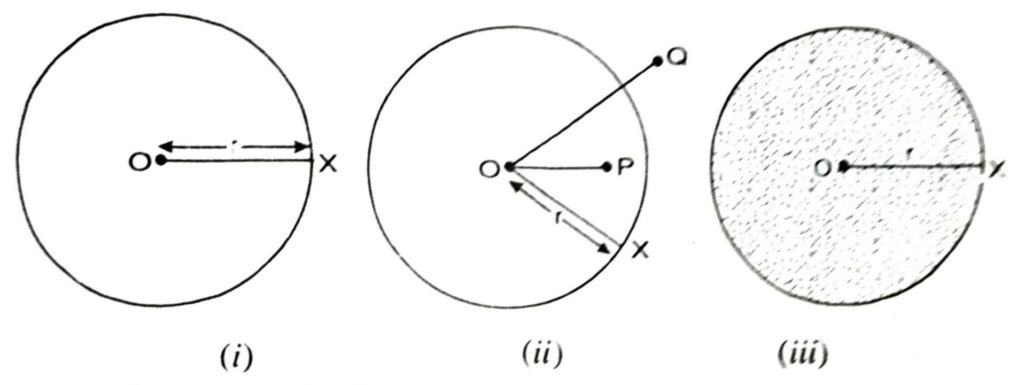
Hence onwards, all the figures and points considered and discussed will lie in a plane. We will not always mention that they lie in a plane. A circle with centre O and radius r is denoted by C(O, r) [See Fig. (i)]
In set notations we write
C(O, r) = {X : OX = r}
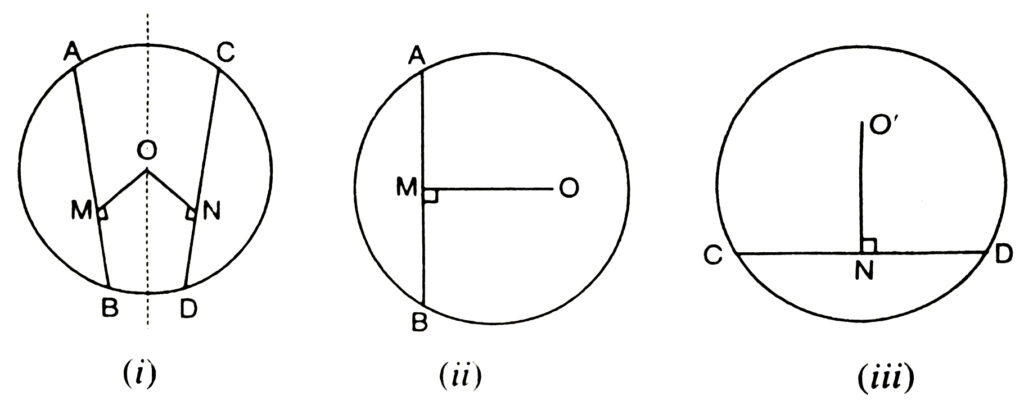
A point P such that OP <r, is said, to lie inside the circle, and a point Q such that OQ > r is to said to lie outside the circle [See Fig. (ii)]. The words ‘interior point’ and ‘exterior point’ are also used respectively to define points lying inside and outside of a circle. We may call the set of points lying inside and also on a circle C (O, r), a circular disc with centre O and radius r [See Fig. (iii)].
Circles having the same centre are said to be concentric circles [See Fig. (iv)].
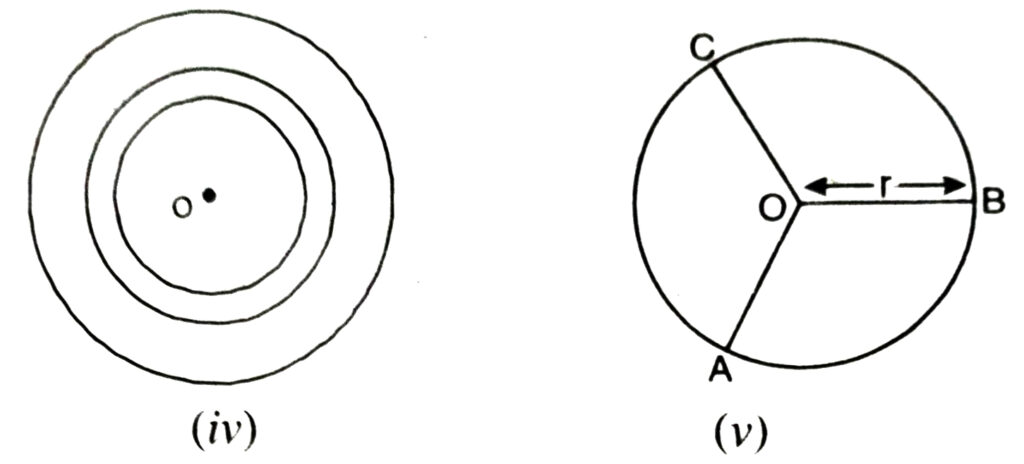
Remark : As you know, we have used the notation AB to denote the line segment AB and also its length. Similarly the word ‘radius’ will be used for a line segment joining the centre to any point on the circle and also for its length. Thus, in Fig. (v), OA, OB, OC are radii of the circle C(O, r).
Arc of a Circle.
A continuous piece of circle is called an arc. In Fig. (vi) the pieces P1P2, P3P4, P5P6, are all arcs of the circle C(O, r). If P, Q be any two points on a circle C(O, r), then the circle is divided into two pieces each of which is an arc. Now it will not be correct to denote both these arcs by PQ. We make use of the following convention to differentiate between these two arcs.
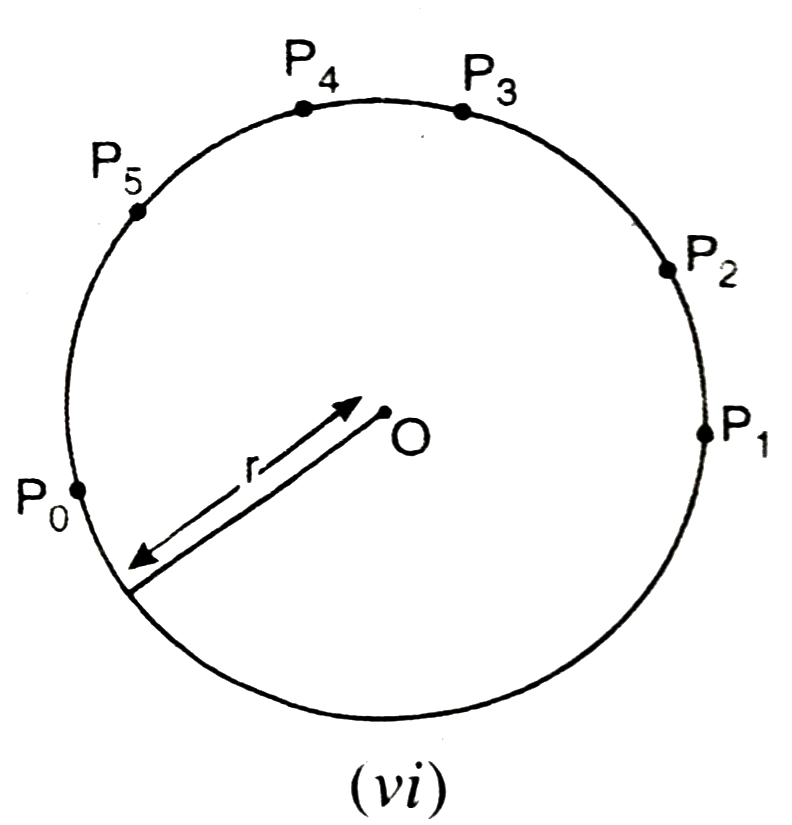
One end of the minute-hand in a clock completes a circle in one hour. This sense of description of the circle is called the clockwise direction. The opposite sense of description of the circle is called the counter clockwise direction.
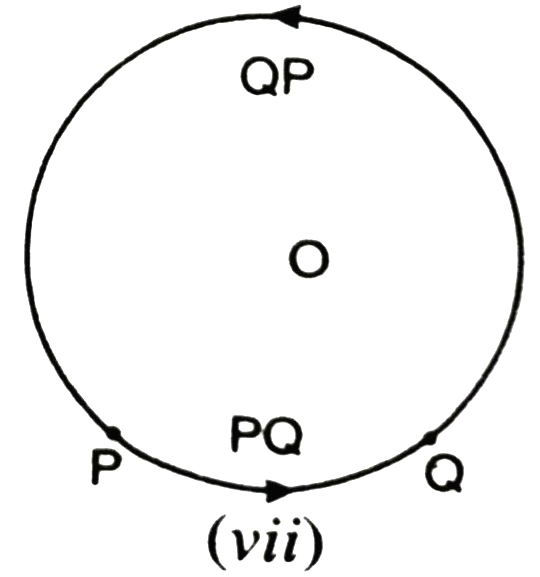
Now we denote the arc from P to Q in counter clockwise direction by PQ and one arc from Q to P in counter clockwise direction by QP [See Fig. (vii)]. Note that the points P and Q lie on the both PQ and QP.
An arc of a circle has a length but we shall not give here any precise method of finding this length. The length of an arc can be imagined to be equal to the length of a fine thread which covers the arc completely.
Using this intuitive idea it is clear that for any two points, P, Q on a circle either (i) l(PQ) > l(QP) or (ii) l(PQ) < l(QP) (iii) l (PQ) = l(QP), where (PQ) and l (QP) denote the lengths of PQ or and QP respectively. We may call the larger of the two arcs the ‘major arc’ and the smaller one the ‘minor arc’.
Chord of a Circle
A line segment joining two points on a circle is called a chord of the circle. Note that a chord is not a part of the circle. A chord passing through the centre of the circle is called a diameter of the circle. A circle has many diameters. It can be shown that a diameter of a given circle is one of the largest chords of the circle. As in the case of a radius, the word ‘diameter’ is used for a chord passing through the centre, and also for its length. If d is diameter of the circle C(O, r), then
d = 2r [See Fig. viii (a)]
It is then evident that all diameters of a circle are equal. A diameter divides the circle into two equal parts which are arcs. Each of the two arcs is called a semi-circle. In Fig. viii (a)

PQ and QP are semi-circles.
Segment of a Circle.
Let PQ be a chord of the circle C(O, r). Then PQ divides the region enclosed by the circle (i.e. the circular disc) into two parts. Each of the parts is called a segment of the circle. The segment containing the major arc is called the major segment and the segment containing the minor arc, the minor segment [Fig. viii (b)].

Though they are segments of a circular disc, they are called segments of a circle. Each of them is called the alternate segment of the other.
Congruence of Circles and Arcs
Two circles are said to be congruent if and only if one of them can be superposed on the other so as to cover it exactly.
Two circles C (O, r), and C (O’, s) are said to be congruent if r = 3, In words, we say that two circles are congruent if and only if they have equal radii.
Congruent arcs. Two arcs of a circle (or of congruent circles) are congruent if the degree measure of the two arcs are the same.
Thus arc AB ≅ arc CD if ∠AOB = ∠COD and ∠AOB = ∠COD ⇒ arc AB ≅ arc CD.
RESULTS TO REMEMBER
1. If two arcs of a circle (or of congruent circles) are congruent then the corresponding chords are equal.
2. If two chords of circle (or of congruent circles) are equal, then their corresponding arcs (minor, major or semi-circular) are congruent.
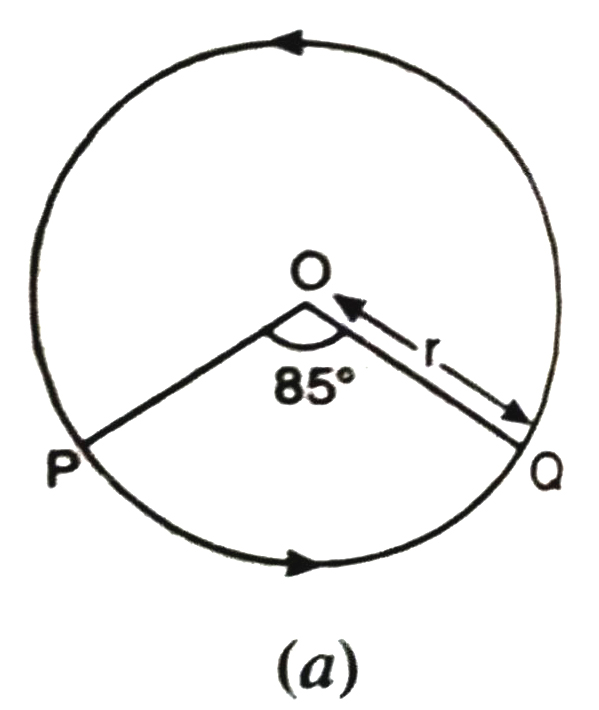
Degree measure of an arc. The degree measure of a minor arc is the measure of the central angle containing the arc.
Thus degree measure of semi-circle is 180°, the degree measure of a circle is 360° and the degree measure of a major arc is 360° minus the degree measure of the corresponding minor arc.
In Fig. (a), mPQ = 85°, mQP = 275°
and mPQ + mQP = 85° + 275° = 360°
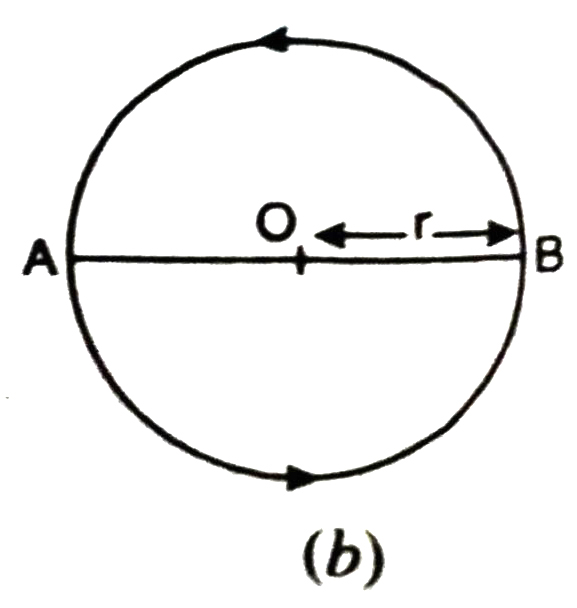
In Fig. (b), mAB = m BA = 180°
TEXT BOOK EXERCISE – 10.1
1. Fill in the blanks :
(i) The centre of a circle lies in …………. of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ……… of the circle.
(iii) The longest chord of a circle is a ……… of the circle.
(iv) An arc is a ……… when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and ………. of the circle.
(vi) A circle divides the plane, on which it lies, in ………. parts.
Solution.— (i) Interior
(ii) Exterior
(iii) Diameter
(iv) Semi-circle.
(v) Chord
(vi) Three.
2. Write True or False :
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs each is a major arc.
(iv) A chord, which is twice as long as its radius is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution.— (i) True
(ii) False
Correct Statement : A circle has infinite number of equal chords.
(iii) False
(iv) True
(v) False
Correct statement : Segment of a circle is the region between the chord and its corresponding arc.
(vi) True.
ANGLE SUBTENDED BY CHORD AT A POINT
Look at the Fig. (i); PQ is a chord of the circle with centre O, R is a point on the major arc PQ and S is a point on (minor) arc PQ. What are the angles POQ, PRQ and PSQ called ? ZPOQ is the angle subtended by the chord PQ, at the centre O and ZPRQ, ZPSQ are the angles subtended by PQ at points R and S on major and minor arcs PO respectively.
Let us examine the relationship between the size of the chord and angle subtended by it at the centre. You may see by drawing different chords of a circle and angles subtended by them at the centre that larger is the chord, bigger will be the angle subtended at the centre. What will happen if you take two equal chords of a circle ? Will the angles subtended at the centre be same or not ?
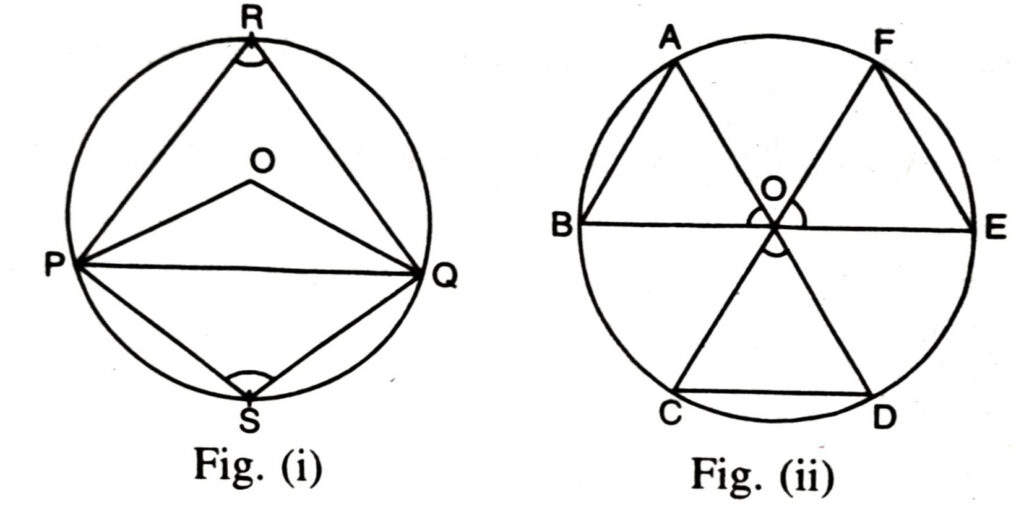
Draw two or more equal chords of a circle and measure the angles subtended by them at the centre (See Fig. (ii)). You will find that the angles are equal. Let us give the logical proof of this fact.
Theorem 1. Equal chords of a circle subtend equal angles at the centre.
Given : Two equal chords AB and CD of a circle with centre O (See Fig.)
To prove : ∠AOB = ∠COD.
Proof : In triangles AOB and COD, OA = OC (Radii of the circle)
OB = OD (Radii of the circle)
AB = CD (Given)
Therefore, ΔAOB = ΔCOD (By SSS rule of congruency)
Thus we get; ∠AOB = ∠COD
(Congruent parts of congruent triangles)

Theorem 2. If the angles subtended by the chords of a circle at the centre of the circle are equal, then the chords are equal.
The above theorem is the converse of the theorem 1. You can prove it also as follows.

TEXT BOOK EXERCISE – 10.2
1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution.— Two circles are said to be congruent if and only if one of them can be superposed on the other so as to cover it exactly.
Let C(O, r) and C(O’, s) be two circles. Let us imagine that the circle C(O’, s) is superposed on C(O, r) so that O’ coincide with O. Then it can easily be seen that C(O’, s) will cover C(O, r) completely if and only if r = s.
Hence we can say that two circle are congruent, if and only if, they have equal radii.
Now using this concept we have to prove that equal chords of congruent circles subtended equal angles at the centre which is proved as follows:
Given : PQ and RS are equal chords of congruent circles

C (O, r) and C'(O’ r).
To prove : ∠POQ = ∠ROS
Proof. In triangles POQ and ROS,
(See Fig.)
OP = OQ = OR = OS
= r (radius)
PQ = RS (given)
∴ ΔPOQ ≅ ΔROS (SSS rule of congruency)
∴ ∠POQ = ∠ROS (congruent part of congruent triangles)
2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution.—
Given : Two chords PQ and RS of congruent circles C(O, r) and C'(O’, r) such that.
∠POQ = ∠ROS
To prove : PQ = RS
Proof : In triangle POQ and ROS (see Fig.)

OP = OQ = OR = OS = r (radius)
∠POQ = ∠ROS (given)
∴ ΔPOQ ≅ ΔROS (SAS rule of congruency)
∴ PQ = RS (Congruent parts of congruent triangles)
PERPENDICULAR FROM CENTRE TO A CHORD
Trace a circle on a tracing paper. Let O be its centre. Draw a chord AB. Fold the paper along a line through O so that a portion of the chord falls on the other. Let the crease cuts AB at t3he point M. Then, ∠OMA = ∠OMB = 90° or OM is perpendicular to AB. Does the point B coincide with A ? (See Fig.)
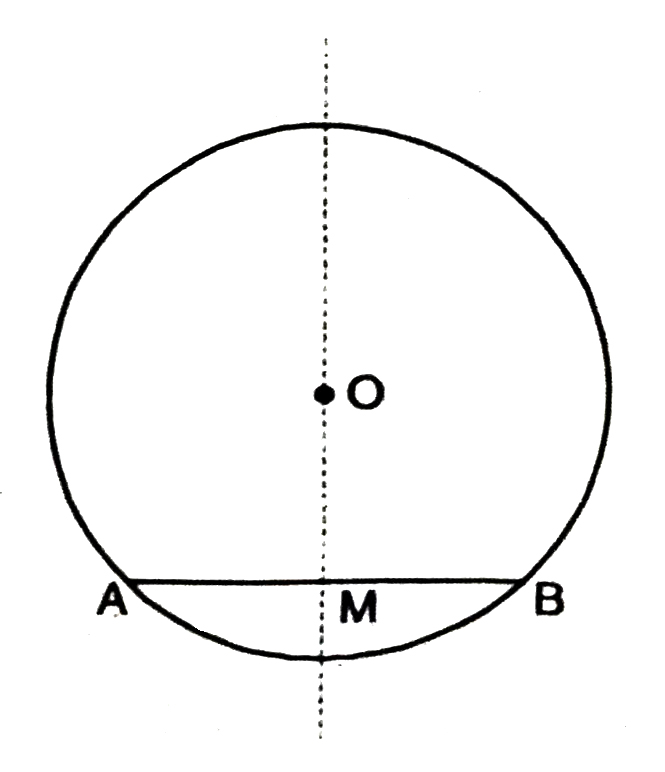
Yes, it will. So MA = MB. Give a proof yourself by joining OA and OB and proving the right triangles OMA and OMB to be congruent.
Theorem 3 : The perpendicular from the centre of a circle to a chord bisects the chord.

Theorem 4 : (Converse of Theorem 3)
The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.

Theorem 5. There is one and only one circle passing through three non-collinear points.
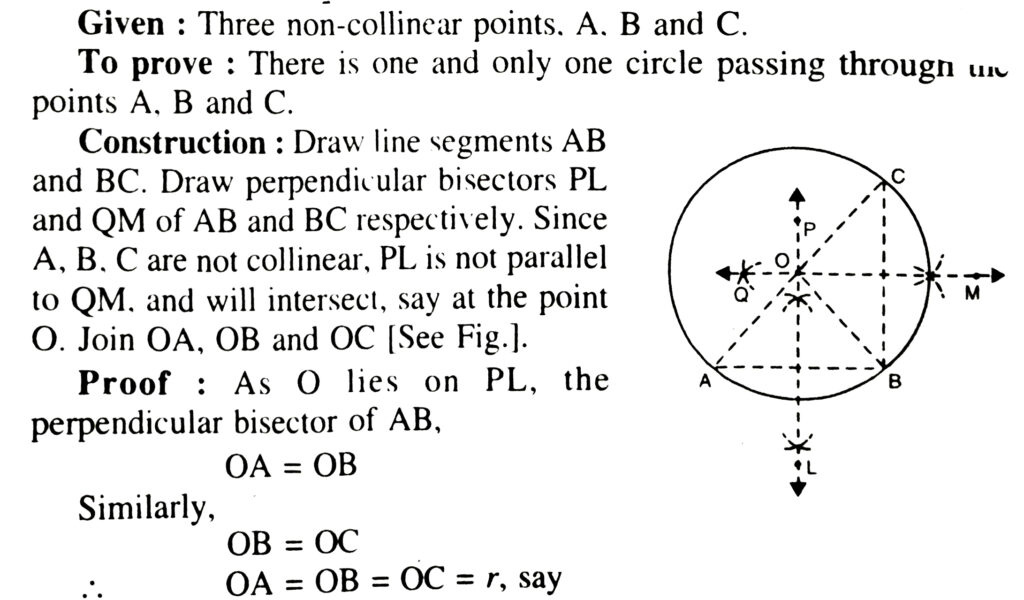
Taking O as centre and r the radius, draw a circle C(O, r) which will pass through A, B and C. This proves that there is a circle passing through the points A, B and C. We shall now prove that this is the only such circle. If possible, suppose that there be another circle C(O’, s) passing through A, B and C. Then O’ will lie on perpendicular bisectors PL of AB and QM of BC. Since two lines cannot intersect at more than one point. O’ must coincide with O. Since OA = r, O’ A = s, we have r = s. Hence C(O’, s) = C(O, r).
It follows immediately from Theorem 5 that there is a unique circle passing through the three vertices A, B, C of a AABC. This circle is called the circumcircle of the triangle ABC and its centre the circumcentre of the triangle.
TEXT BOOK EXERCISE – 10.3
1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points ?
Solution.— From the fig., we observe that when different pair of circles are drawn; each pair have two points (say A and B) in common.
Maximum number of common points are two in number.
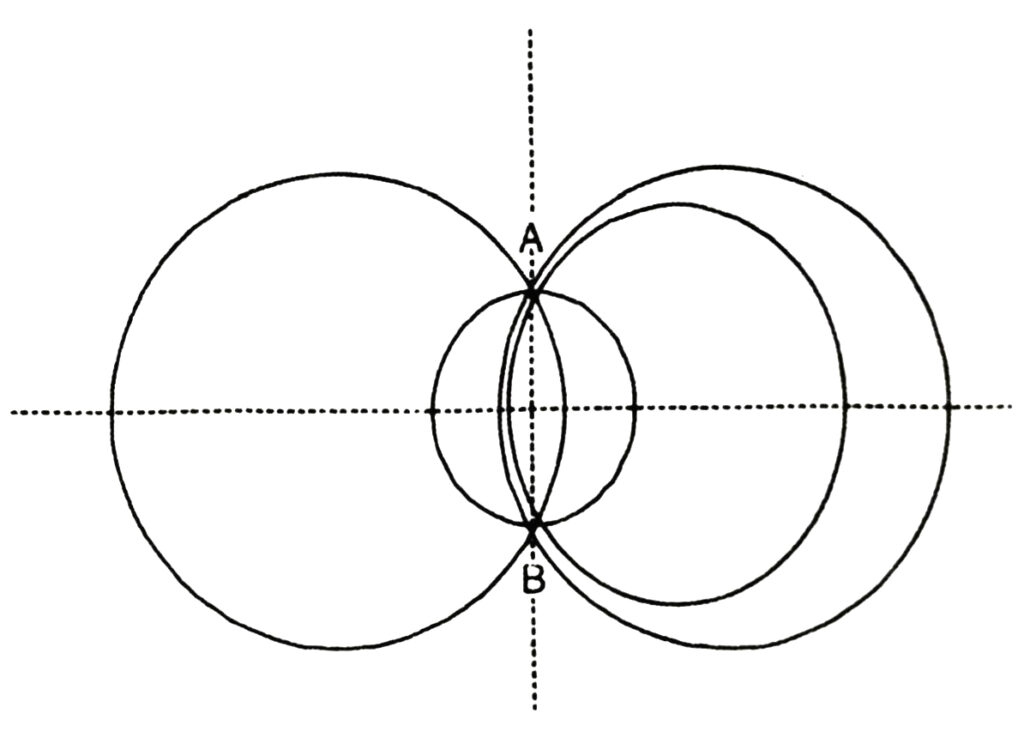
Suppose that two circles C(O, r) and C(O’, s) intersect each other in three points, say A, B and C.
Then A, B and C are non-collinear points. We know that :
There is one and only one circle passing through three non-collinear points.
Therefore a unique circle passes through A, B and C.
⇒ 0′ coincides with O and s = r

A contradiction to the fact that
C(O’, s) ≠ C(O, r)
∴ Our supposition is wrong.
Hence two different circles cannot intersect each other at more than two points.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution.—
Steps of Construction :
1. Take any three points A, B and C on the circle.
2. Join AB and BC.
3. Draw perpendicular bisector say LM of AB.
4. Draw perpendicular bisector PQ of BC.
5. Let LM and PQ intersect at the point O.
Then O is the centre of the circle.
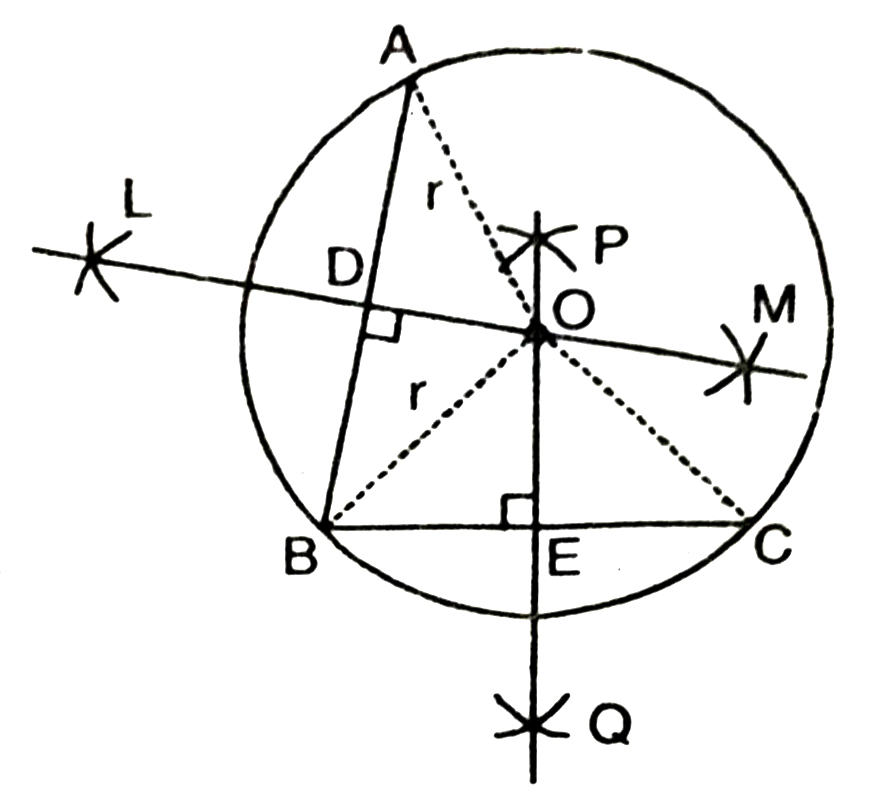
Verification :
O lies on the perpendicular bisector of AB.
∴ OA = OB …(i)
O lies on the perpendicular bisector of BC.
∴ OB = OC …(ii)
From (i) and (ii) we observe that
OA = OB = OC = r (say)
Three non collinear points A, B and C are at equal distance (r) from the point O inside the circle.
Hence O is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
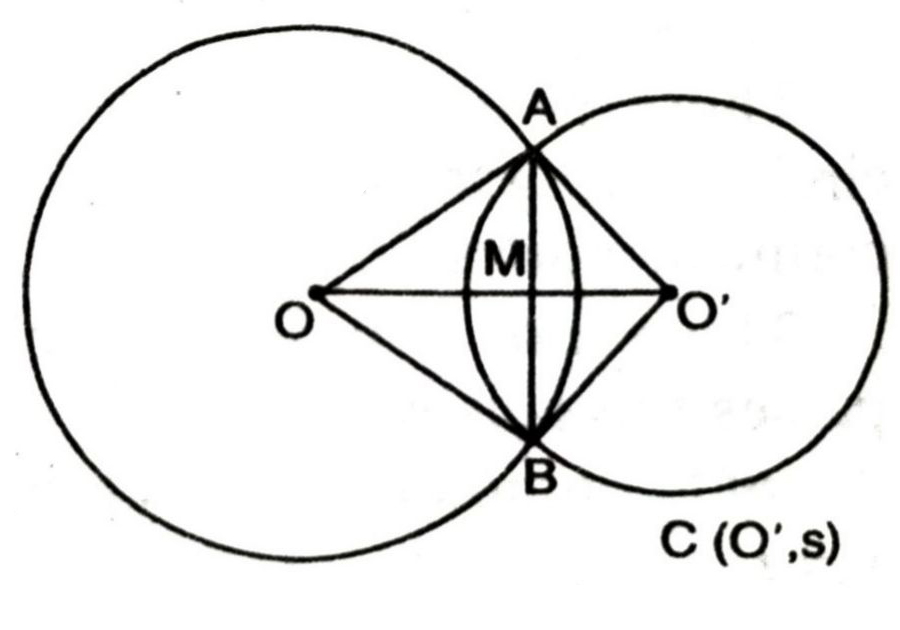
Proof. C(O, r) and C(O’, s) be two circles intersecting A and B. To prove 00′ is the perpendicular bisector of the C (0,chord AB. Draw line segments OA, OB, O’A and O’B (See Fig.)
In triangles OAO’ and OBO’,
OA = OB = R
O’A =O’B = S
and OO’ = OO’
∴ Δ OAO’ ≅ ΔOBO’ (SSS)
∴ ∠AOO’ = ∠BOO’
Let M be the point of intersection of AB and OO’. Then in triangles AOM and BOM,
OA = OB
∠AOM = ∠BOM
(∴ ∠AOO, = ∠AOM and ∠BOO’ = ∠BOM)
and OM = OM
∴ ΔAOM ≅ ΔBOM (SAS axiom)
∴ AM = MB …(i)
and ∠AMO + ∠BOM = 180º …(ii)
Now ∠AMO + ∠BMO (linear pair axiom)
⇒ ∠AMO + ∠AMO = 180º
⇒ 2∠AMO = 180º
⇒ ∠AMO = 180º/2
⇒ ∠AMO = 90º
also ∠BMO = 90º (∴ ∠AMO = ∠BMO)
Now we have
AM = MB
∠AMO = ∠BMO = 90º
It proves that line OO’ joining centres O and O’ lies on the perpendicular bisector of common chord AB.
Equal Chords and Their Distances from the Centre
A circle can have infinitely many chords. You may observe by drawing chords of a circle that bigger chord is nearer to the centre than the smaller chord. The diameter, being biggest chord, is at zero distance from the centre because the centre lies on it. You may think that there should be some relationship between the length of chords and their distances from the centre.
Draw a circle of any radius on a tracing paper. Draw two equal chords AB and CD of it and also the perpendicular OM and ON on them from the centre O. Fold the figure so that D falls on B and C falls
on A (See Fig. (i)), You may observe that O lies on the crease and N falls on M. Therefore, OM ON. Repeat the activity by drawing congruent circles with centre O and O’ and taking equal chords AB and CD one of each. Draw perpendiculars OM and O’N on them (See Fig. (ii) and (iii)). Cut one circle and put it on the other so that AB coincides with CD. Then you find that O coincides with O’ and M coincides with N. This way you verified the following :
Theorem 6. Equal chords of a circle (or of congruent circles) are equidistant from the centre (or corresponding centres).
We shall prove the theorem for two congruent circles. The proof for one circle will be similar.
Given : Chords PQ of circle C(O, r) and RS of circle C(O’, r) such that PQ = RS
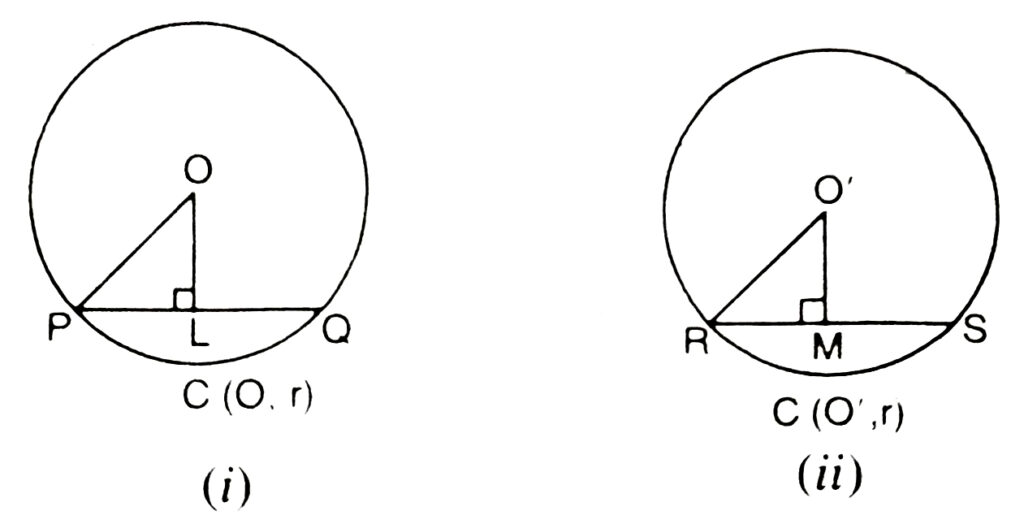
To prove : OL = O’M, where L, M are respectively the feet of perpendicular from O on PQ and from O’ on RS.
Construction : Draw line segment OP and O’R (See Fig. (i) and (ii))
Proof : As we know that perpendicular from the centre of the circle bisects the chord
∴ PL = LQ and RM = MS
In two right triangles OLP and O’MR
PL = 1/2 PQ = 1/2 RS = RM
OP = O’R = r
∴ ΔOLP ≅ ΔO’MR (RHS Theorem)
Hence OL = O’M (Congruent part of Congruent triangles)
Theorem 7. Chords of a circle (or of congruent circles), which are equidistant from the centre (or from the corresponding centres) are equal.
We shall prove, again, the theorem for two congruent circles and the proof for one circle will follow on the same lines.
Given : Chords PQ of a circle C (0, r) and RS of another congruent circle C(O’, r) such that OL = O’M, where L, M are respectively the feet of perpendiculars from O and PQ and from O’ on RS.
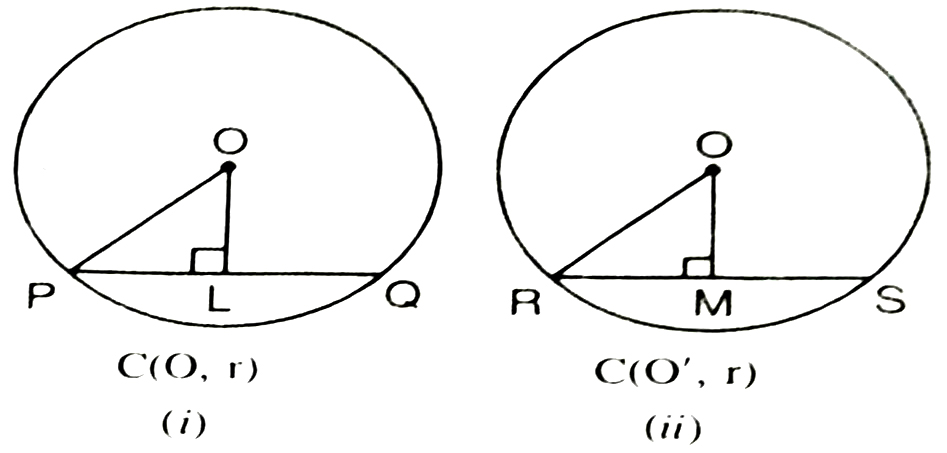
To Prove : PQ = RS
Construction : Join OP and O’R (See Figs. (i) and (ii)).
Proof : In the two right triangles OLP and O’MR,
OP = O’R = R
OL = O’M (given)
∴ ΔOLP ≅ ΔO’MR (RHS Theorem)
∴ PL = RM
Since L, M respectively are mid-points of PQ and RS by Theorem 3
∴ PQ = RS
TEXT BOOK EXERCISE – 10.4
1. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution.— Let two circles with centres O and O’ intersect each other at points A and B. On joining A and B ; AB is the common chord.
Radius OA = 5 cm, Radius O’A = 3 cm, Distance between their centres OO’ = 4 cm.
We observe that in triangle AOO’;
5² = 4² +3²
⇒ 25 = 16 + 9
⇒ 25 = 25
Pythagoras result, holds in ΔAO’O,
Hence, AAO’O is rt. ∠d triangle, rt. angle at O’.

As we know that perpendicular drawn from the centre of the circle bisects the chord.
Hence O’ is the mid-point of the chord AB. Also O’ is the centre of the circle II.
Therefore, length of chord AB = Diameter of circle II
∴ length of chord AB = 2 × 3 cm = 6 cm.
ALTER
Let two circles with centre O and O’ intersect each other at points A and B. Let common chord AB intersects OO at point C.
Let OC = x cm
∴ O’C = 4 – x cm

As we know that line joining the centres of two circles is perpendicular bisector of the common chord of circles.

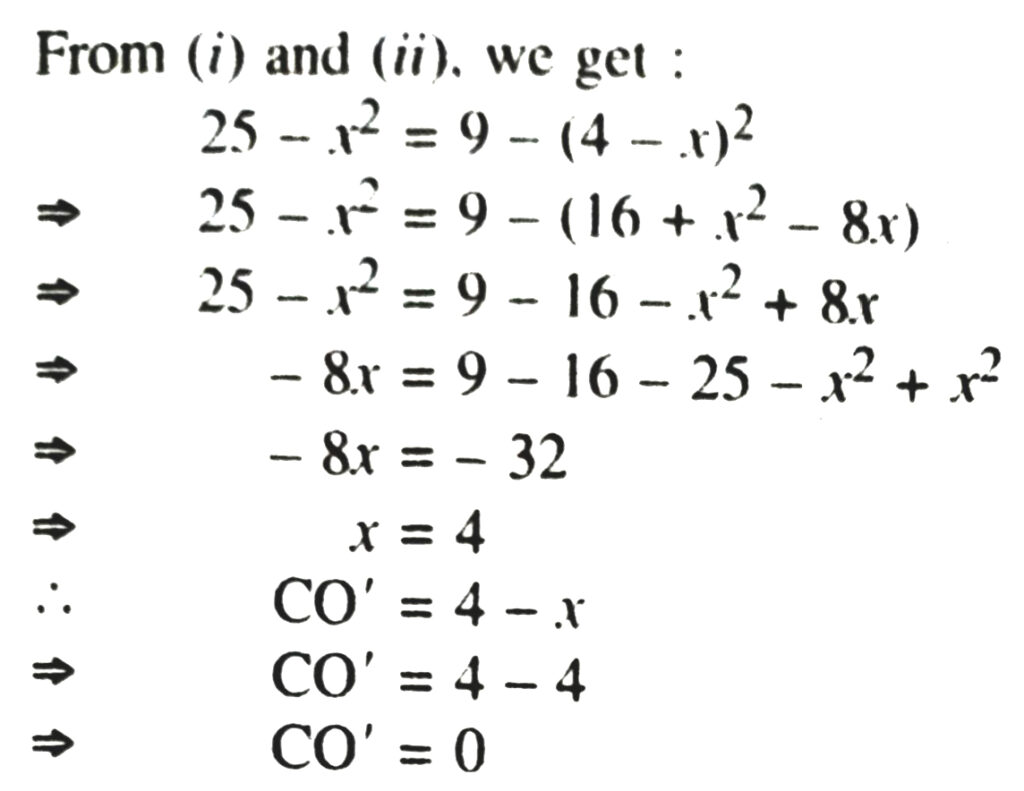
It means that O’coincides with C.
∴ AC = Radius, AO’ = 3 cm.
Length of chord AB = Diameter of circle with centre O’
∴ Length of chord AB = 2 x AO’
= 2 × AC
= 2 × 3
= 6 cm.
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution.— Let AB and CD are two equal chords of a circle of centres O intersecting each other at point E within the circle.


3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
Solution.— AB and CD be two equal chords of a circle with centre O intersecting each other with in
the circle at point E. OE is joined. We have to prove that

4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D prove that AB = CD (See Fig.).
Solution.— Line l intersects two concentric circles with centre O at points A, B, C and D.

5. Three girls Reshma, Salma and Mandip are standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip ?
Solution.— Let position of Reshma, Salma and Mandip is denoted by points A, B and C.
Given that the distance between Reshma and Salma is 6 m and distance between Salma and Mandip is 6 m. It means :


6. A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution.— Let position of three boys Ankur, Syed, Ahmad and David is denoted by points A, B and C.
Three point are at equal distances.
∴ AB = BC = AC = a m (say)
Equal sides of equilateral triangles are as equal chords and perpendicular distances of equal chords of a circle are equidistant from the centre.
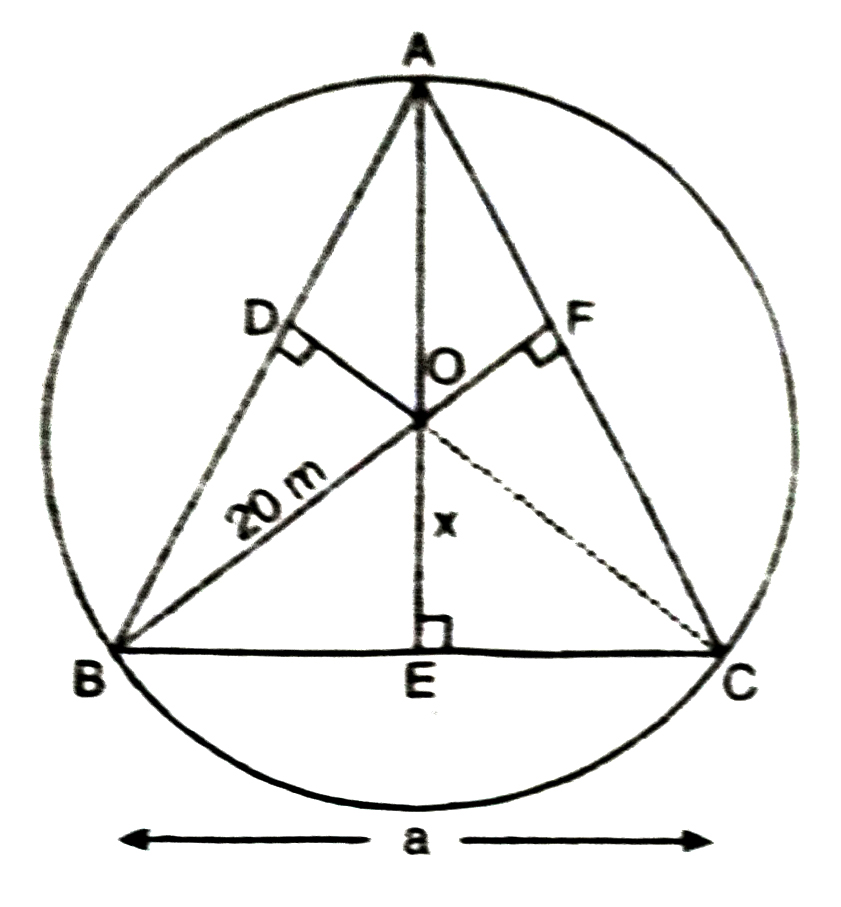


Thus distance between any two boys is 20√3m.
THEOREMS ON ARCS AND THE ANGLES SUBTENDED BY THEM
In this section you will derive some results on angles subtended by arcs of a circle either at centre of the circle or at a point on its circumference.
THEOREM 1. The degree measure of an arc of circle is twice the angles subtended by it at any point of the alternate segment of the circle with respect to the arc.
Given : An arc PQ of a circle C(O, r) with a point R in QP other than P or Q.
To Prove : m PQ = 2 ∠PRQ
Construction : Join RO and produce it to a point M i.e. draw ray ROM. Join PQ.
Proof : Three different cases arise :
(i) PQ is a minor arc (ii) PQ is a semi-circle and (iii) PQ is a major arc.


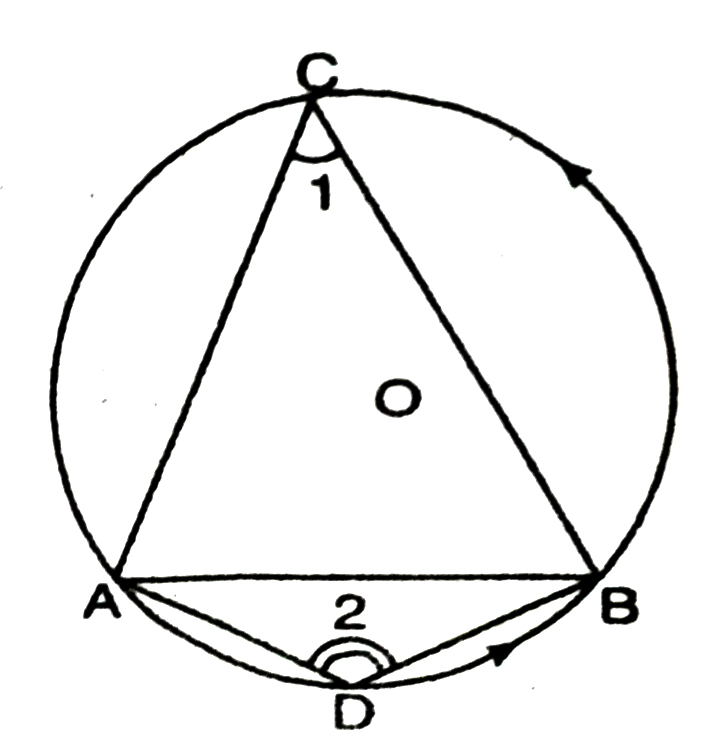
THEOREM 2. Prove that the angles in same segment of a circle are equal.
Given : A circle with centre 0, ∠2 and ∠3 are subtended by the same AMB of the circle at C and D respectively and these two angles are in the same segment.
To prove : ∠2 = ∠3

[Angles in the same segment]
Construction : Join OA and OB.
Steps of Proof : AMB subtends ∠1 at the centre O and ∠2 at the remaining part of the circle.
∴ ∠1 = 2∠2 …(a)
[ ∴ Angle at centre = double the ∠ at any point]
Similarly, we have : ∠1 = 2 ∠3 …(b)
From (a) and (b), we get
∠1 = ∠2∠
∠1 = 2∠3 ⇒ 2∠2 = 2∠3 ⇒ ∠2 = ∠3.
Thus, we have proved that the angles in the same segment of the circle are equal.
THEOREM 3. Prove that angle in a semi-circle is right angle.
Given : A circle with centre O and AOB is its diameter and so it divides the given circle into two congruent semi-circles. C is any point on the semi-circle ACB as shown in the fig.
To Prove : ∠ACB = 90°
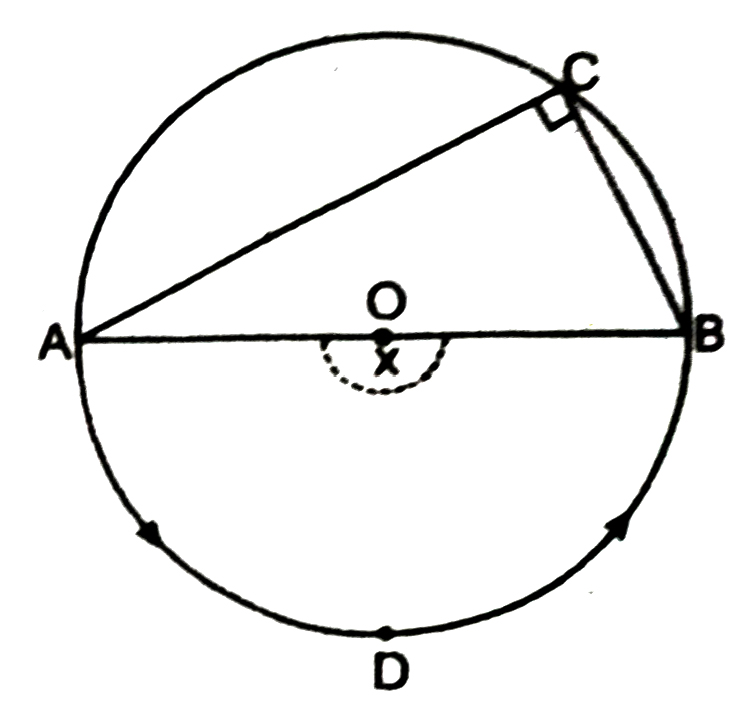
Proof : ADB subtends ∠x at centre O and the same arc subtends ∠ACB at the remaining part of the circle, then by fundamental theorem on circle, we have :
∠x = 2 ∠ABC
[∴ Angle at centre = Twice the angle at any point]
But ∠x is a straight angle and so its measure is 180°.
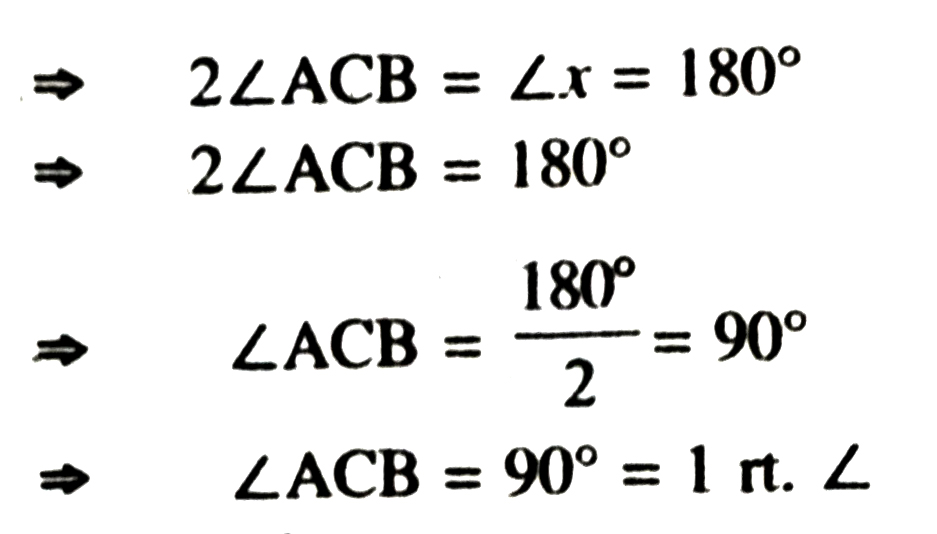
Thus we have proved that the angle in a semi-circle is right angle.
Corollary : Any angle subtended by a minor arc in the alternate segment is acute and any angle subtended by major arc in the alternate segment is obtuse.
Proof : Let AB be a minor arc and C be a point in BA other than A and B.
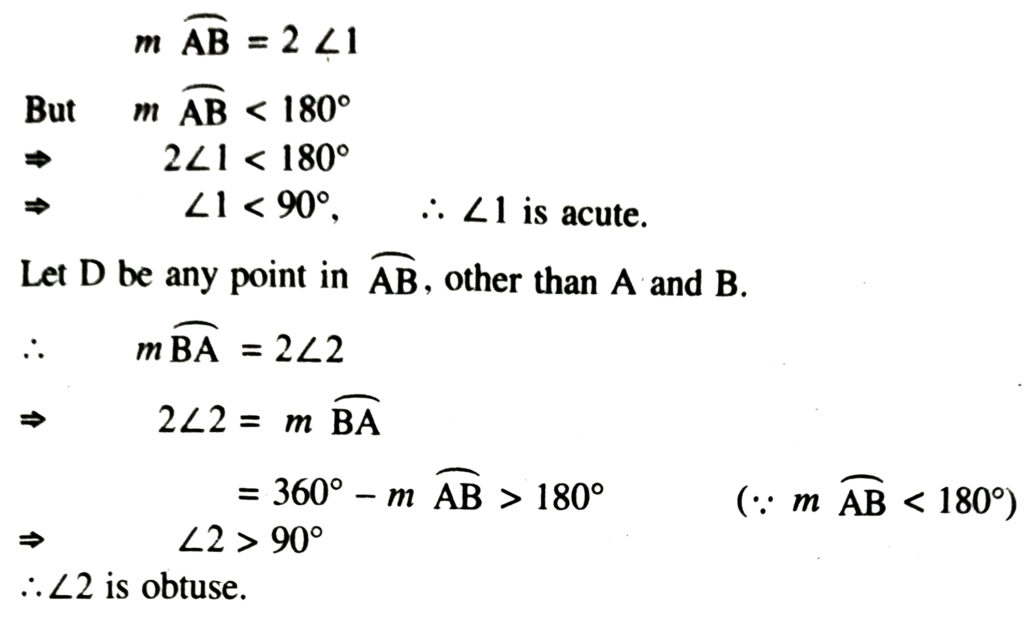
Since all the angles subtended by an arc in the alternate segment are equal, hence, the corollary follows.
THEOREM 4.
(CONVERSE OF THEOREM 3)
The arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semi-circle.
Given : AB is an arc of a circle C(O, r) subtending a right angle at a point C of BA. other than A and B. i.e. 41 = 90°

⇒ m AB = 180º
∴ AB is a semi-circle.
THEOREM 5. If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the segment, the four points are concyclic (i.e. lie on the same circle).
Given : BC is a line segment and A, D are two points lying on the same side of the line containing BC such that :
∠1 = ∠2
To Prove : A, B, C, D are concyclic.
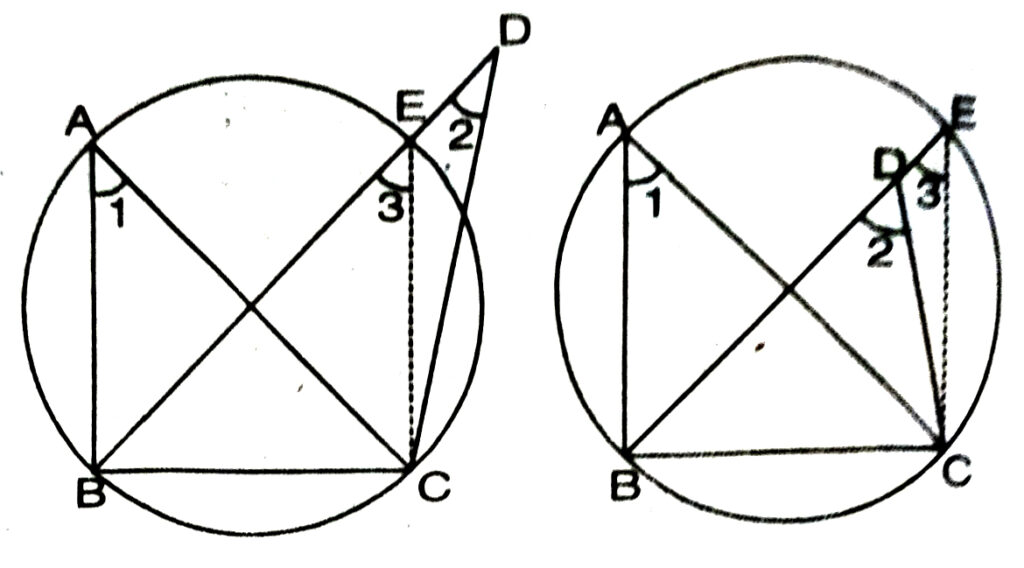
Proof : (By contradiction Method)
If possible, suppose that all the four points A, B, C and D do not lie on the same circle. Draw a circle passing through three non-collinear points A, B and C and which does not pass through D. Let it cut the line segment BD or BD produced in E. Join EC.
∴ ∠1 = ∠3 …(1)
…(Angles in the same segment)
(given)…(2)
But ∠1 = ∠2 From (1) and (2), we get :
∠3 = ∠2
This is impossible, since an exterior angle of a triangle is always greater than either of its interior opposite angle.
∴ Our supposition is wrong.
Hence, the circle passing through A, B and C will pass through D.
∴ The four points A, B, C and D are concyclic.
CYCLIC QUADRILATERAL
Definition. A quadrilateral is called cyclic if all the four of its vertices lie on a circle.
Theorem 1. The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Or
The opposite angles of a cyclic quadrilateral are supplementary.
Given : A cyclic quadrilateral ABCD, the vertices being points on a circle with centre O.
To Prove : ∠B + ∠D = 180°
∠A + ∠C = 180°
Construction : Join O to A and C.
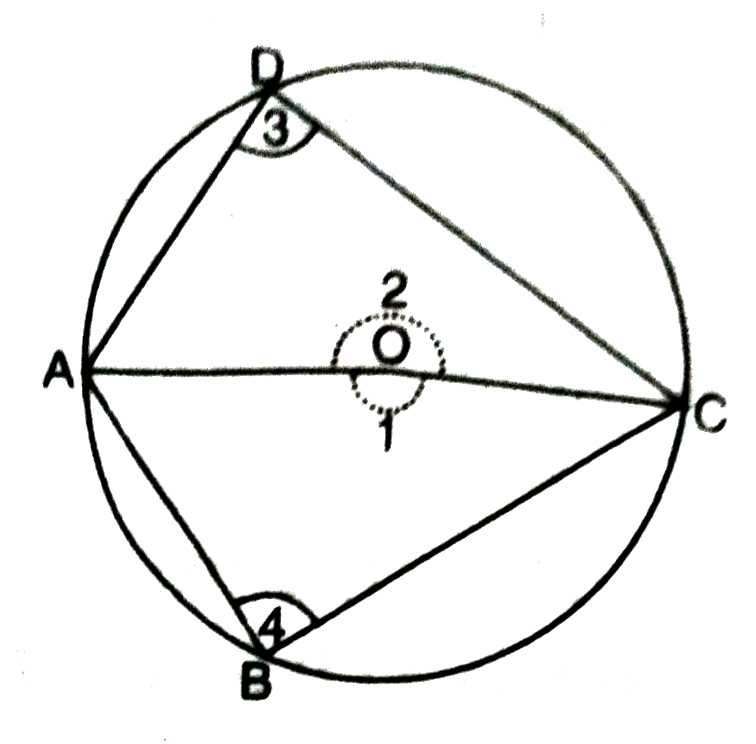
Proof : Since ABC subtending ∠1 at the centre O and ∠3 at any point o la tiet D in the remaining part of the circle.
∴ Angle subtended by an arc at the centre is double the angle at any point of the alternate segment of the circle with respect to the arc.
Therefore, ∠1 = 2 ∠3
Then ∠2 = 2∠4
Adding (i) and (ii), we get :

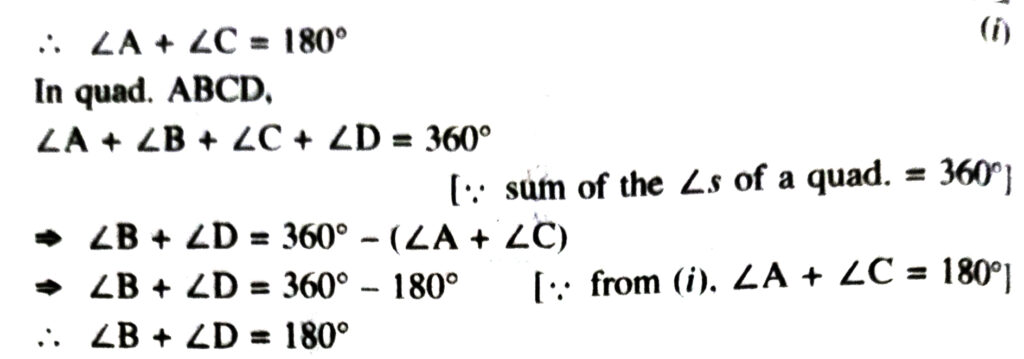
TEXT BOOK EXERCISE – 10.5
1. In Fig., A, B, C are three points on a circle with centre O such that ∠BOC = 30°, ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Solution.— ∠AOC = ∠AOB + ∠BOC
⇒ ∠AOC = 60° + 30°
⇒ ∠AOC = 90°

Now
∠AOC = 2∠ADC
[∴ angle subtended by an arc, at the centre of the circle is double the angle subtended by the same arc at any point in the remaining part of the circle]
or ∠ADC = 1/2 ∠AOC
⇒ ∠ADC = 1/2 × 90º
⇒ ∠ADC = 45°.
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.

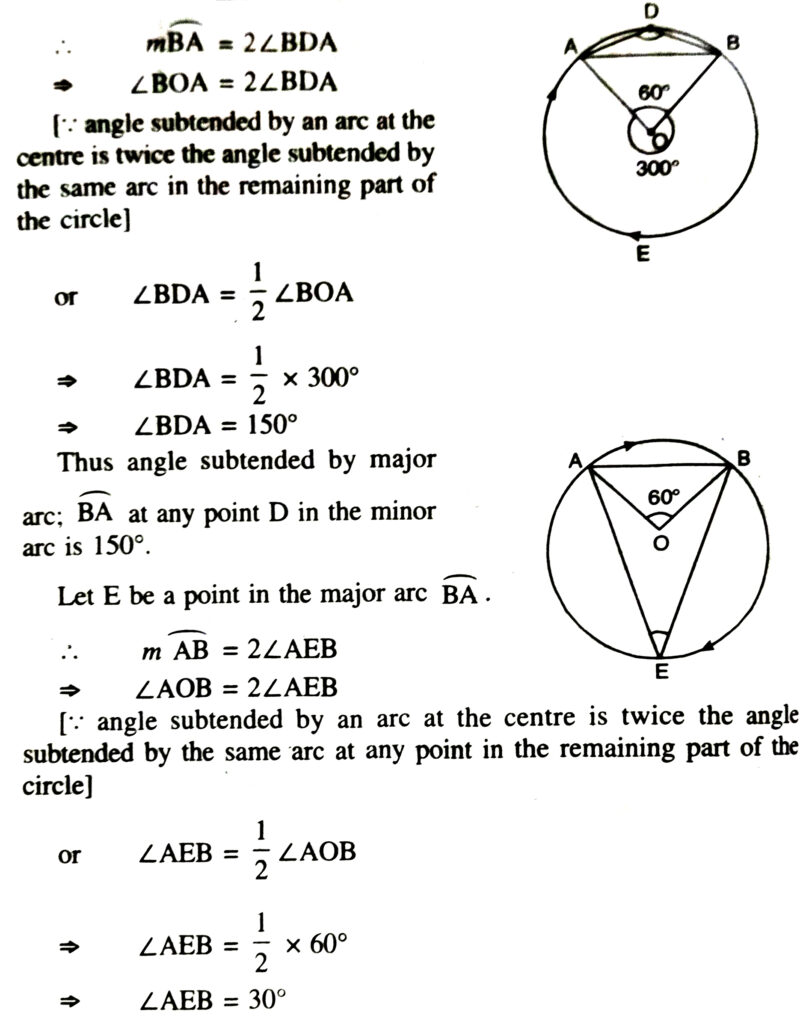
Thus angle subtended by minor arc; AB at any point E in the major arc is 30°.
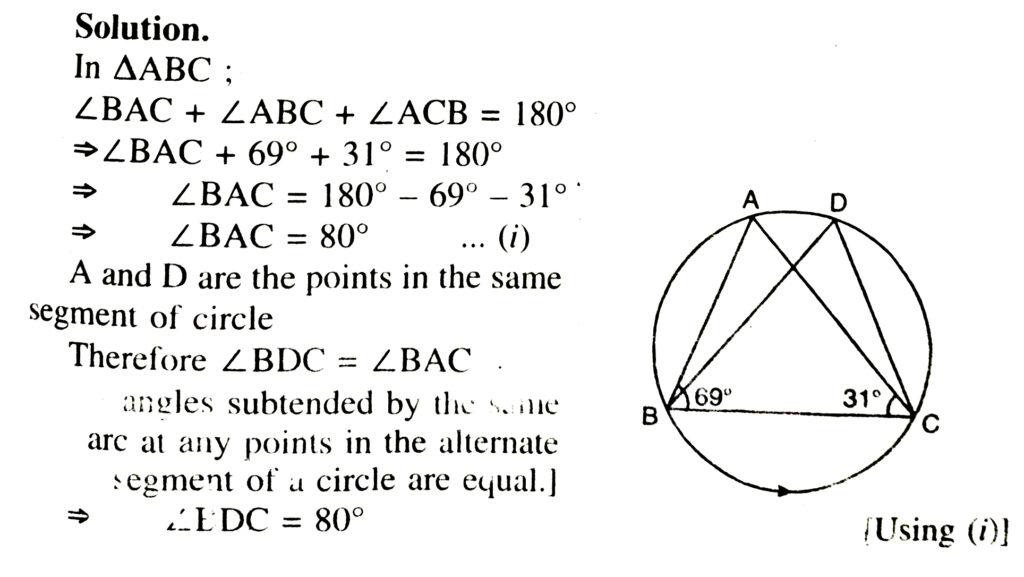
3. In fig., ∠PQR = 100°, where P, Q, R are points on a circle with centre O. Find ∠OPR.
Solution.— In fig. ; Q is a point in the minor arc PQR
∴ mRP = ∠PQR
⇒ ∠ROP = 2∠PQR
[∴ angle subtended by an arc at the centre is twice the angle subtended by the same arc at any point in the remaining part of the circle]

4. In fig., ∠ABC = 69°, ∠ACB = 31°, find ∠BDC. Solution.
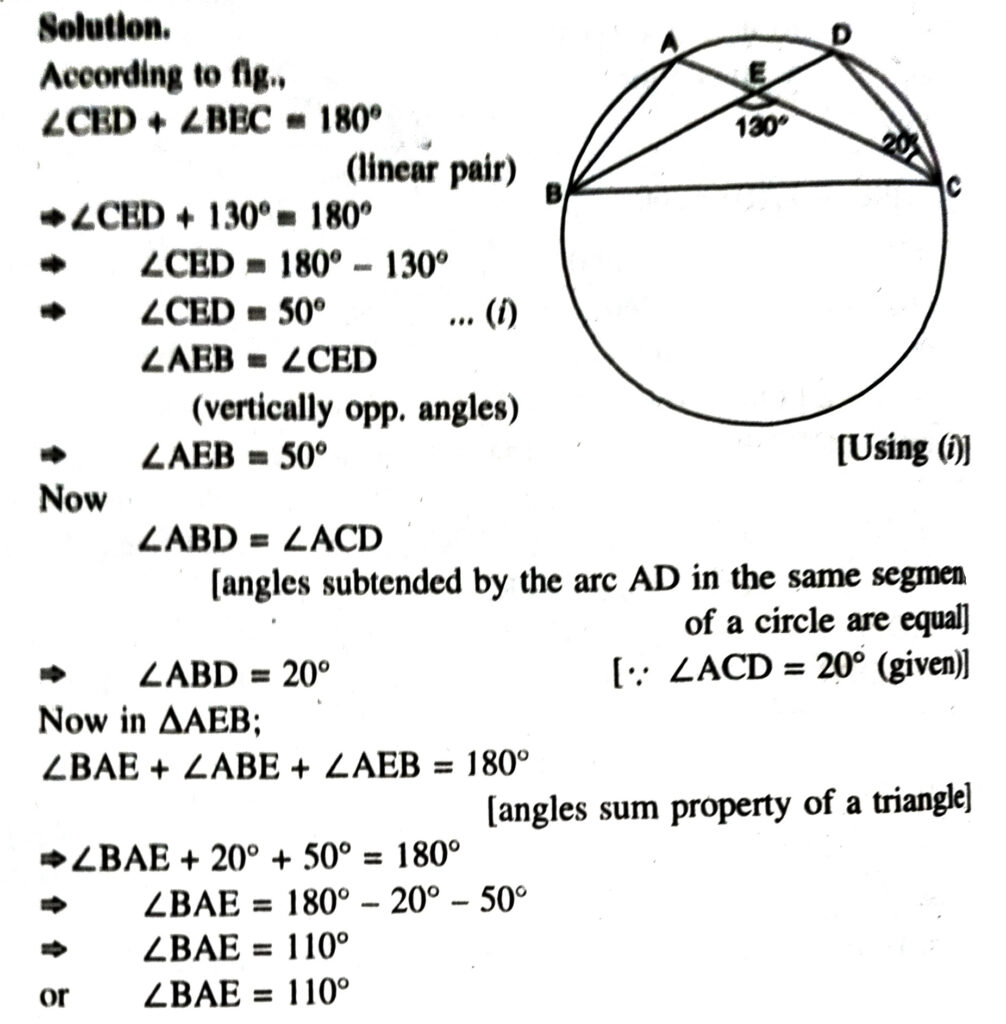
5. In fig., A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
6. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Solution.— We have ABC and ADC two right triangles rt. angles at B and D respectively.
∴ ∠ZABC = ∠ADC (each 90°)
If we draw a circle with AC (the common hypotenuse) as diameter, this circle will definitely passes through points B and D.
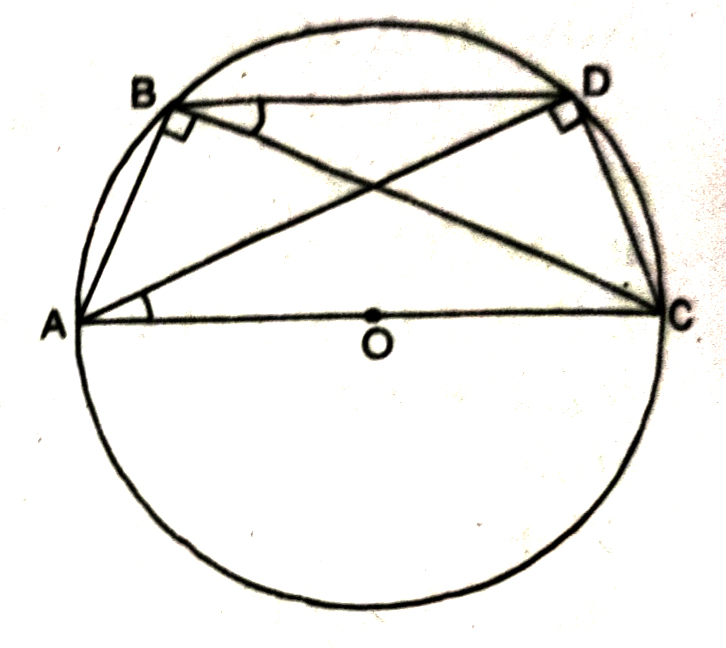
[Because B and D are the points in the alternate segment of an arc AC.]
Now we have CD subtending ∠CBD and ∠CAD in the same segment.
∴ ∠CAD = ∠CBD (Proved)
7. Prove that a cyclic parallelogram is a rectangle.
Solution.— Let ABCD be a cyclic parallelogram. To prove that it is a rectangle, it is sufficient to show that one of the angles of parallelogram ABCD is a right angle.
Now ABCD is a parallelogram
⇒ ∠B = ∠D …(i)
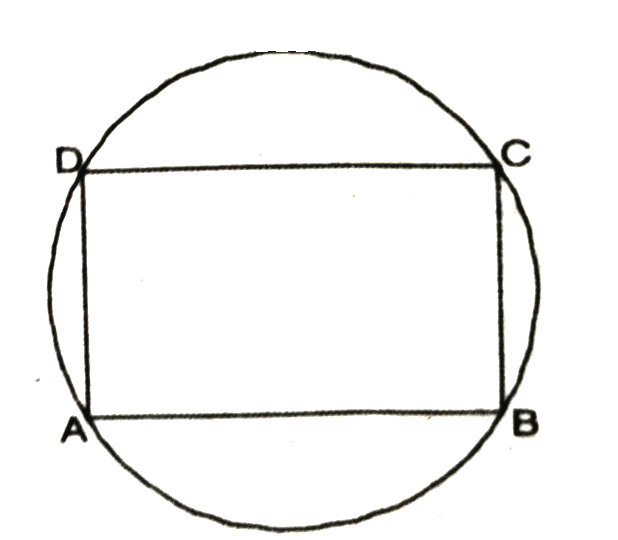
[∴ Opposite angles of a llgm are equal]
Also, ABCD is a cyclic quadrilateral.
⇒ ∠B + ∠D = 180°
From (i) and (ii), we get :
∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°
Thus ∠B = ∠D = 90°
Hence ABCD is a rectangle.
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here