JKBOSE 9th Class Mathematics Solutions Chapter 6 Lines and Angles
JKBOSE 9th Class Mathematics Solutions Chapter 6 Lines and Angles
JKBOSE 9th Class Mathematics Solutions Chapter 6 Lines and Angles
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Lines and Angles Textbook Questions and Answers
INTRODUCTION
The word ‘geometry’ comes from the Greek ‘geo’ meaning the ‘earth’ and ‘metrein’ meaning ‘to measure’. Geometry appears to have originated from the need for measuring land. This branch was studied in various forms in every ancient civilization, be it in Egypt, Babylonia, China, India, Greece, the Incas, etc. The people of these civilizations faced several practical problems which required the development of geometry in various ways.
It is believed that the knowledge of geometry passed on from Egyptians to Greeks, who gave it a systematic treatment. A Greek mathematician, Thales (640 B.C. – 546 B.C.) is credited with giving the first known proof. This proof was of the statement that a circle is bisected by its diameter.

One of Thale’s most famous pupils Thales (640 B.C. – 546 B.C.) was Pythagoras (572 B.C.), whom you have heard about. Pythagoras and his group discovered many geometric properties and developed the theory of geometry to a great extent. This process continued till 300 B.C. At that time Euclid, a teacher of mathematics at Alexandria, in Egypt, collected all the known work and arranged it in his Euclid (325 B.C. – 265 B.C.) famous ‘Elements’. He divided ‘Elements’ into thirteen chapters, each called a book. These books influenced the whole world’s understanding of geometry for generations to come. In this chapter, we shall discuss Euclid’s appraoch to geometry and shall try to link it with the present day geometry.

EUCLID’S ELEMENTS ELEMENTS
‘Euclid’s elements’ are generally regarded as forming the basis of geometry, which is in fact now known as ‘Euclidean geometry’. The whole subject is based on establishing a small set of assumptions (obvious universal truth), and building a series of theorems and proofs based on these. These assumptions are called ‘definitions’, ‘postulates’ and ‘common notions’.
The postulates are the assumptions that were specific to the geometry. Common notions often called axioms on the other hand are assumptions used throughout mathematics and not specifically linked to geometry.
EUCLID’S DEFINITIONS
Euclid begins his exposition by listing 23 definitions in the book 1 of the ‘Elements’. These are given as follows :
1. A point is that which has no part.
2. A line is breadthless length.
3. The extremities of a line are points.
4. A straight line is a line which lies evenly with the points on itself.
5. A surface is that which has length and breadth only.
6. The extremities of a surface are lines.
7. A plane surface is a surface which lies evenly with the straight lines on itself.
8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
9. And when the lines containing the angle are straight, the angle is called rectilineal.
10. When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
11. An obtuse angle is an angle greater than a right angle.
12. An acute angle is an angle less than a right angle.
13. A boundary is that which is an extremity of anything.
14. A figure is that which is contained by any boundary or boundaries.
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another.
16. And the point is called the centre of the circle.
17. A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
19. Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
20. Of trilateral figures, an equilateral triangle is what which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor rightangled. And let quadrilaterals other than these be called trapezia.
23. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
Euclid’s axioms (or common notions)
Some of the Euclid’s axioms not in the order are given below :
1. Things which are equal to the same thing are equal to one another.
2. If equals are added to equals, the wholes are equal.
3. If equals are subtracted from equals, the remainders are equal.
4. Things which coincide with one another are equal to one another.
5. The whole is greater than the part.
6. Things which are double of the same things are equal to one another.
7. Things which are halves of the same things are equal to one another.
These common notions refer to magnitudes of some kind. The first common notion could be applied to plane figures. For example, if an area of a triangle equals the area of a rectangle and the area of a rectangle equals that of a square, then the area of a triangle also equals the area of a square. Magnitudes of the same kind can be compared and added, but magnitudes of different kinds cannot be compared. For example, a line cannot be added to a rectangle, nor can an angle be compared to a pentagon.
Common notion (4) given above seems to say that if two things are identical (that is, they are the same one), then they are equal. In other words, anything equals itself. It is the justification of a principle of superposition. Common notion (5) gives us the definiton of ‘greater than’. For example, if one magnitude B is a part of another A, then A can be expressed as the sum of B and C for some third magnitude C,5 the remainder. Symbolically, A > B means that there is some C such that A = B + C.
EUCLID’S POSTULATES
1. A straight line may be drawn from any one point to any other point.
Note that this postulate assures atleast one straight line passing through two distinct points but it does not assure that there cannot be more than such line. However, in his work, Euclid has frequenty assumed, without mentioning, that these is a unique line joining two distinct points. We state this result in the form of an axiom as follows d
Axiom 1.1. Given two distinct points, there is a unique line that passes through them (see Fig.)
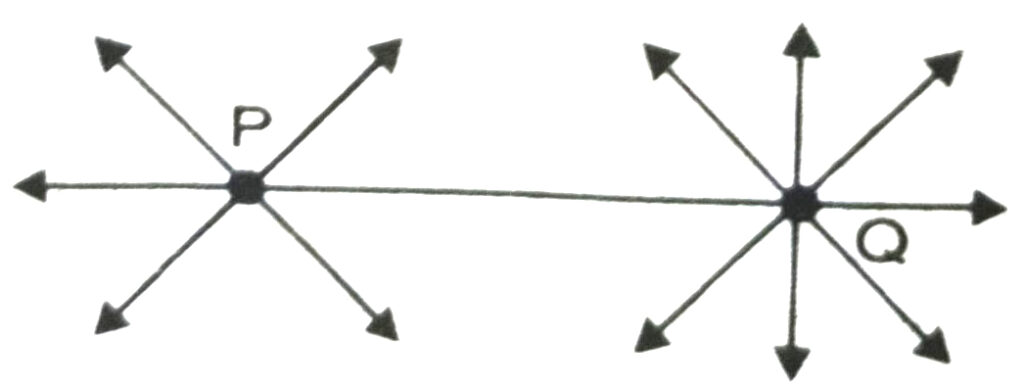
How many lines passing through P also pass through Q ? Only one, that is, the line PQ. How many lines passing through Q also pass through P? Only one, that is, the line PQ. Thus, the statement above is self-evident.
2. A terminated line can be produced indefinitely [see Fig.].

3. A circle can be drawn with any centre and any radius.
4. All right angles are equal to one another.
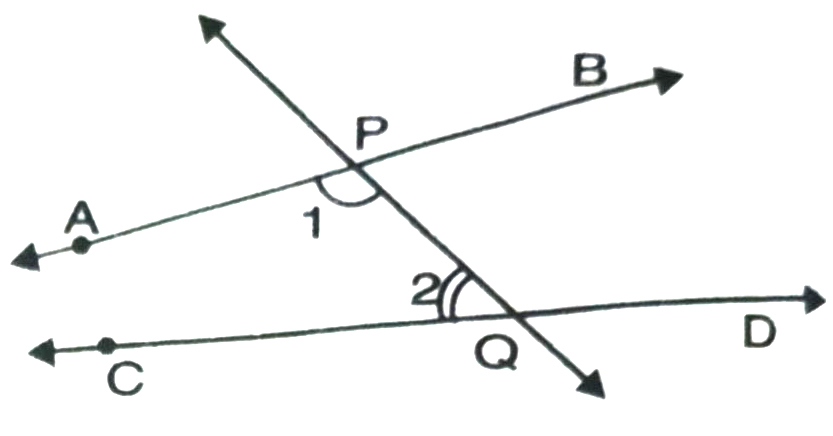
5. If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced idenfinitely, meet on that side on which the angles are less than two right angles (see Fig. ). The line PQ falls on lines AB and CD.
Euclid’s Propositions/theorems
Using these postulates and axioms, Euclid started proving other results. Then using these results, he proved some more results using deductive logic (see Appendix 1). These proved statements are called as the propositions/theorems (see Appendix 1). Euclid deduced 465 propositions in a logical chain using his axioms, postulates and definitions. In the next chapters of the unit on geometry, you may use these axioms to prove more theorems.
Now, let us see in the following examples how the axioms and postulates are used for proving some of the results :
Euclid’s Proposition
Proposition.
To bisect a given rectilineal angle.
Let the angle BAC be given rectilineal angle. Thus it is required to bisect it.
We shall use Euclid’s axiom (4) to prove this statement.
Let a point D be taken at random on AB; let AE be cut off from AC equal to AD. Let DE be joined and on DE. Let the equilateral triangle DEF be constructed. Let AF be joined.
We say that angle BAC has been bisected by the straight line AF. For, since AD is equal to AE and AF is common, the two sides DA, AF are equal to the two sides EA, AF respectively. And the base DF is equal to the base EF, therefore the angle DAF is equal to the angle EAF.
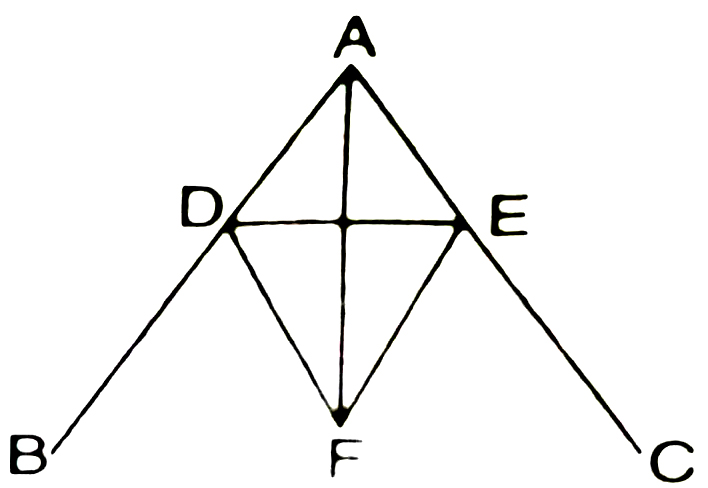
Thus the given rectilineal angle BAC has been bisected by the straight line AF.
Theorem 1. Two distinct lines cannot have more than one point in common.
Proof. Here, we are given two lines l and m. We need to prove that lines l and m have only one point P in common.
For some time, let us consider that the two lines intersect in two distinct points say P and Q.
So, you have two lines passing through two distinct points P and Q. But this assumption clashes with the Axiom 1.1 that only one line can pass through two distinct points. So, the assumption that two lines can pass through two distinct points is wrong.
Equivalent Versions of Euclid’s Fifth Postulate
Euclid’s fifth postulate is very significant in mathematics and its history. Refer it again from previous Section. We see that by implication, no intersection will take place when the sum of the measures of the interior angles on the same side of the falling line is exactly 180º. There are several equivalent versions of this postulate. One of them is ‘Playfair’s Axiom’, (given by a Scottish mathematician John Playfair in 1729), as given below :
‘For every line l and for every point P not lying on l, there exists a unique line m passing through P and is parallel to l‘ [see Fig. ].
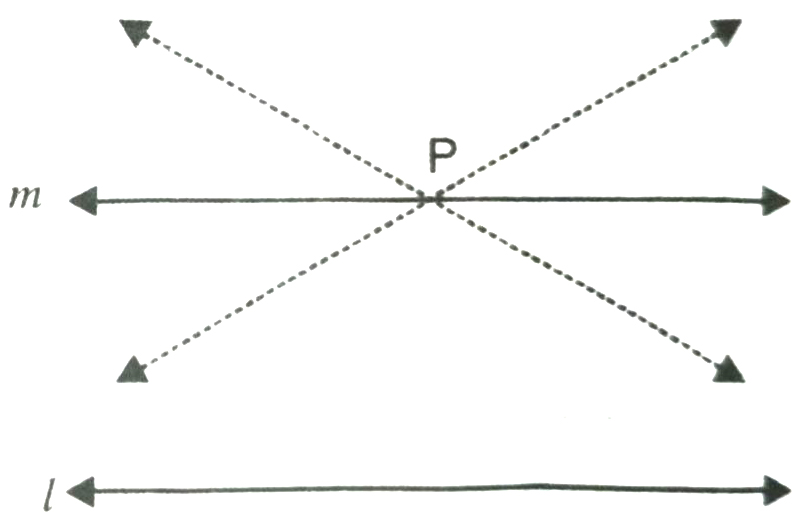
Clearly, of all the lines passing through the point P, only line m is parallel to line l.
Euclid did not require his fifth postulate to prove his first 28 theorems. Many mathematicians including him were convinced that the fifth postulate is actually a theorem that can be proved using just the first four postulates and other axioms. However, all attempts to prove the fifth postulate as a theorem have failed. But these efforts have led to a great achievement the creation of several other geometries. These geometries are quite different from Euclidean geomery. They are called non-Euclidean geometries. The creation is considered a landmark in the history of thought because till then everyone had believed that Euclid’s was the only geometry and the world itself was Euclidean.
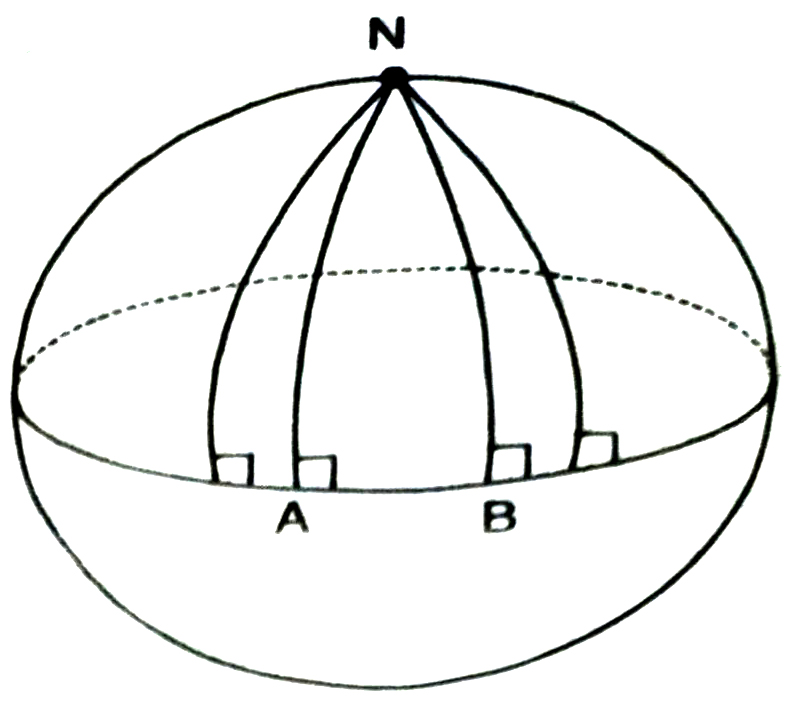
Now the geometry of the universe we live in has been demonstrated to be a non-Euclidean geometry. In fact, it is called spherical geometry. In spherical geometry, lines are not straight. They are parts of great circles (i.e. circles obtained by intersection of planes with the sphere).
In Fig., the lines AN and BN (which are parts of great circles of the sphere) are perpendicular to the same line AB. But they are meeting each other though the sum of the angles on the same side of line AB is not less than two right angles (infact, it is 90° +90° = 180°). Also, note that the sum of the angles of the triangle NAB is greater than 180°, as ∠A + ∠B = 180°. Thus Euclidean geometry is valid only for the figures in the plane. On the curved surfaces, it fails. Now, let us do an example.
Example. Consider the following statement: There exists a pair of straight lines that are everywhere equidistant from one another. Do you think that this statement is (or is not) a direct consequence of Euclid’s fifth postulate ? Explain.
Solution. See Fig. (i). Since ∠1 + ∠2 is less than 180°, according to Postulate (5) the lines I and m will meet on right side of line n, say point R.
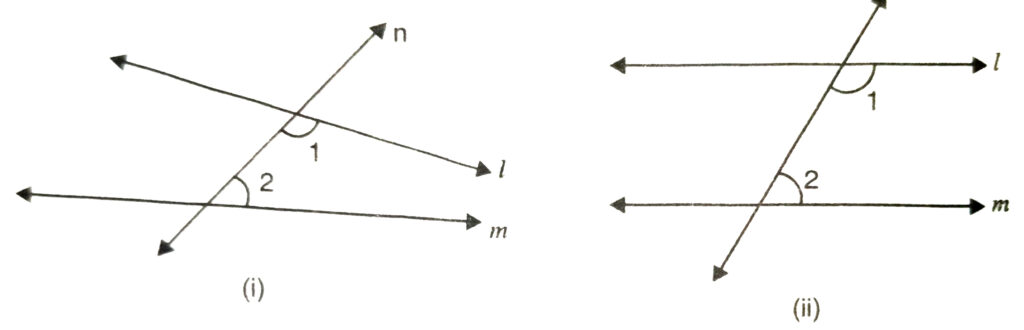
But if ∠1 + ∠2 = 180°, then according to Playfair’s axiom the lines l and m will not meet each other [see Fig. (ii)]. In Fig. (i), you can see that the distance between the two lines goes on decreasing as you move on right side and finally becomes zero.
Fundamental Axioms and Theorems
Incidence Axiom : 1. A line contains infinitely many points.
Incidence Axiom : 2. Through given points, there passes infinitely many lines.
Incidence Axiom : 3. Give two distinct points A and, B, there is one line that contains both the points.
Definition : Three or more than three points are said to be collinear if there is a line which contains them.
Definition : Three or more than three lines are said to be concurrent if there is a point which lies on all of them.
Theorem 1. Two distinct lines cannot have more than one point in common.
Axiom : 4. If l is a line and p is a point on l there in one and only one line which passes through p and is parallel to l.

Theorem 2. Two lines which are both parallel to the same line are parallel to each other.
Axiom : 5 (Linear pair Axiom) If a ray stands on a line, then the sum of the two adjacent angles so formed is 180°. Conversely if the sum of two adjacent angles is 180°, then the non-common arms of the angles are two opposite rays.
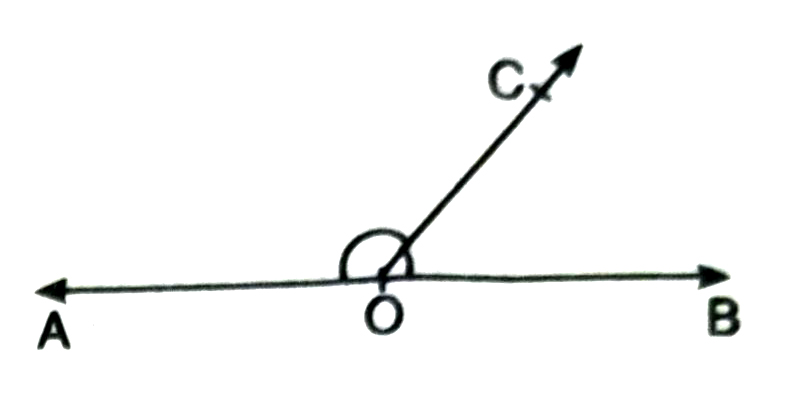
Remarks : You may recall the two angles are said to be supplementary if there sum is 180°. Using this definition, the statement of the linear pair Axiom may also be put as—
Two adjacent angles are a linear pair of angles if and only if they are supplementary.
Theorem 3. If two lines intersect, then the vertically opposite angles are equal.
Given : Lines AB and CD intersect at O (see Fig.)
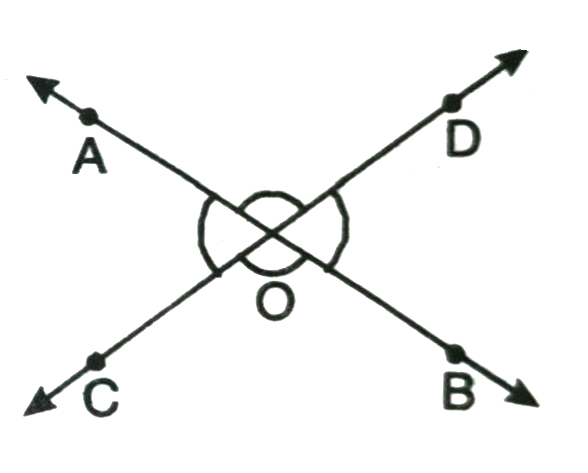
To prove : (1) ∠AOC = ∠DOB,
(2) ∠BOC = ∠DOA
Proof : Ray OD stand on the line AB
∴ ∠AOD + ∠DOB = 180° (linear pair axiom)…(i)
∴ Ray OA stands on line CD
∠AOD + ∠AOC = 80° (linear pair axiom)…(ii)
From (i) & (ii), we have
∠AOD + ∠DOB = ∠AOD + ∠AOC
∴ ∠AOC = ∠DOB
Similarly ∠BOC = ∠DOA.
Axiom : 6. Two angles whose sum is 90° are called complementary angles.
a + b = 90°
a and b are complementary angles.
TEXT BOOK EXERCISE – 6.1
1. In Fig., lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

2. In Fig., lines XY and MN intersect at O. If ∠POY = 90º and a : b = 2 : 3, find c.

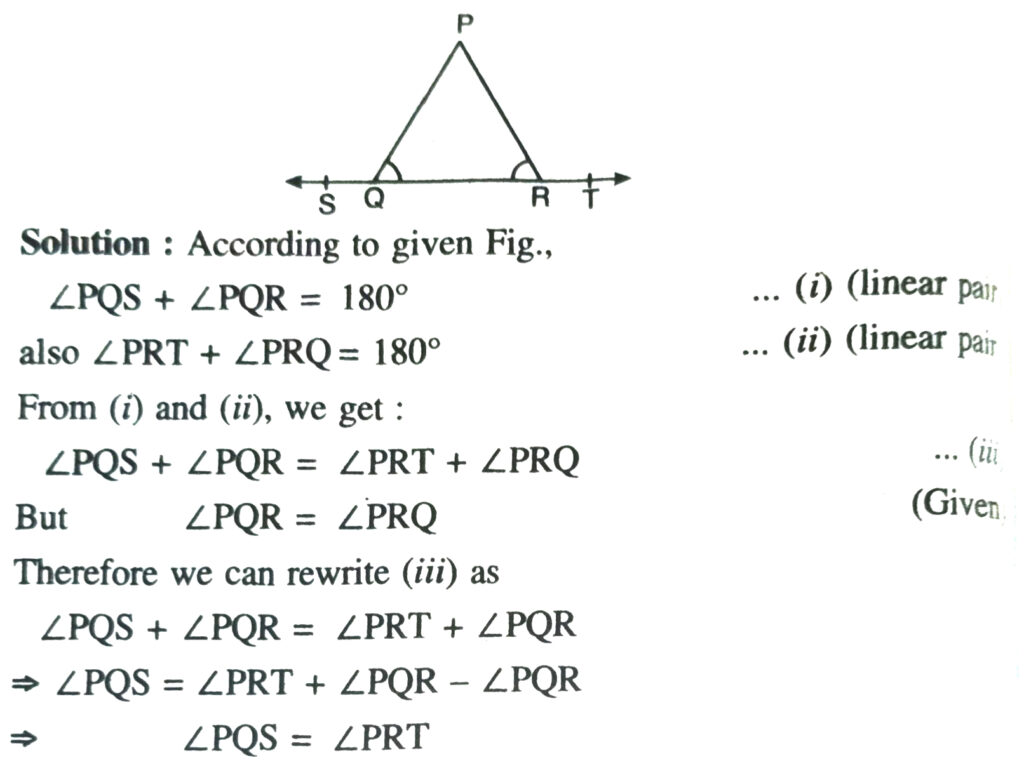
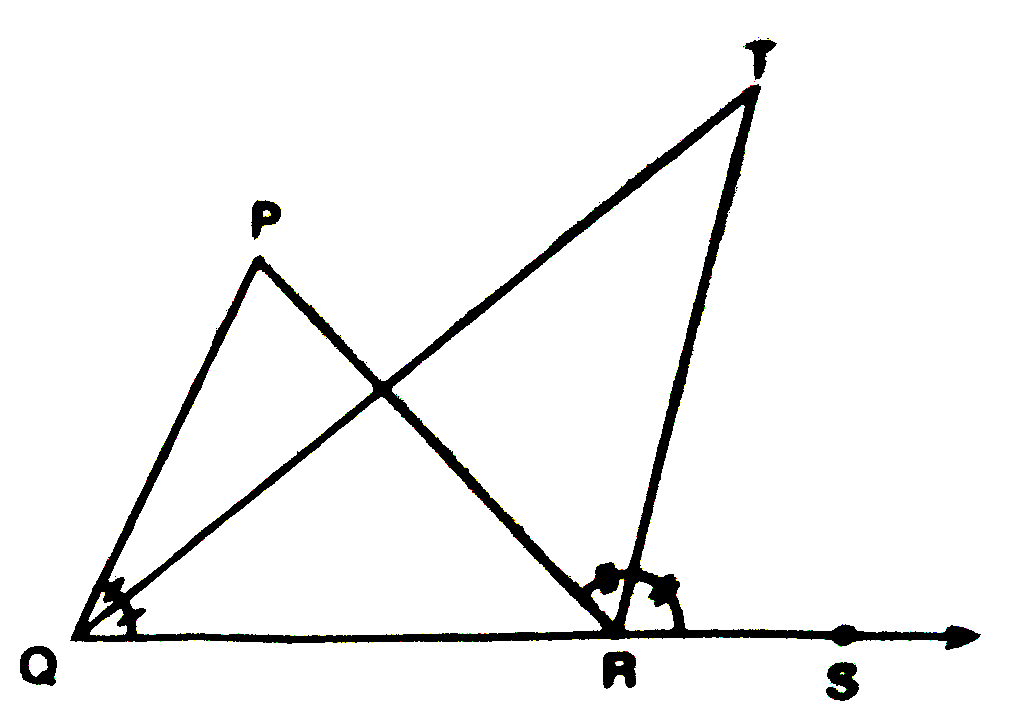
3. In Fig., ∠PRQ = ∠PRQ, then prove that ∠PQS = ∠PRT.
4. In Fig., If x + y = w + z, then prove that AOB is a line.
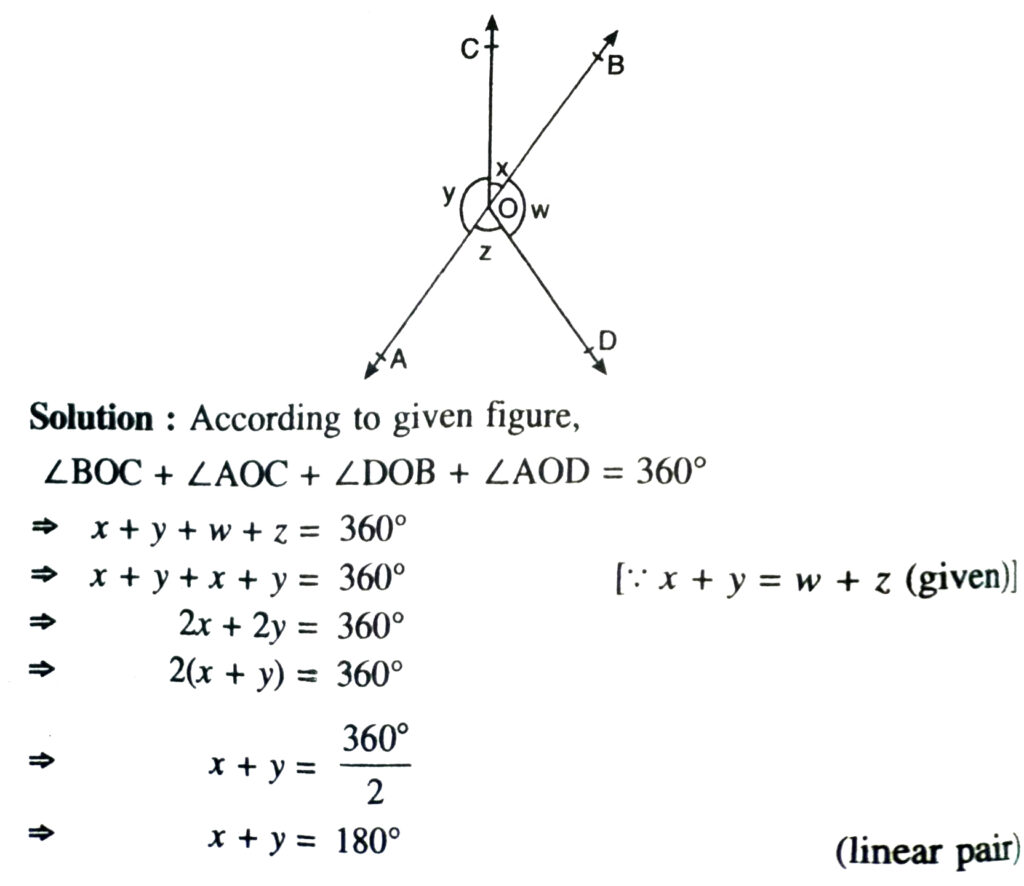
or ∠BOC + ∠AOC = 180º
It Shows that OC is the common arm of angles; ∠AOC and ∠BOC forming a linear pair.
Hence AOB is a line.
5. In Fig., POQ is a line. Ray OR is Perpendicular to line PQ. OS is another ray lying between rays OP and OR.
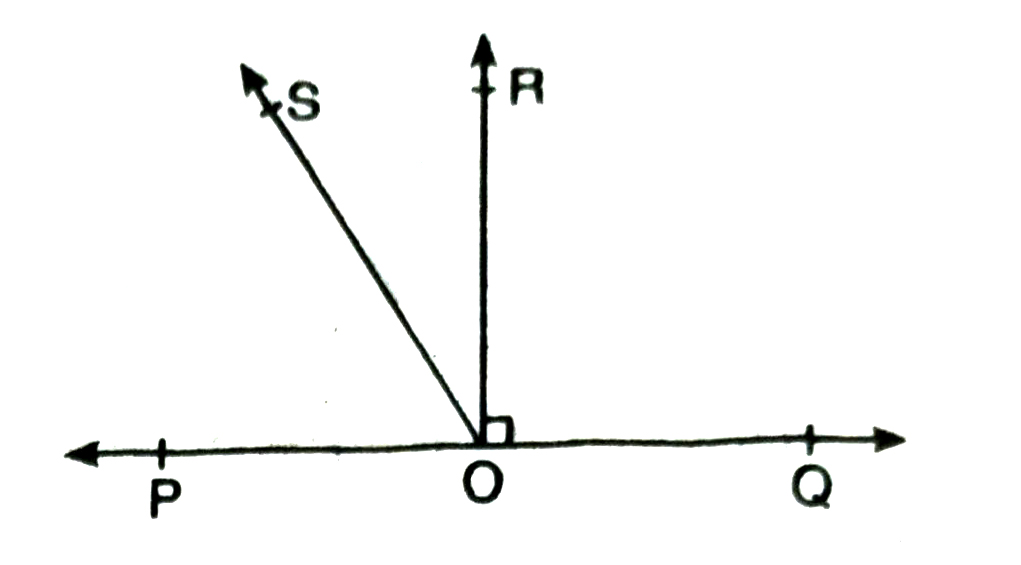
∠ROS = 1/2 (∠QOS – ∠POS

TEXT BOOK EXERCISE – 6.2
1. In fig, find the value of x and y and then show that AB ΙΙ CD.
Solution.— Let transversal l intersects AB and CD at P and Q respectively.
According to given fig,
50° + × = 180° (linear pair)
⇒ x = 180° – 50°
⇒ x = 130° …(i)
y = 130°
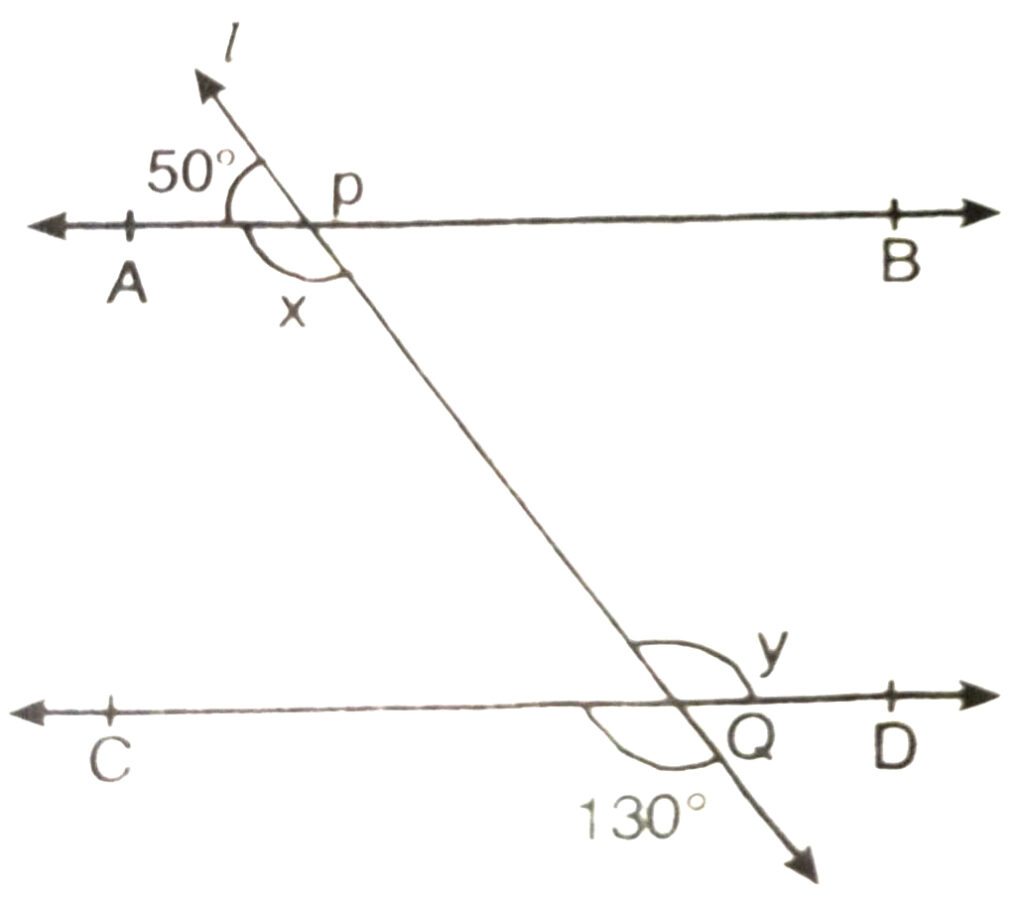
(vertically opposite angles) …(ii)
From (i) and (ii), we observe that :
x = y
It shows that interior, alternate interior angles are equal. As we know that if a transversal (say l) intersects two lines in such a way that a pair of alternate interior angles are equal, then the two lines are parallel.
Therefore, AB ΙΙ CD.
2. In fig., if AB || CD, CD || EF and y: z= 3:7, find x.
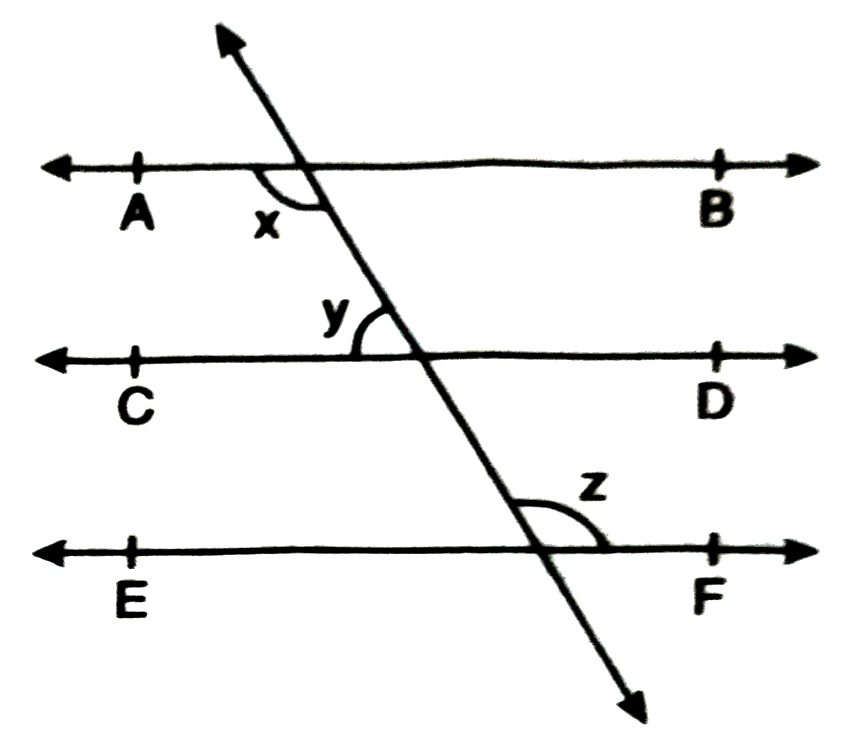

⇒ z = 7 × 18º
⇒ z = 126º
From (ii), we have x = z
∴ x = 126º
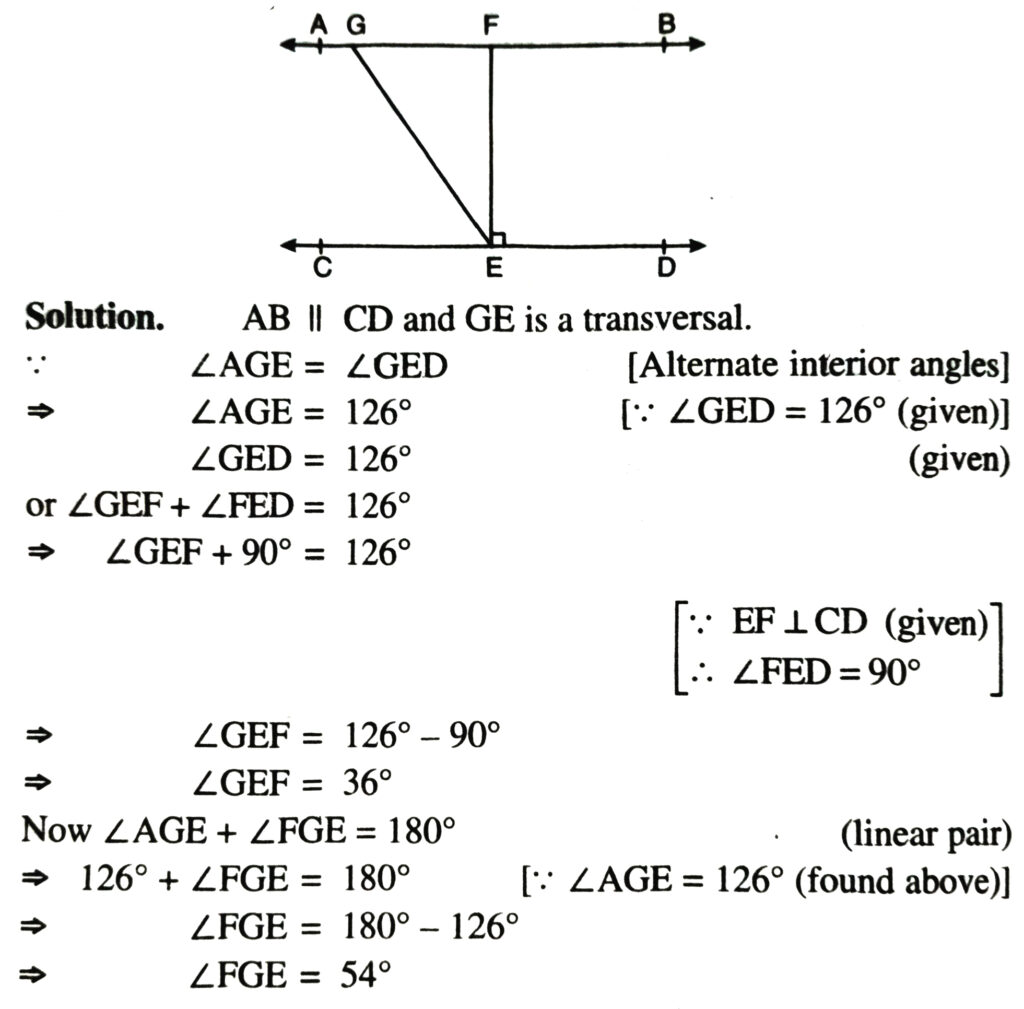
3. In fig., if AB ΙΙ CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
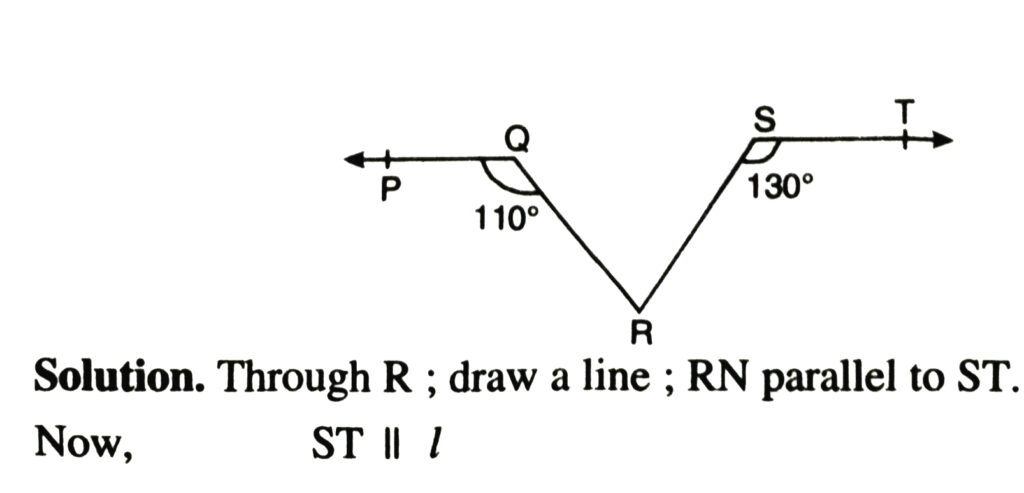
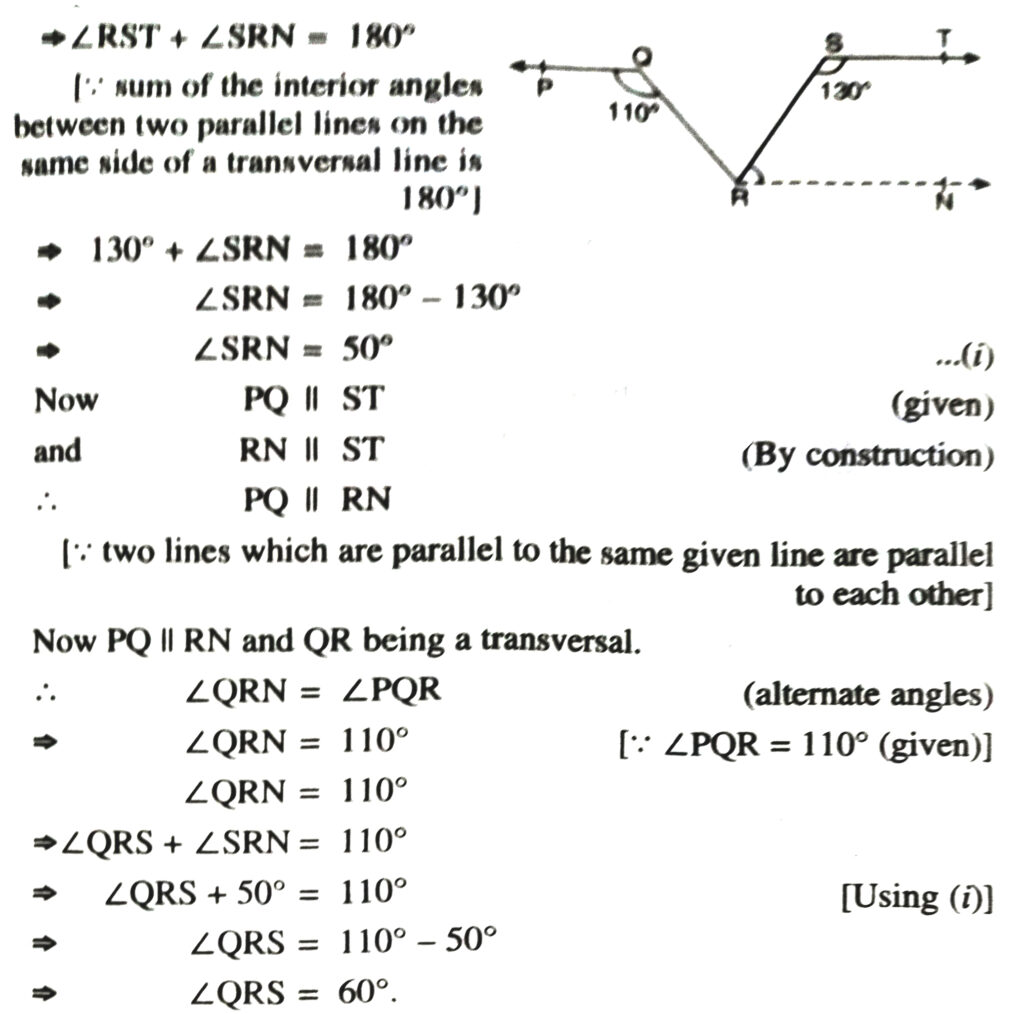
4. In fig., if PQ ΙΙ ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
5. In fig., if AB ΙΙ CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
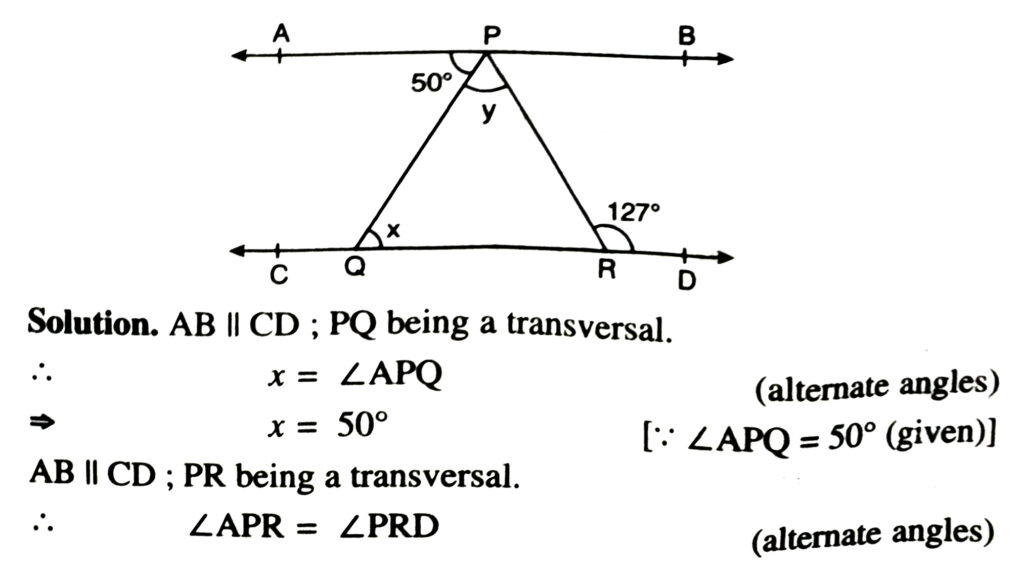
⇒ ∠APQ + ∠QPR = ∠PRD
⇒ 50º + y = 127º
⇒ y = 127º – 50º
⇒ 77º.
6. In fig., PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray move along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ΙΙ CD.
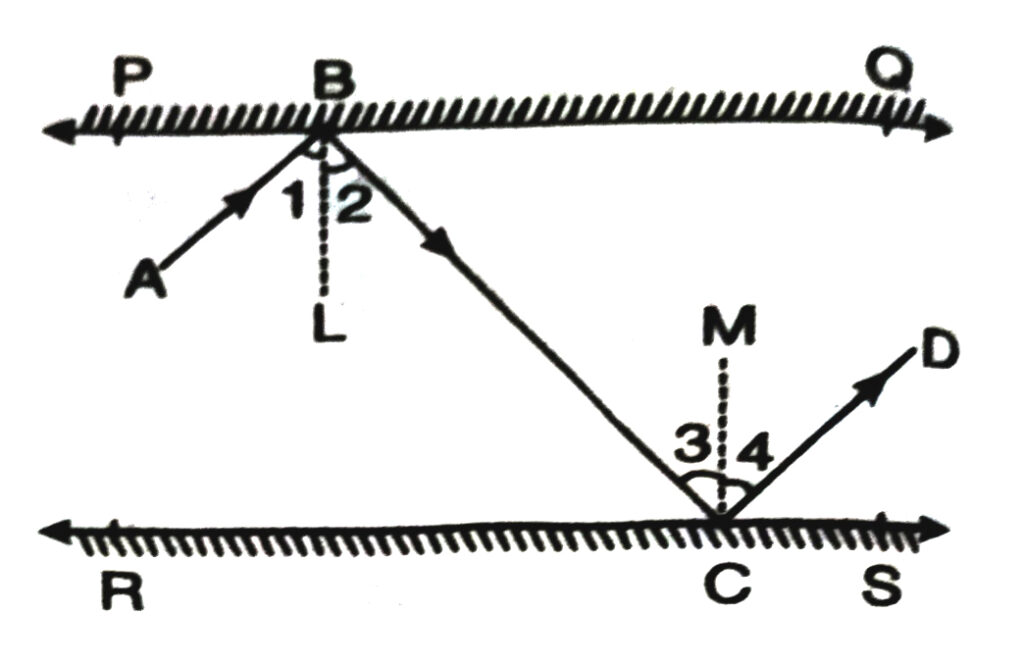
Solution.— According to the given figure; PQ and RS are two plane mirrors parallel to each other. AB is an incident ray strikes the mirror PQ at B. CD is the ray reflected from the mirror RS.
We have to prove that
AB ΙΙ CD
Proof : As we know that
angle of incidence = angle of reflection
∴ ∠1 = ∠2 and ∠3 = ∠4 …(i)
∠1 is the angle between incident ray AB and normal BL
∴ ∠1 is an incident angle, ∠2 is the angle between the reflected ray BC and normal BL. Therefore, 22 is a reflected angle. Similarly ∠3 and ∠4 are the angles of incidence and reflection respectively.
∴ PQ ΙΙ RS and BL ⊥ PQ
and CM ⊥ RS implies that :
BL ΙΙ CM
Now parallel lines BL and CM are cut by a transversal BC.
∴ ∠2 = ∠3 (alternate angles)…(ii)
Now, ∠ABC = ∠1 + ∠2
⇒ ∠ABC = ∠2 + ∠2 [∴ ∠1 = ∠2]
⇒ ∠ABC = 2∠2
and ∠BCD = ∠3 +∠4
⇒ ∠BCD = ∠3 + ∠3 [∴ ∠3 = ∠4]
⇒ ∠BCD = 2∠3
But from (ii), we have :
∠2 = ∠3
⇒ 2∠2 = 2∠3
⇒ ∠ABC = ∠BCD
These are alternate angles. BC being a transversal.
Therefore, AB ΙΙ CD.
TRIANGLES AND ITS ANGLES
Theorem 5. Sum of three angles of triangle is 180°.
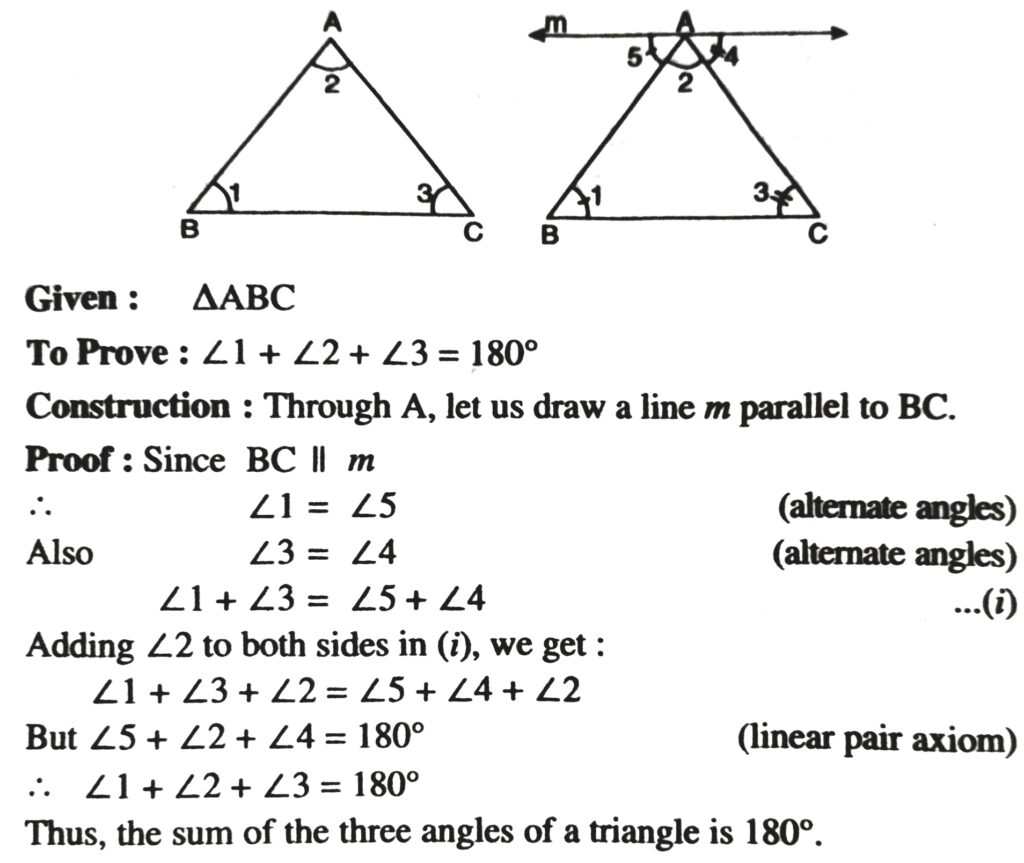
Theorem 6. If a side of a triangle is produced, the exterior angles so formed is equal to the sum of the two interior opposite angles.
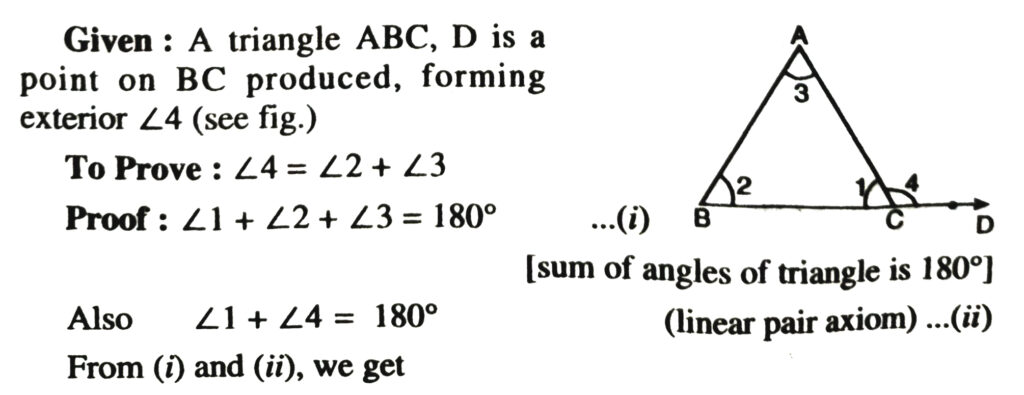
∠1 + ∠2 + ∠3 = ∠4 + ∠1
∴ ∠4 = ∠2 + ∠3.
Corollary : An exterior angle of a triangle is greater than either of the interior opposite angles.
This sometimes also referred to as Exterior Angle Theorem.
TEXT BOOK EXERCISE – 6.3
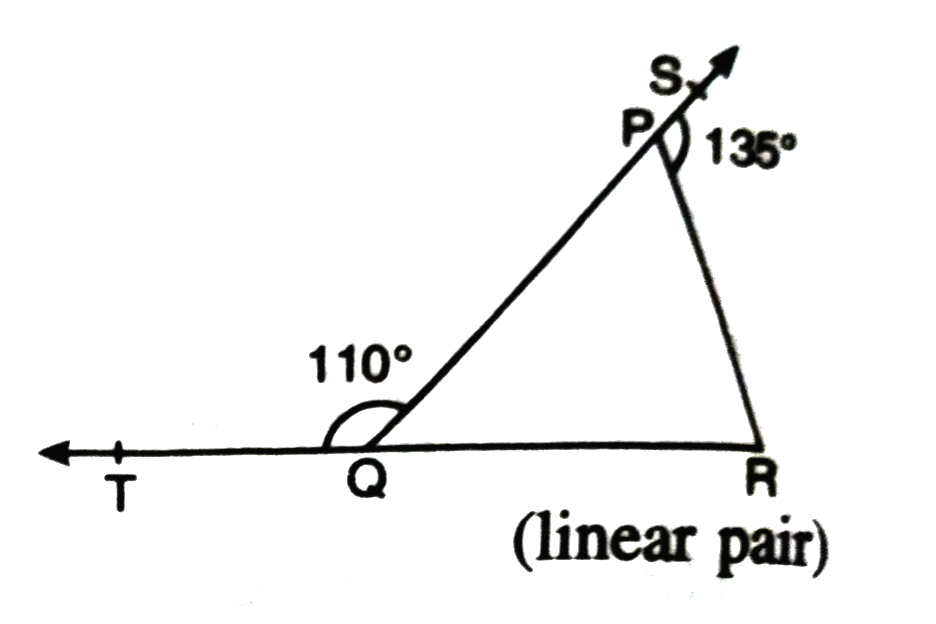
1. In the given fig., sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

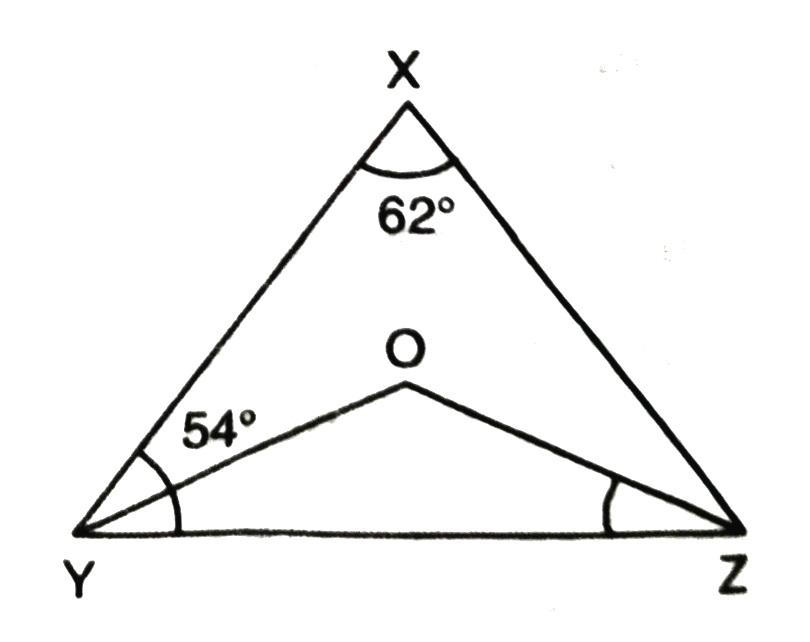
2. In the given fig., ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
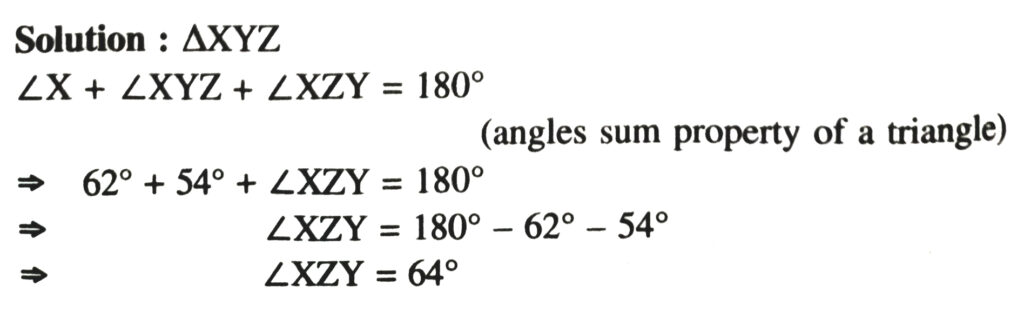
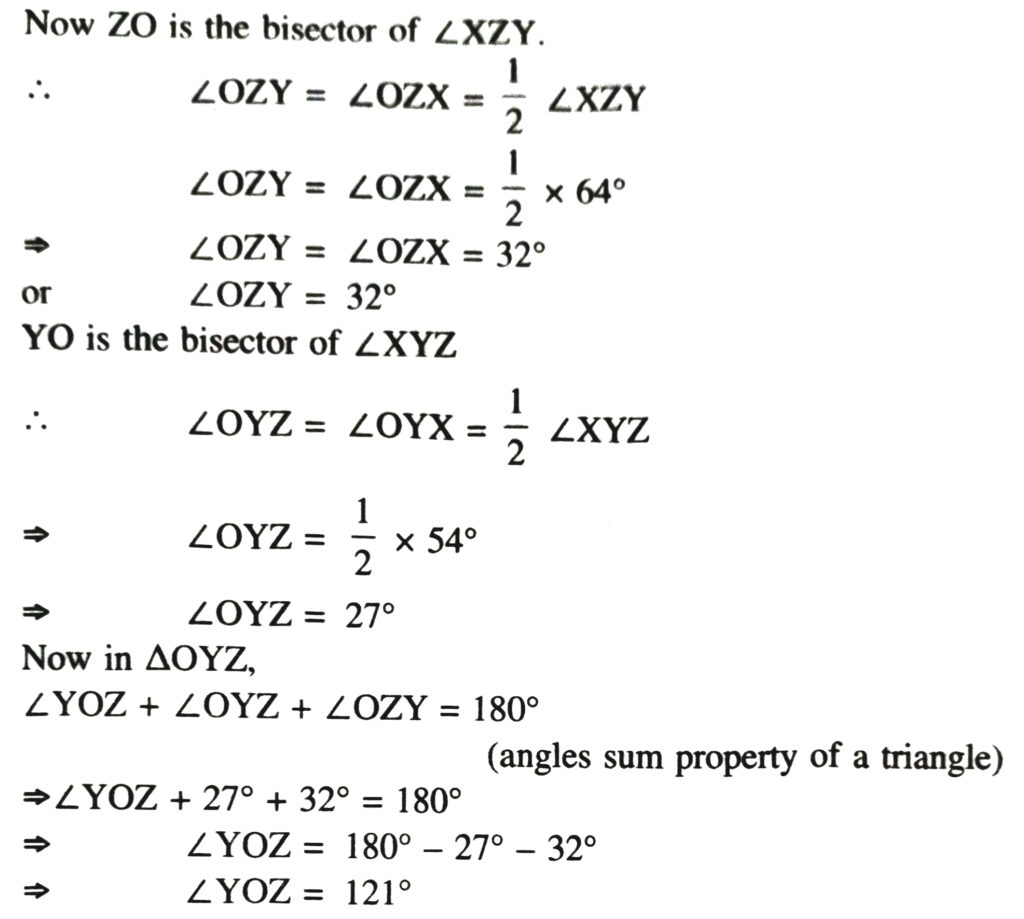
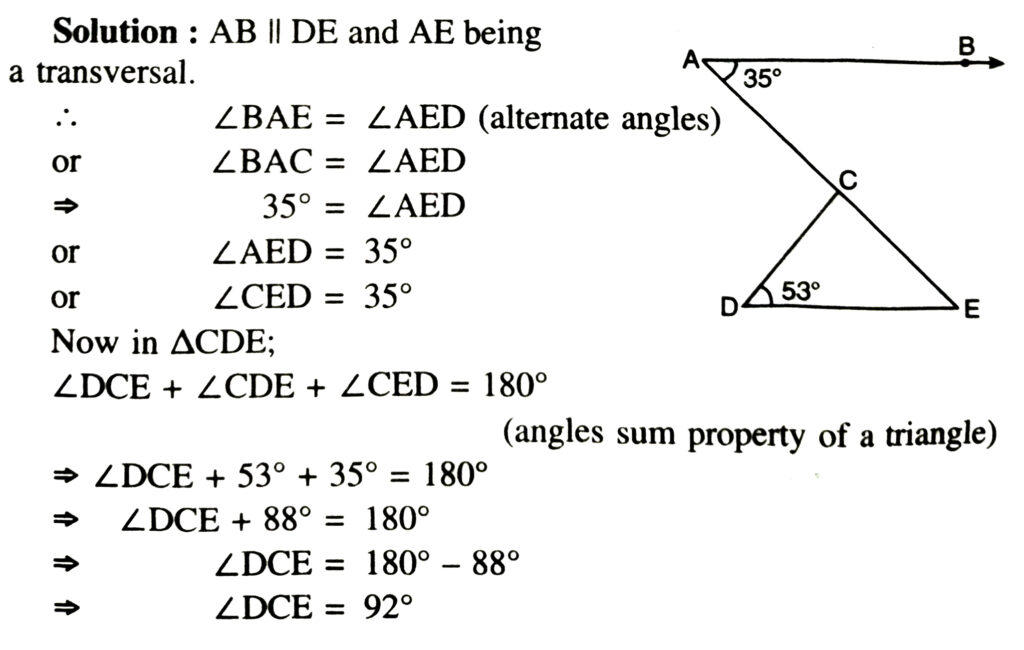
3. In the given Fig., if AB ΙΙ DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
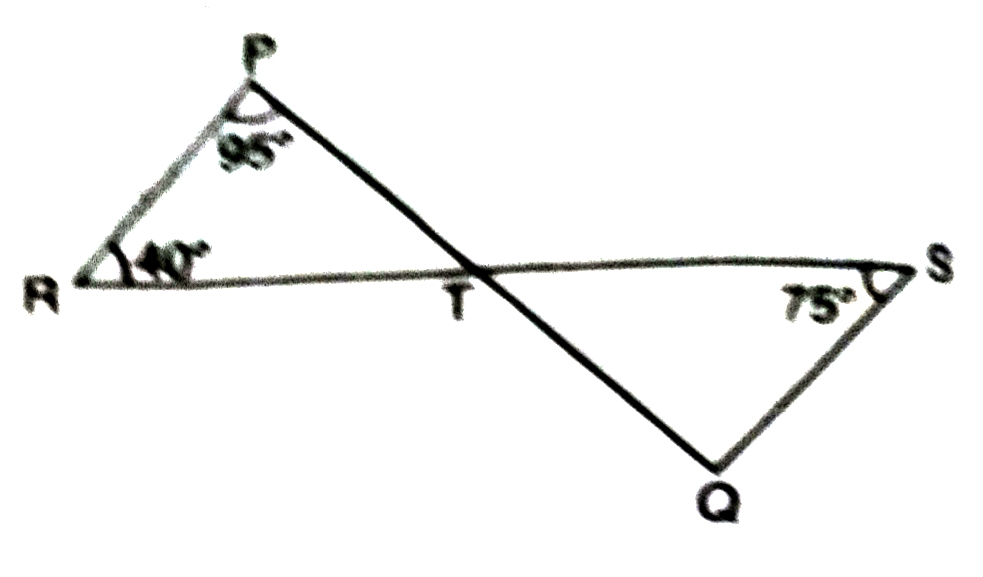
4. In the given Fig., if lines PQ and RS intersect at point T, such that ∠PRT=40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
Solution.—

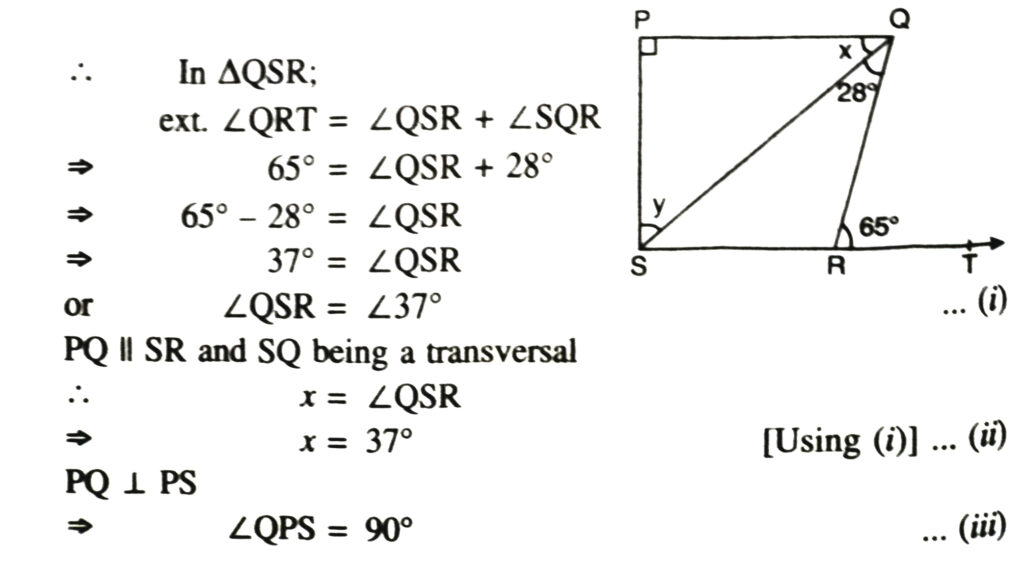
5. In the given Fig., if PQ ⊥ PS, PQ ΙΙ SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
Solution.— As we know that exterior angle of a triangle is equal to sum of its interior opposite angles.

6. In the given Fig., the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that
∠QTR = 1/2 ∠QPR.

Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here