JKBOSE 9th Class Mathematics Solutions Chapter 7 Triangles
JKBOSE 9th Class Mathematics Solutions Chapter 7 Triangles
JKBOSE 9th Class Mathematics Solutions Chapter 7 Triangles
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Triangles Textbook Questions and Answers
INTRODUCTION
You have studied about triangles and their various properties in your earlier classes. Triangle is a closed figure formed by three intersecting lines (‘Tri’ means ‘three’). A triangle has three sides, three angles and three vertices. For example, in triangle ABC, denoted as ΔABC (See Fig.) AB, BC, CA are the three sides, ∠A, ∠B, ∠C are the three angles and A, B, C are three vertices.
In Chapter 6, you have also studied some properties of triangles. In this Chapter, you will study in details about the congruency of triangles, rules of congruence, some more properties of triangles and inequalities in a triangle.
You have already verified most of these properties in earlier classes. We will now prove some of them.
CONGRUENCE OF TRIANGLES
Two triangles are congruent if one of them can be made to superpose on the other, so as to cover it exactly.
Suppose ΔABC is congruent of ΔEFG (see Figs.), then it is possible for us to superpose ΔABC on ΔEFG, so as to cover it exactly. Now in any such superimposition, the vertices of ΔABC will on the vertices of ΔEFG, in same order and then, each side of ΔABC, will superpose on the corresponding side of ΔEFG, so as to cover it exactly. Also, each angle of ΔABC, will superpose on the corresponding angle of ΔEFG, so as to cover it exactly. Thus, the order in which the vertices match automatically determines a correspondence between the sides and angles
of the two triangles. And if the superimposition is exact, we get six equalities, three of the corresponding sides and three of the corresponding angles.
Let us suppose, ΔABC superposes on ΔEFG, exactly when vertices of ΔABC fall on the vertices of ΔEFG, in the order.
A ↔ E, B ↔ F, C ↔ G
or in short ABC ↔ EFG
Then we have the equalities-
AB = EF, BC = FG, CA = GE
∠A = ∠E, ∠B = ∠F, ∠C = ∠G
Now we can always think of a matching (correspondence) between the vertices of two triangles of the type ABC ↔ EFG, whether or not it makes the superimposition with exact cover or not. If you try to think of all such matchings, you will observe that there are six such matching in all. These are :
ABC ↔ EFG, ABC ↔ FGE, ABC ↔ GEF
ABC ↔ EGF, ABC ↔ GFE, ABC ↔ FEG
If ΔABC is congruent to ΔEFG, one of these six possible matchings will lead to superposition with exact cover, and hence we will have three equalities of the lengths of corresponding sides and three equalities of the measures of corresponding angles. On the other hand, if ΔABC is not congruent of ΔEFG, then none of the six possible matchings will lead to superposition with exact cover. And, therefore, in each matching at least some one part of ΔABC will not be equal to the corresponding part of ΔEFG.
Hence, we obtain the following general condition of congruence of two triangles.
Two triangles are congruent, if and only if there exists a correspondence between their vertices such that the corresponding sides and the corresponding angles of the two triangles are equal.
Notation. If ΔABC is congruent to ΔEFG and the correspondence ABC ↔ EFG makes the six parts of corresponding part of the two triangles congruent, then we write
ΔABC ≅ ΔEFG
From the manner the two triangles are named, we can easily infer the six equalities between the corresponding parts of the two congruent triangles. We shall use the symbol “c.p.c.t.” to indicate corresponding parts of congruent triangles.
CONGRUENCE RELATION IN THE SET OF ALL TRIANGLE
The definition of congruence of triangles and the notation above, immediately lead to the following results :
(i) If ΔABC ≅ ΔEFG, then,
ΔERG ≅ ΔABC
(ii) If ΔABC ≅ ΔEFG,
and ΔEFG ≅ ΔPQR then ΔABC ≅ ΔPOR
Obviously we also have
(iii) ΔABC ≅ ΔABC
Axiom : S.A.S. (Side-Angle-Side)
Congruence Axiom : Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other.
This axiom refers to two sides and the angle between them, so it is known as (side-angle-side) or the “SAS Congruence Axiom” or the n SAS Criterion”.
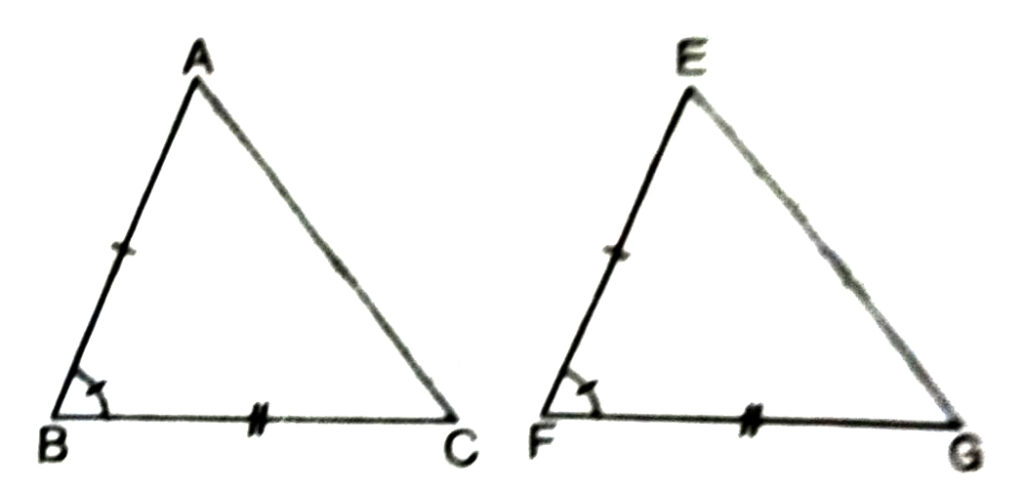
Thus in the Fig. shown above AB = EF, BC = FG and ∠B = ∠F, then
ΔABC ≅ ΔEFG (i.e. CA = GE, ∠A = ∠E, ∠C = ∠G would also be true.
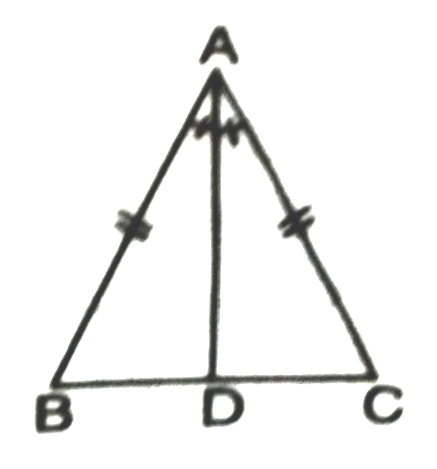
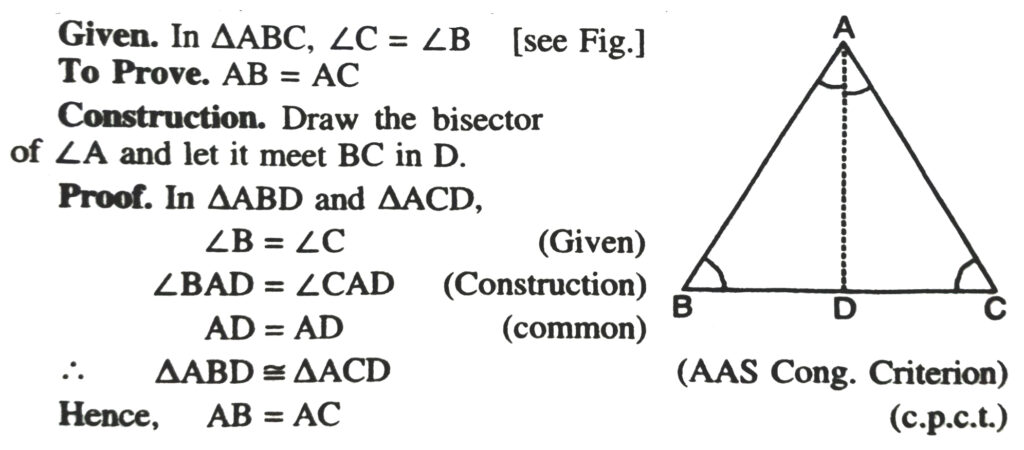
Theorem 1. Angles opposite to two equal sides of a triangle are equal.
Given. In ΔABC, AB = AC (see fig.)
To prove. ∠C = ∠B
Construction. We draw the bisector AD of ∠A which meets BC in D.
Proof. In Δs ABD and ACD,
AB = AC (given)
∠BAD = ∠CAD (construction)
AD = AD (common side)
∴ ΔABD ≅ ΔACD (SAS Congruence Axiom)
Hence, ∠B = ∠C (c.p.c.t.)
Theorem 2. ASA (Angle-Side-Angle) congruence theorem. Two triangles are congruent, if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
Given. In Δs ABC and PQR,
∠B = ∠Q
∠C = ∠R
BC = QR
To prove. ΔABC ≅ ΔPQR
Case. I. If AB=PQ, then ΔABC will be congruent to ΔPQR by the SAS Criterion, and the theorem is proved.
Case II. Suppose AB ≠ PQ and suppose AB is less than PQ. Take a point S on PQ such that QS = AB.
Join RS
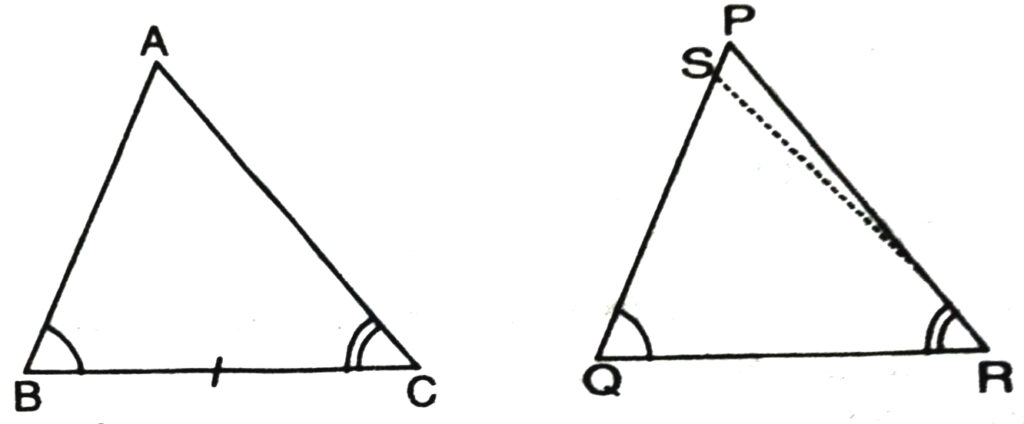
In Δs ABC and SQR,
AB = SQ (Supposed)
BC= QR (Given)
∠B = ∠Q (Given)
∴ ΔABC ≅ ΔSQR (SAS Criterion)
Hence, ∠ACB = ∠QRS (c.p.c.t.)
∠ACB = ∠QRP (Given)
∴ ∠QRP = ∠QRS
which is impossible unless ray RS coincides with ray RP or S coincides with P.
∴ AB must be equal to PQ
Case III. If we suppose that AB is greater than PQ, then a similar argument apples and ΔABC ≅ ΔPQR
Hence, in all cases, ΔABC ≅ ΔPQR.
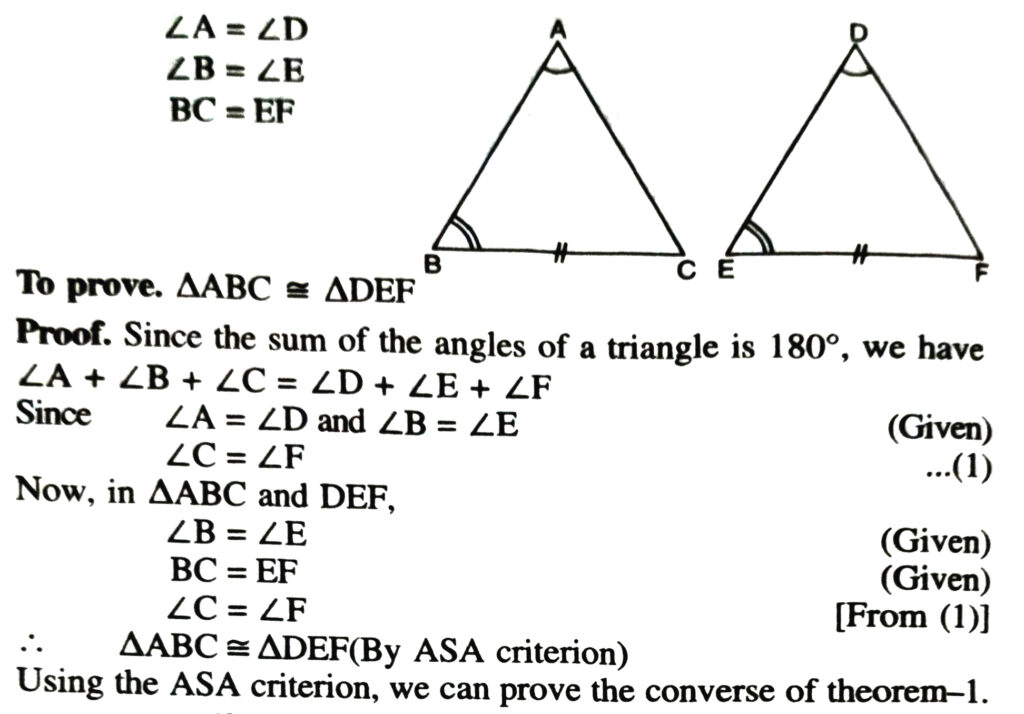
COROLLARY (AAS Congruence Criterion)
If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
Given. In Δ’s ABC and DEF (see Fig.)
Theorem 3. If two angles of a triangle are equal, then the sides opposite to them are also equal.
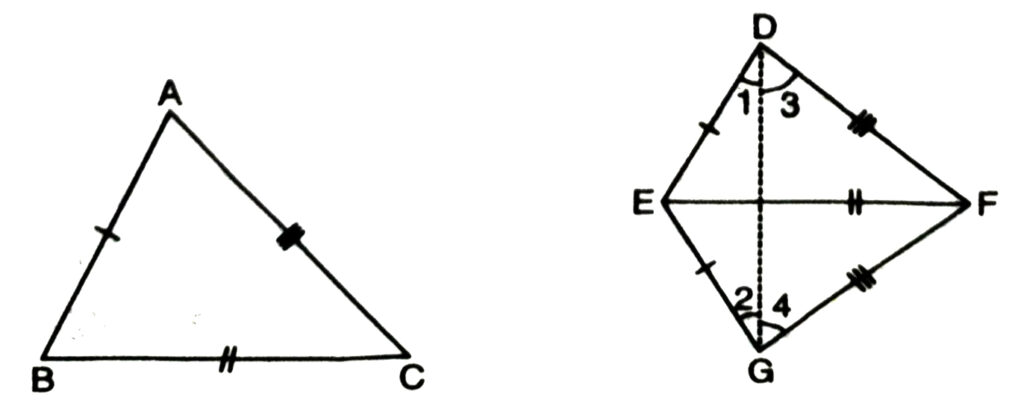
Theorem. 4. SSS (Side-Side-Side) Congruence Theorem. Two triangles are congruent, if the three sides of one triangle are equal to the corresponding three sides of the other triangles.

TEXT BOOK EXERCISE – 7.1
1. In quadrilateral ABCD (See Fig.), AC = AD and AB bisects ∠A. Show that ΔABC ≅ ΔABD.
What can you say about BC and BD ?

2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. (See, Fig.) Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
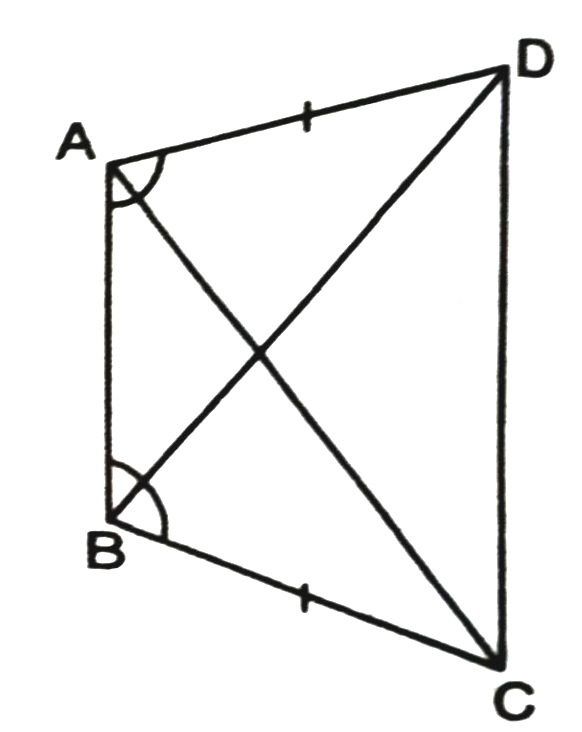
Solution.— In ΔBOC and ΔABC,
AD = BC (given)
∠DAB = ∠CBA (given)
AB = AB (common)
∴ ΔABD ≅ ΔBAC (SAS Criteria of congruency)
⇒ BD = AC (Congruent parts of congruent triangles)
and ∠ABD = ΔBAC (Congruent parts of congruent triangles)
3. AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB (See. Fig.)
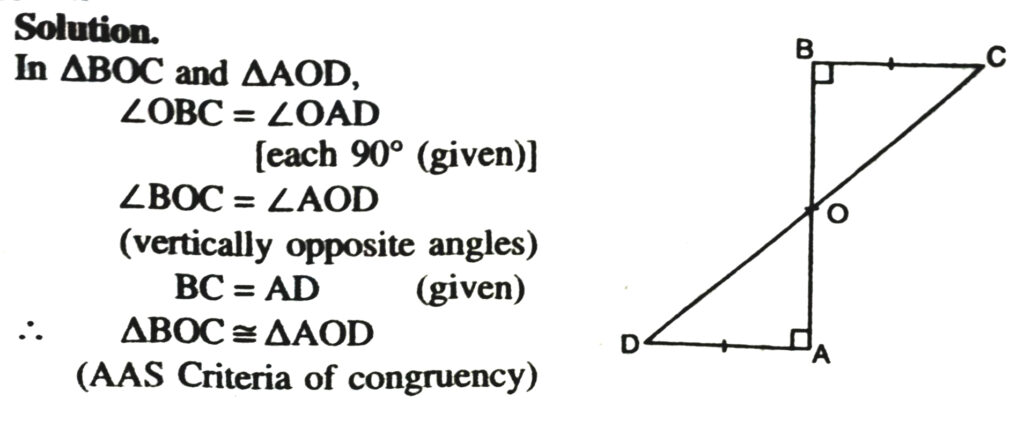
⇒ OB = OA
and OC = OD (Congruent parts of congruent triangles)
It implies that O is the mid-point of line-segment AB and CD.
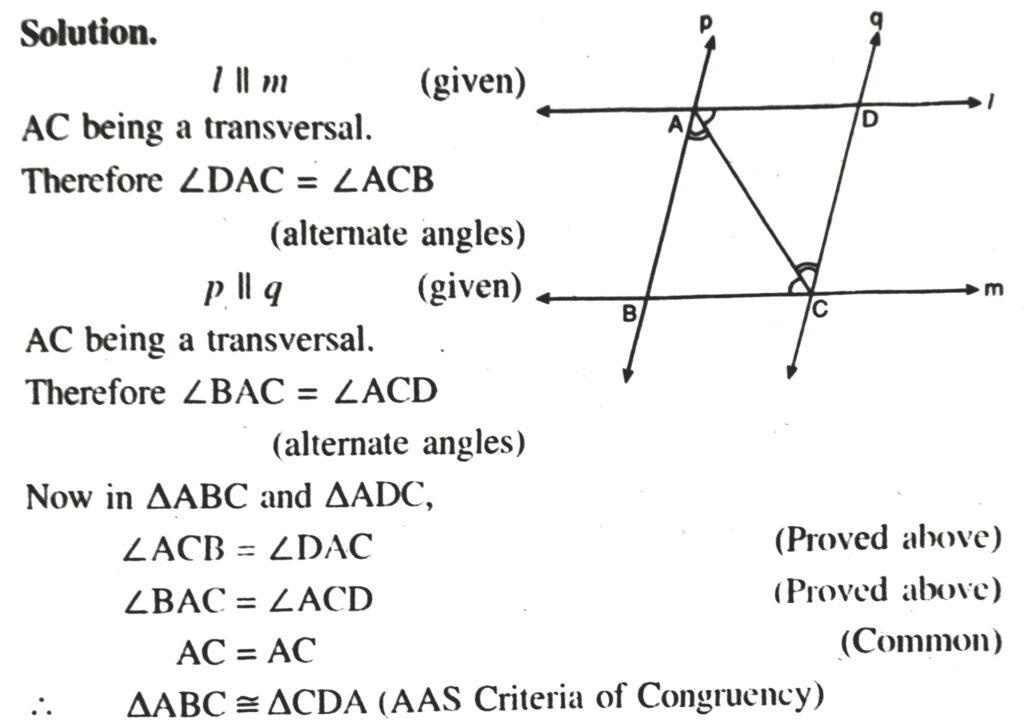
4. l and m are two parallel lines intersected by another pair of parallel lines p and q (See Fig.) Show that ΔABC ≅ ΔCDA.
5. Lines l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A . Show that :
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A (see Fig.)
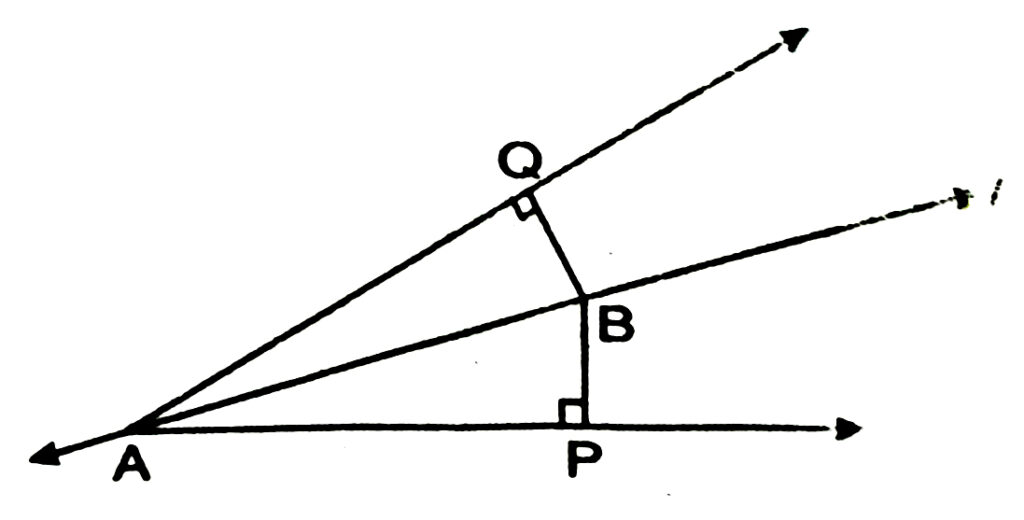
Solution.— Given that line l bisects ∠A.
∴ ∠BAP = ∠BAQ
Now in ΔΑΒΡ and ΔΑΒΟ,
∠BAP = ∠BAQ (given)
∠BPA = ∠BQA [each 90º (given)]
AB = AB (common)
∴ ΔAPB ≅ ΔAQB (AAS Criteria of Congruency)
⇒ BP = BQ (Congruent parts of congruent triangles)
i.e B is equidistant from the arms of ∠A.
6. In Fig., AC = AE , Ab = AD and ∠BAD = ∠EAC. Show that BC = DE.
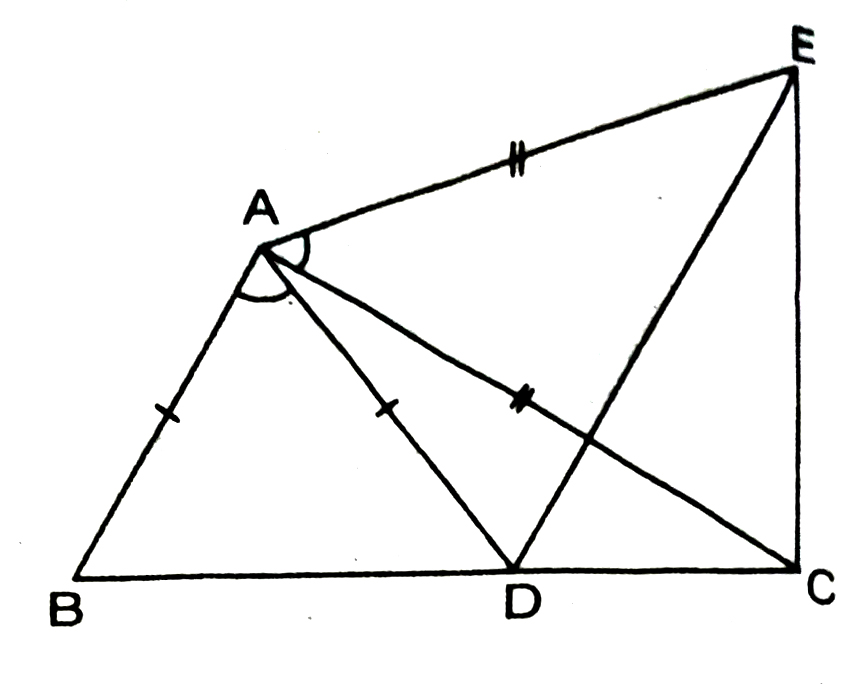
Solution.— Give that
∠BAD = ∠EAC
Adding ∠DAC on both sides, we get :
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠EAD …(i)
Now in ΔABC and ΔAED,
AB = AD (given)
AC = AE (given)
∠BAC = ∠ DAE [from (i)]
∴ ΔABC ≅ ΔADE (AAS Criteria of Congruency)
⇒ BC = DE (Congruent parts of Congruent triangles)
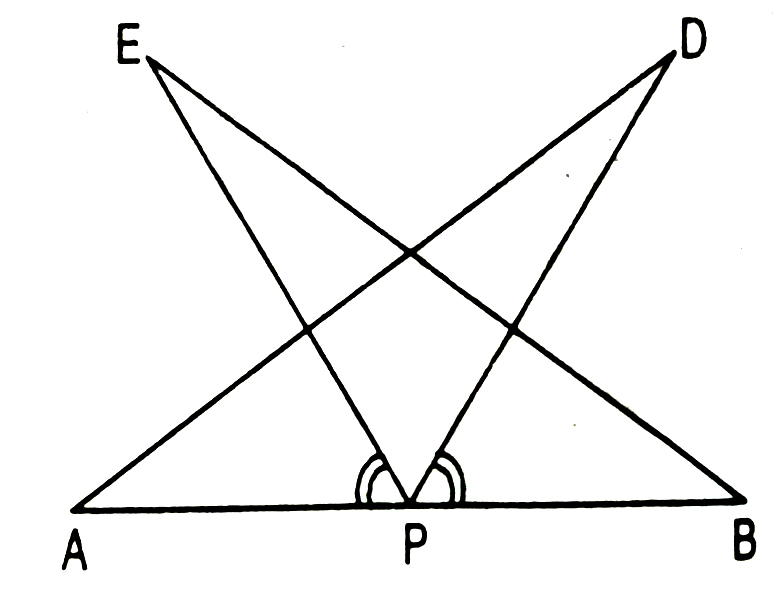
7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE AND ∠EPA = ∠DPB. Show that
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE (See Fig.)


8. In right triangle ABC, right angled at C, M is the mind-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig.) Show that :


Properties of Triangle
In the theorems 1 and 3 of this section we have proved that
◆ Angle opposite to two equal sides of a triangle are equal.
◆ If two angles of a triangle are equal, then the sides opposite to them are also equal.
◆ In this section we shall deal with those problems based on congruency of triangles in addition to the above properties.
TEXT BOOK EXERCISE – 7.2
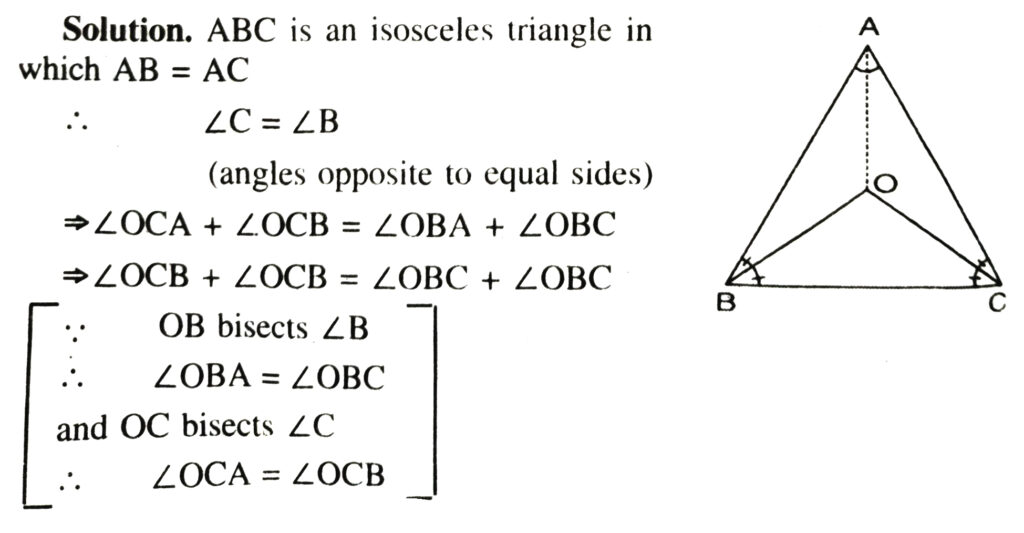
1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O show that :
(i) OB = OC (ii) AO bisects ∠A.

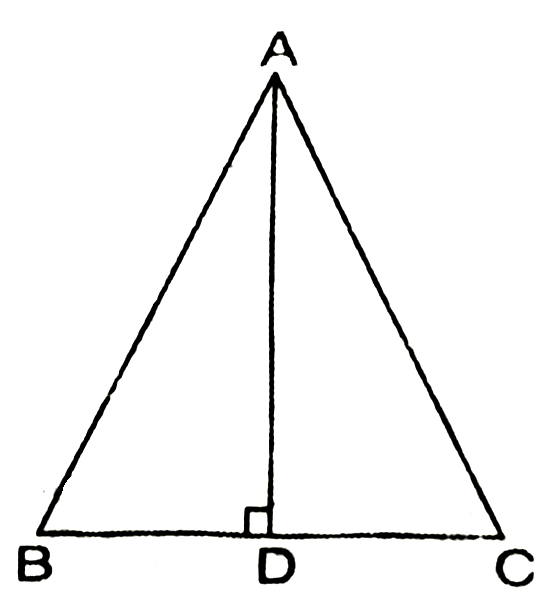
2. In ΔABC, AD is the perpendicular bisector of BC (See Fig.). Show that ΔABC is an isosceles triangle in which AB = AC.

3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.). Show that these altitudes are equal.
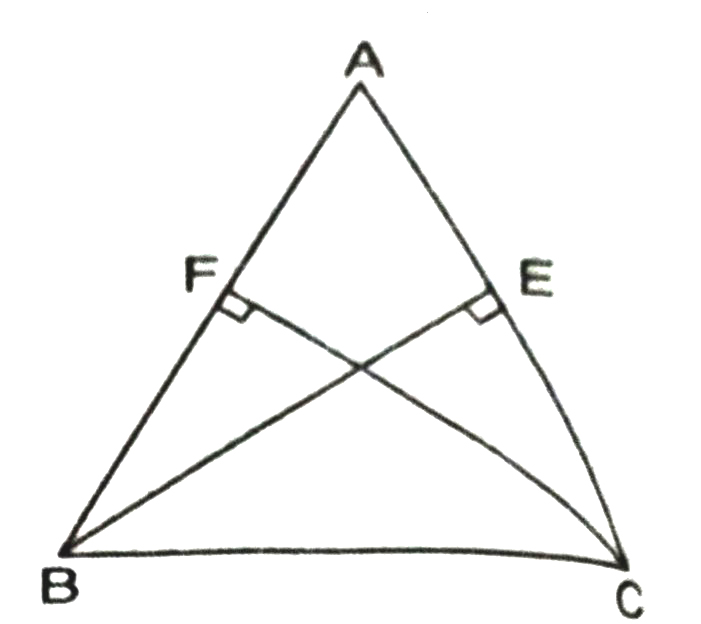

4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See Fig.). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC or ΔABC is an isosceles triangle.
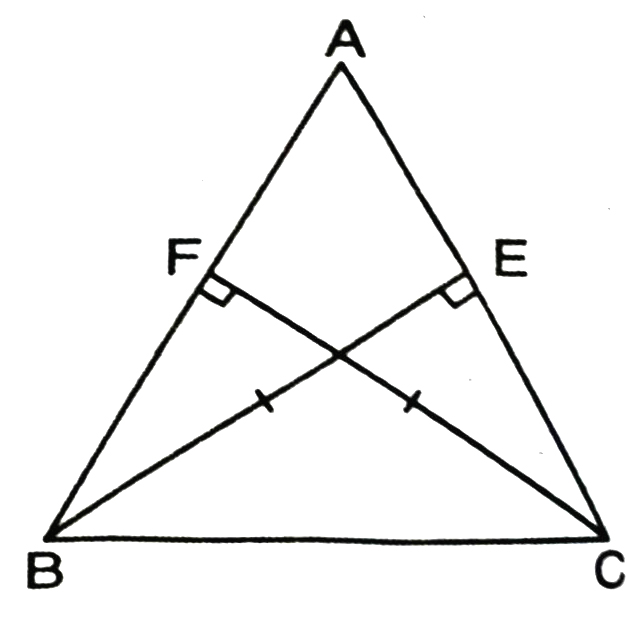
5. ABC and DBC are two isosceles triangles on the same base BC (See Fig.). Show that ∠ABD = ∠ACD.
Solution.— In isosceles ΔABC,
AB = AC (given)
∴ ∠ACB = ∠ABC …(i)
(angles opposite to equal sides)
Also in isosceles ΔBCD,
BD = DC
∴ ∠BCD = ∠CBD …(ii)
(angles opposite to equal sides)
Adding corresponding sides of (i) and (ii),
∠ACB + ∠BCD = ∠ABC + ∠CBD
⇒ ∠ACD = ∠ABD
or ∠ABD = ∠ACD (proved)
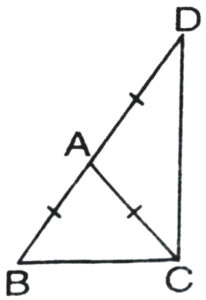
6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that ∠BCD is a right angle (see Fig.).


7. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠.C.
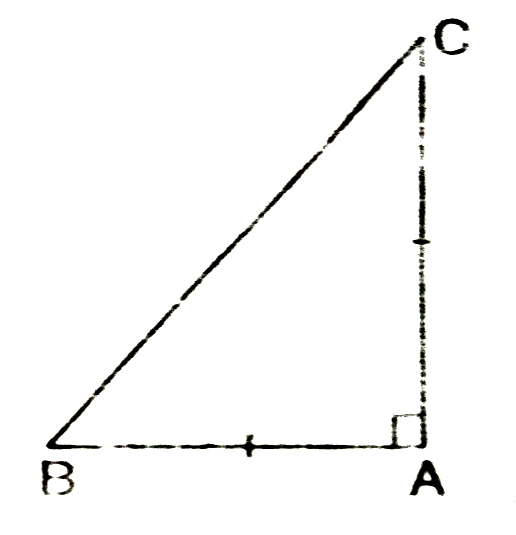

⇒ C = 45º
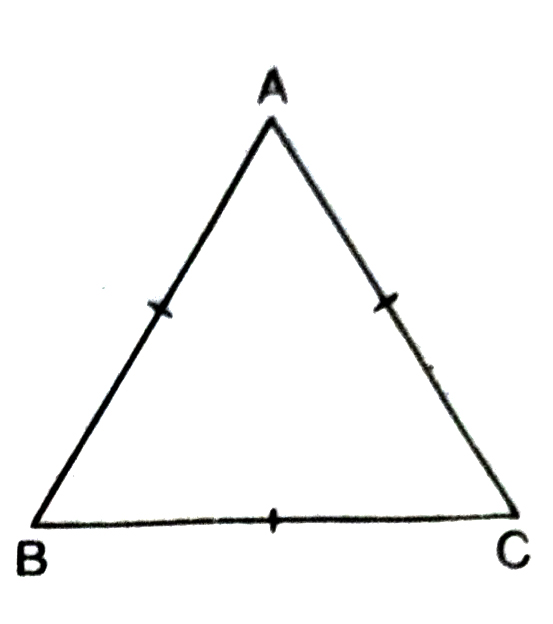
8. Show that the angles of an equilateral triangle are 60° each.

Theorem 5. RHS (Right Angle-Hypotenuse Side) Congruence Theorem.
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and the corresponding side of the other triangle.
Given. In ΔABC and DEF (See fig.)

TEXT BOOK EXERCISE – 7.3
1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
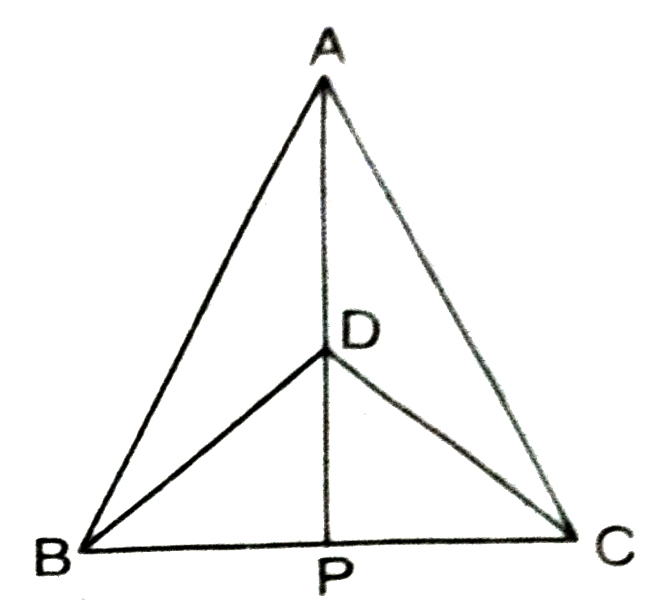


From (e), we have BP = PC and from (g), we have proved AP ⊥ BC. So, collectively we can say that AP is perpendicular bisector of BC.
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
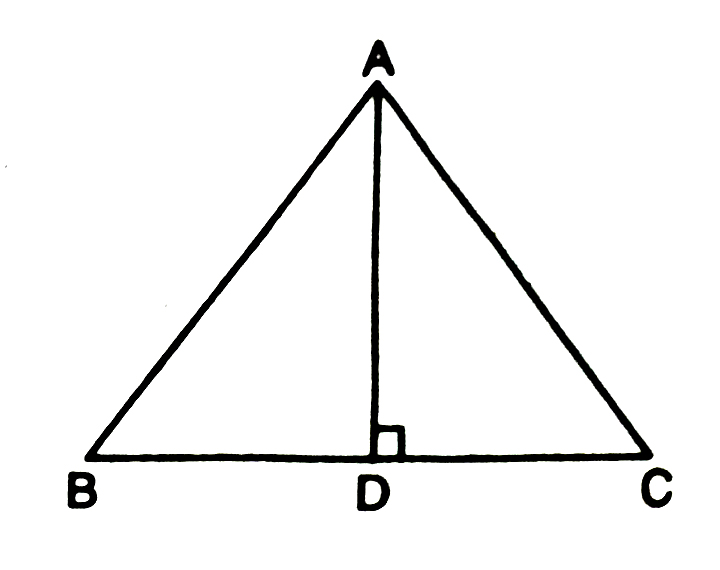
Solution.— In ΔABD and ΔACD,
AB = AC (given)
∠ADB = ∠ADC (each = 90º)
[∴ AD ⊥ BC (given)]
AD = AD (common)
∴ ΔABD ≅ ΔACD (RHS rule of congruency)
So, BD = DC (congruent parts of congruent triangles)
It implies AD; bisects BC (Proved part (i))
Also ∠BAD = ∠CAD (Congruent parts of congruent triangles)
It implies AD bisects ∠A.
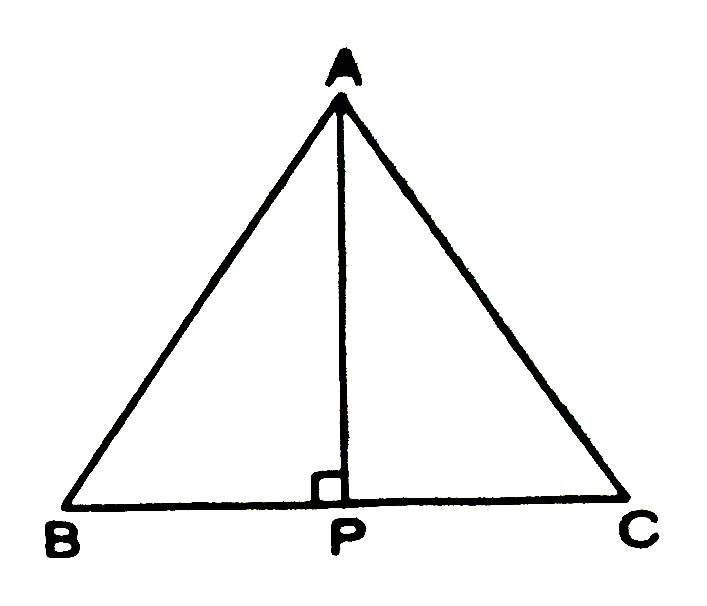
3. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC and show that ∠B = ∠C.

INEQUALITIES IN A TRIANGLE
You have been studying about congruence and equality, in this chapter so far. Sometimes, we do come across unequal objects and the need to compare them.
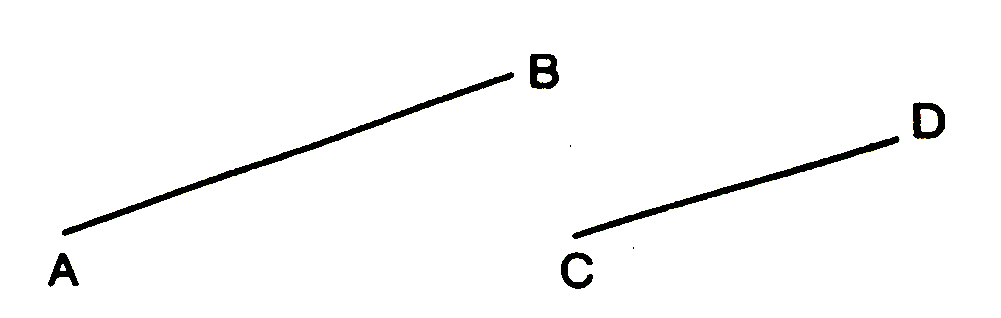
For example, line segment AB is greater in length as compared to line segment CD [see fig. (i)].
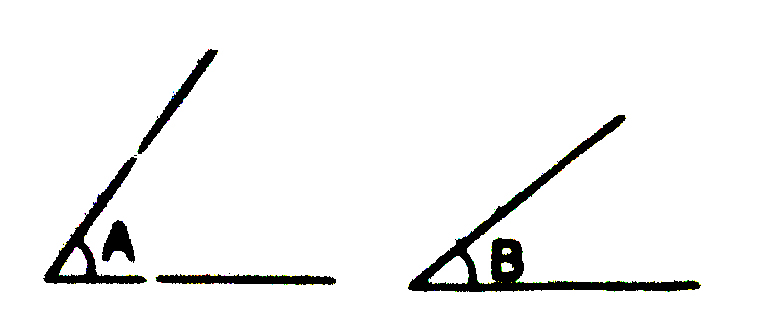
∠A is greater than ∠B see fig (ii)
Let us now examine whether there is any relation between unequal sides and unequal angles of a triangle. For this, perform the following activity:
Construct a scalene triangle (that is a triangle in which all sides are of different lengths). Measure the lengths of the sides. Now, measure the angles. What do you observe ?
In ΔABC of Fig., BC is the longest side and AC is the shortest side. Also, ∠A, is the largest and ∠B is the smallest.
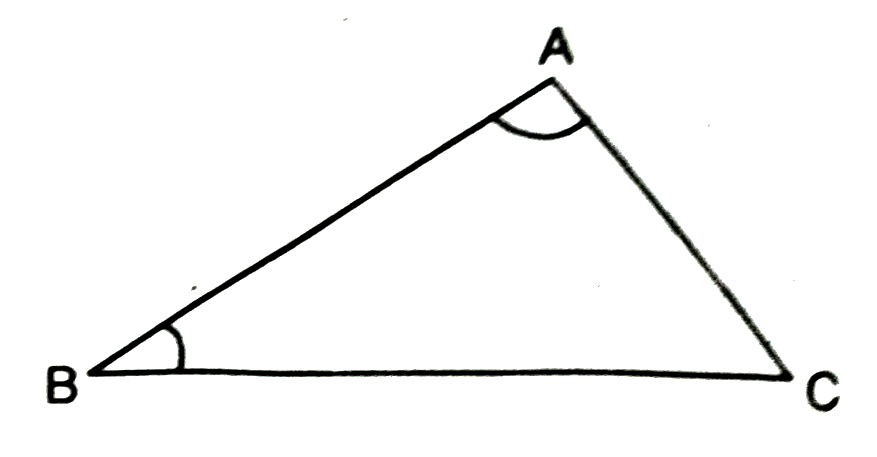
Repeat this activity with other triangles.
We arrive at a very important result of inequalities in a triangle. It is stated in the form of a theorem as shown below :
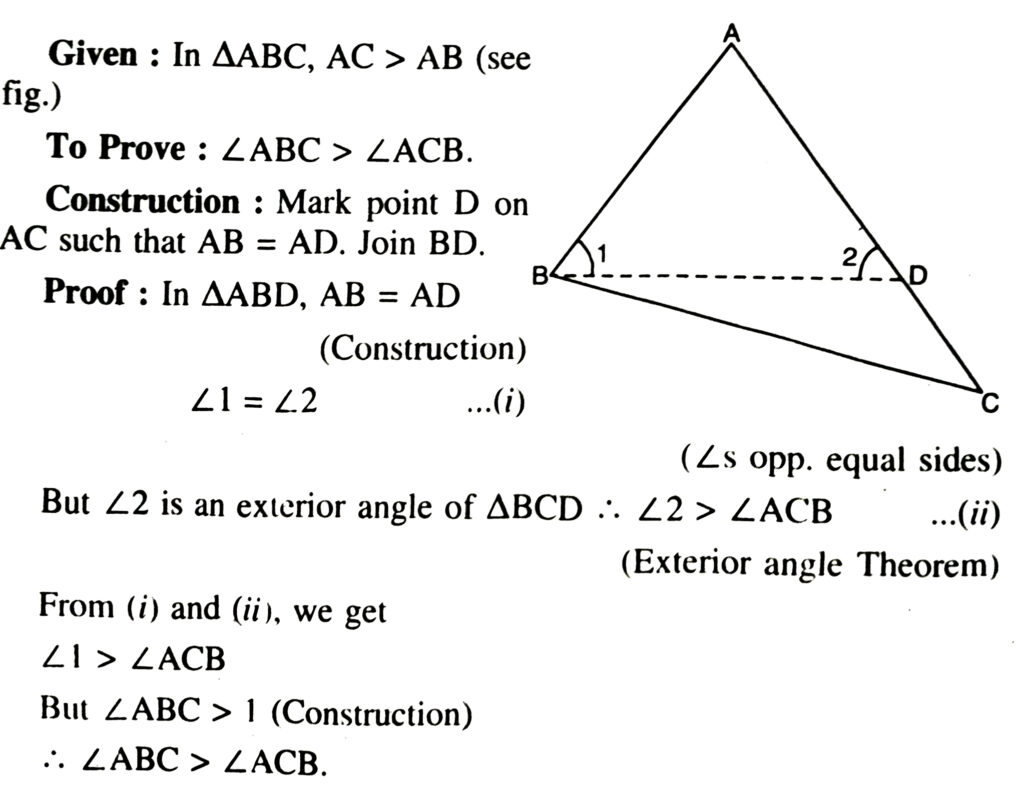
Theorem. If two sides of a triangle are unequal, the longer side has greater angle opposite to it.
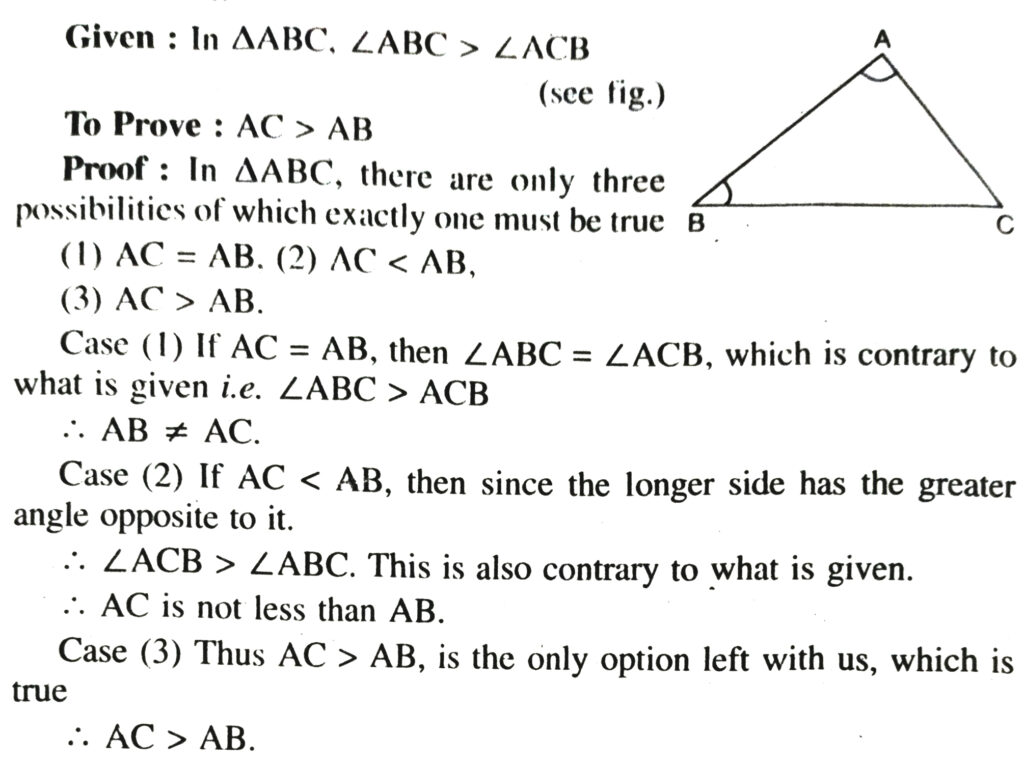
Theorem: In a triangle, the greater angle has the longer side opposite to it.
Theorem. The sum of any two sides of a triangle is greater than the third side.
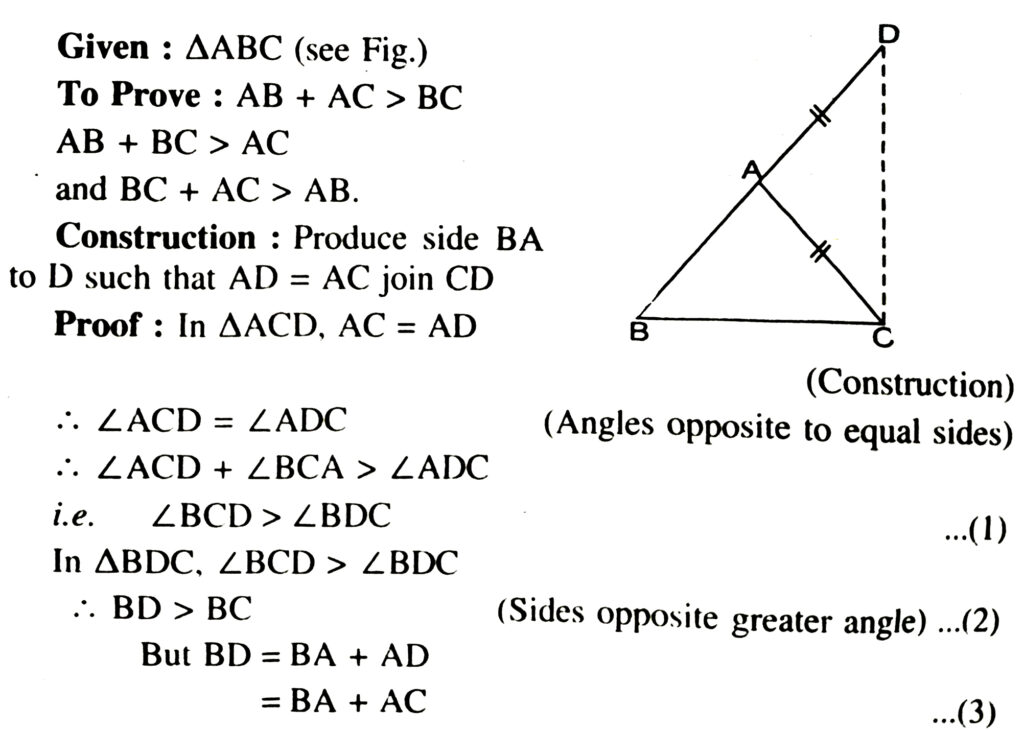
From (2) and (3), we get
BA + AC > BC
Similarly, we can prove that
AB + BC > AC AND BC + AC > AB.
TEXT BOOK EXERCISE – 7.4
1. Show that in a right angled triangle, the hypotenuse is the longest side.

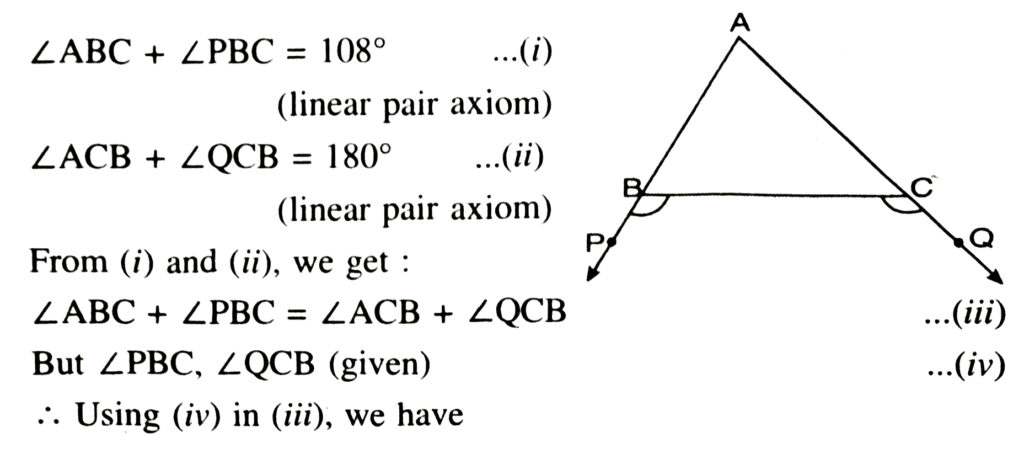
2. In Fig., sides AB and AC of ΔABC are extended to points P and Q respectively. Also ∠PBC < ∠QCB. Show that AC > AB.
Solution :

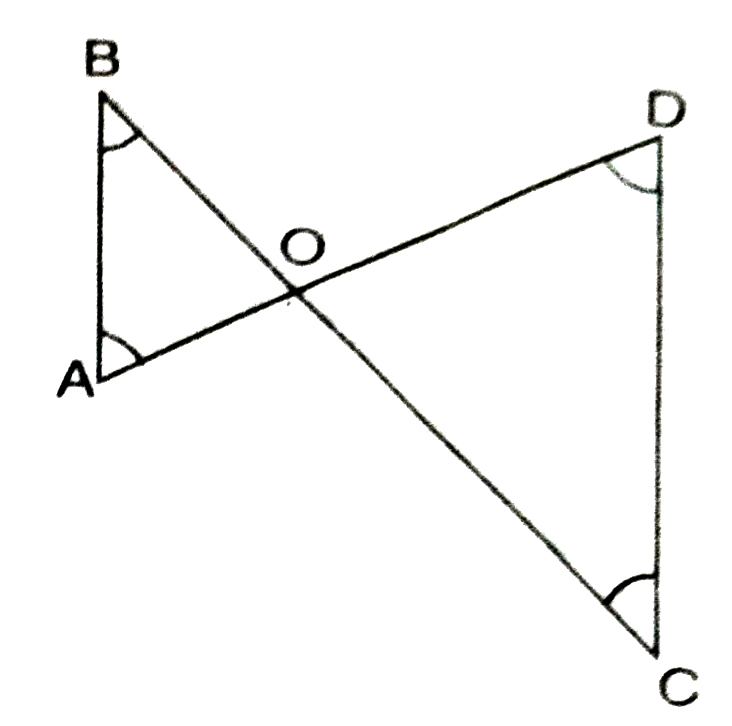
3. In Fig., ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

4. In Fig., PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.
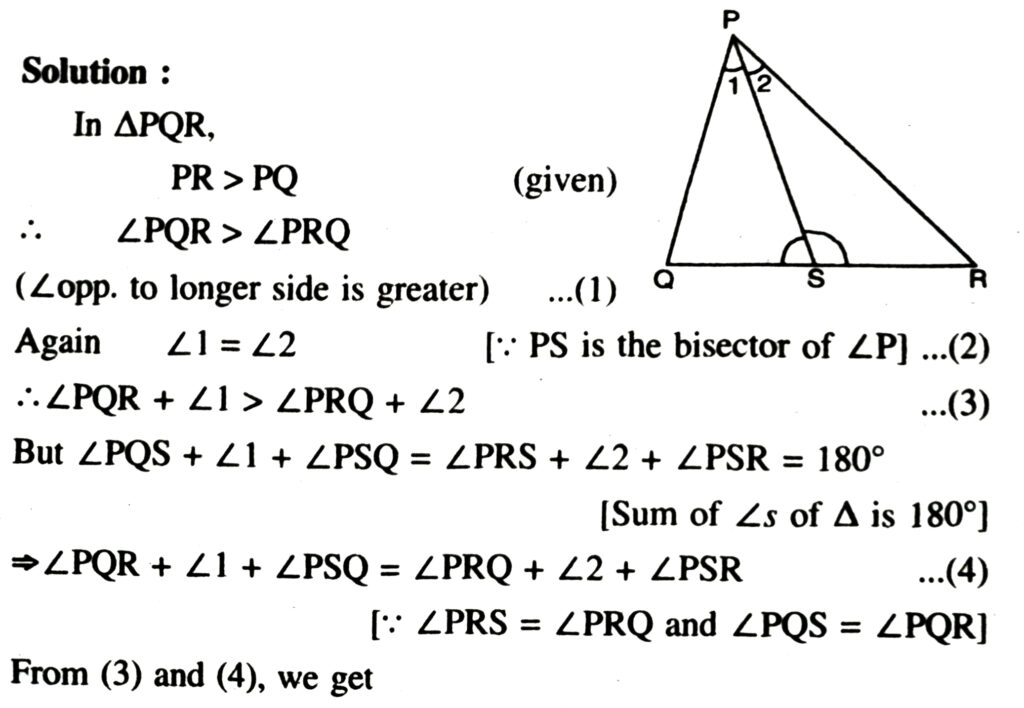
∠PSQ < ∠PSR
or ∠PSR > ∠PSQ
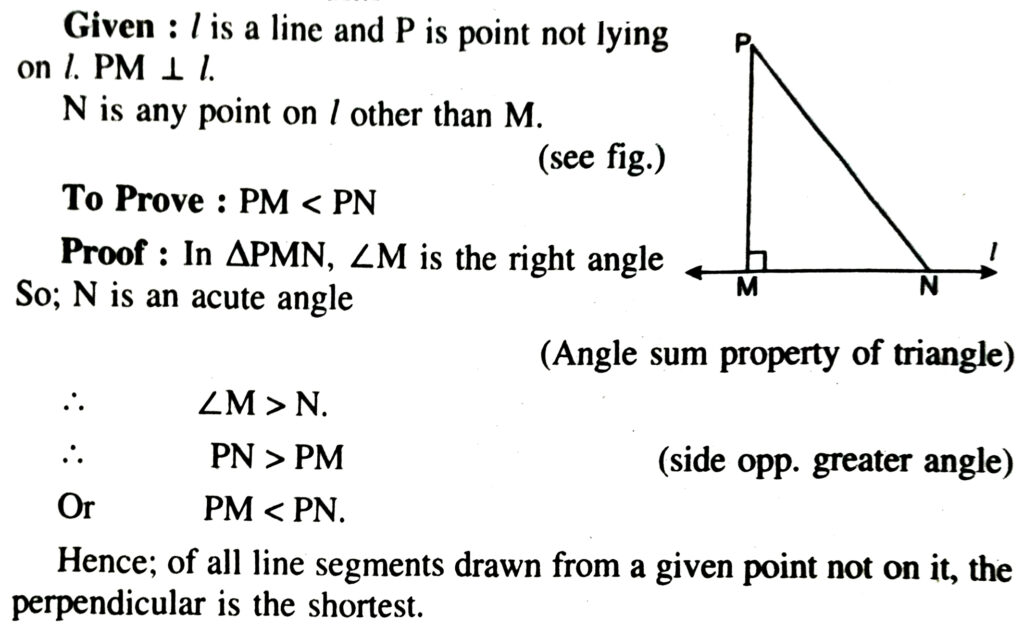
5. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here