JKBOSE 9th Class Mathematics Solutions Chapter 8 Quadrilaterals

03/25/202303/26/2023 keshav kumar 134 Views 0 Comments

Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions

J&K class 9th Mathematics Quadrilaterals Textbook Questions and Answers

INTRODUCTION

In the previous class, we had learnt quadrilaterals, special types of quadrilaterals such as trapezium, parallelogram and their properties. Further studied the special types of parallelogram such as rectangle, rhombus and square and their properties.

In this chapter, we shall prove those properties and solve the problems using these properties.

Properties of a Parallelogram—

Theorem 1. Opposite sides are equal in a parallelogram.

Theorem 2. The opposite angles of a parallelogram are equal.

Theorem 3. The two diagonals of a parallelogram bisect each other.

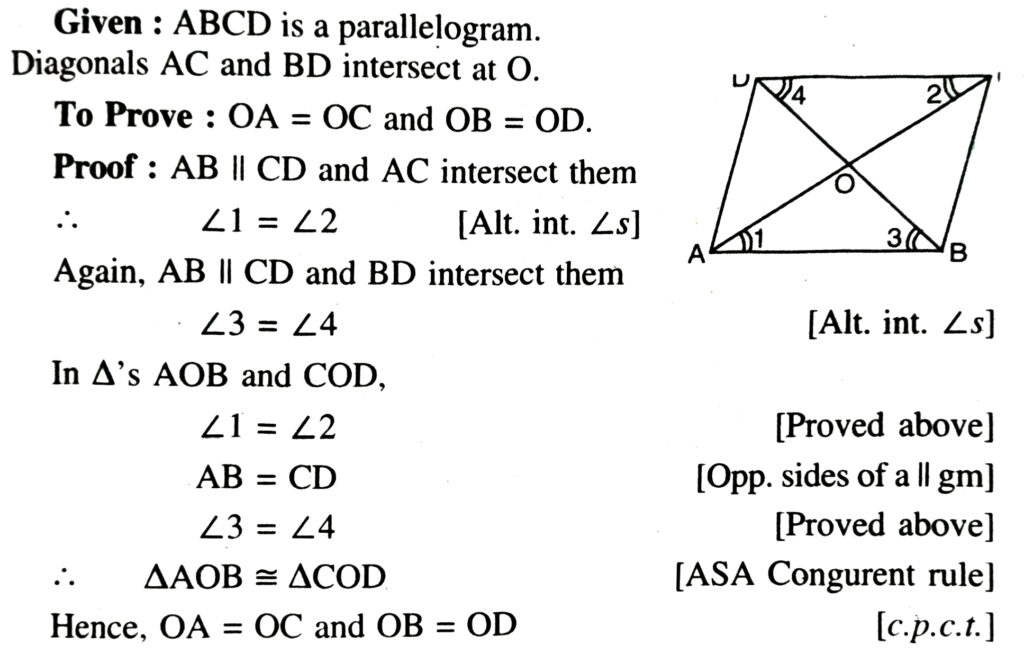
MUST REMEMBER—

1. Opposite sides of a parallelogram are equal.

2. The opposite angles of a parallelogram are equal.

3. The diagonals of a parallelogram bisect each other.

CONDITIONS FOR A QUADRILATERAL TO BE A PARALLELOGRAM

Theorem 4. (Converse of Theorem 1)-A quadrilateral is a parallelogram if its opposite

sides are equal.

Theorem 5. (Converse of a theorem 2)-A quadrilateral is a parallelogram if opposite angles are equal.

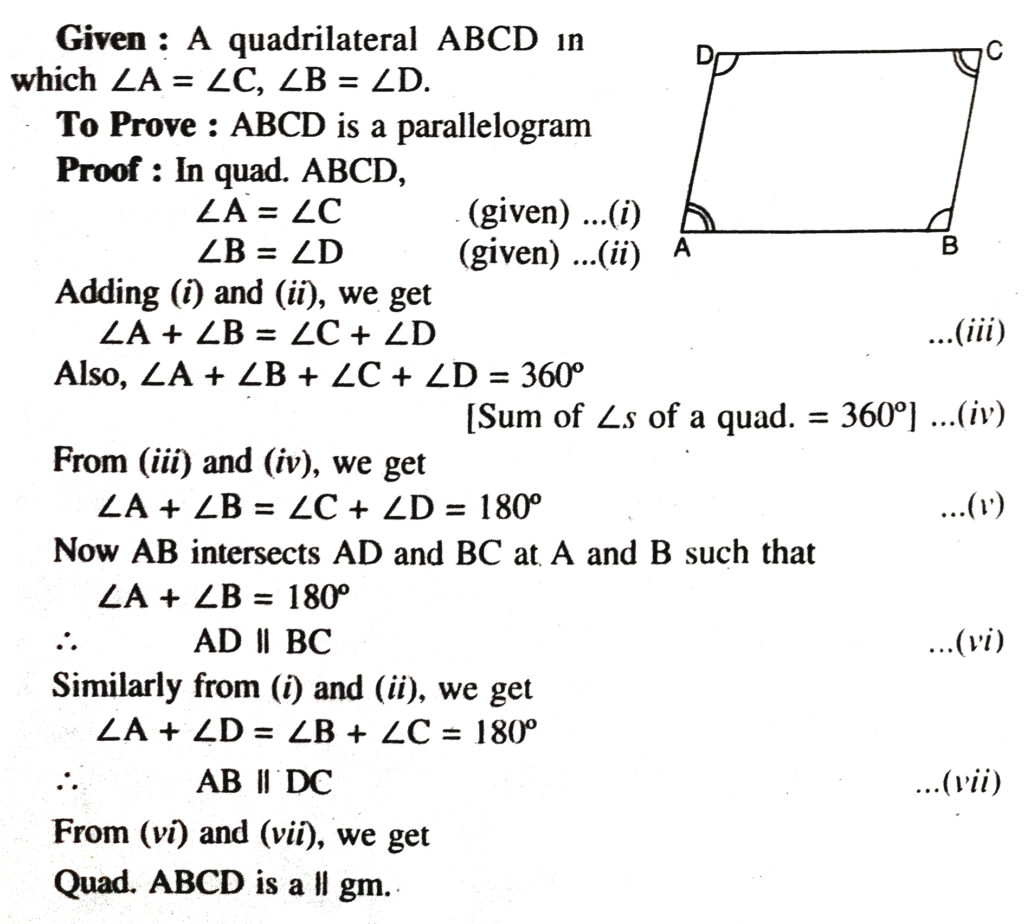
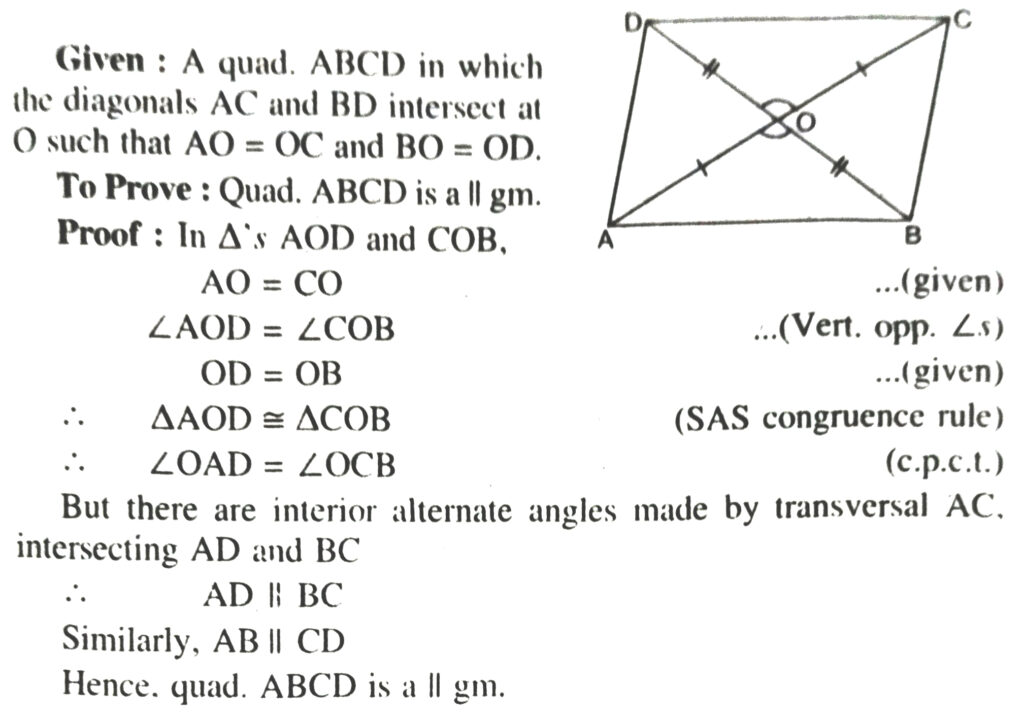
Theorem 6. (Converse of Theorem 3). If the diagonals of a quadrilateral bisect each other, then quadrilateral is a parallelogram.

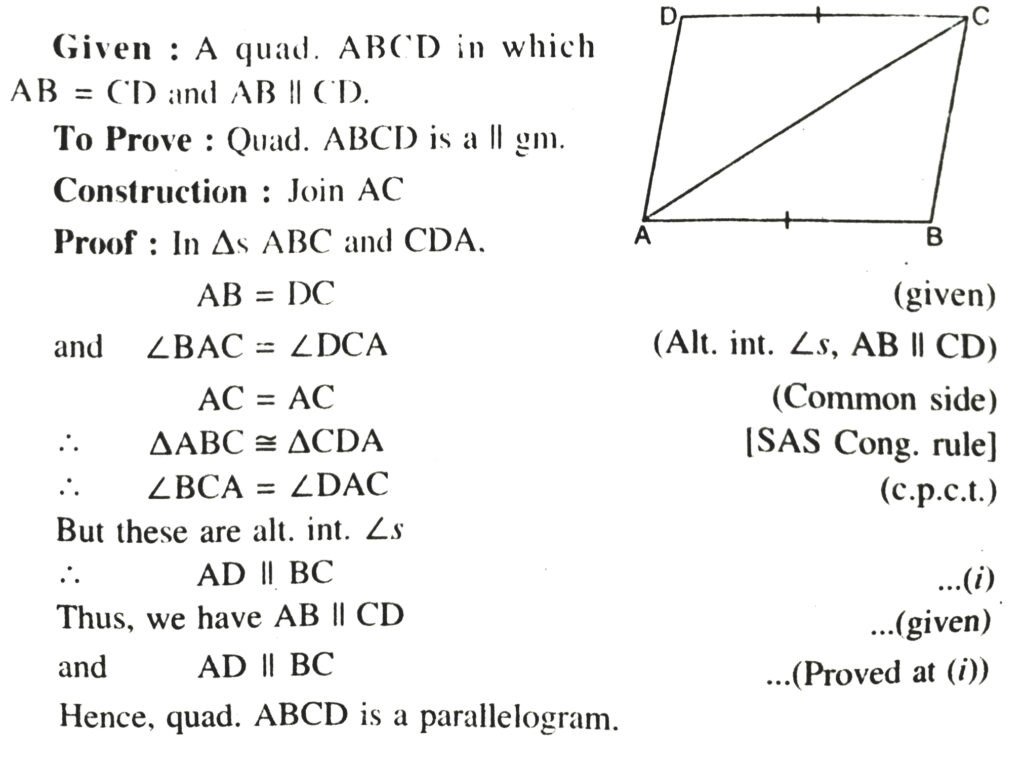
Theorem 7. A quadrilateral is a parallelogram, if its one pair of opposite sides are equal and parallel.

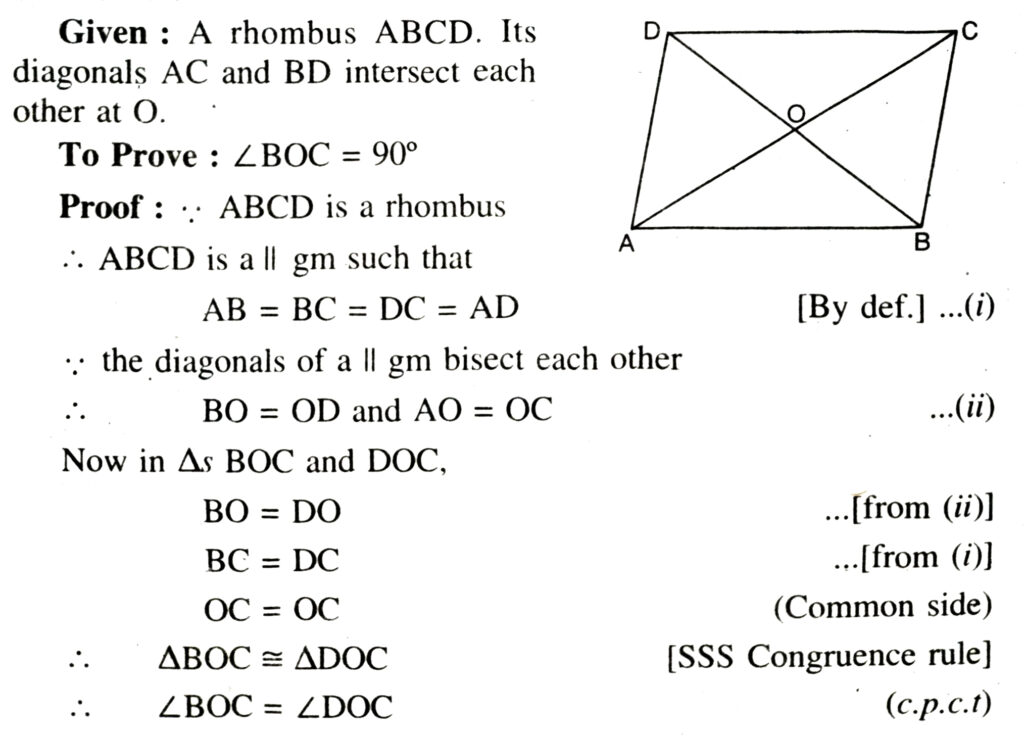
Theorem 8. The diagonals of a rect-angle are the equal length.

Theorem 9. The diagonals of a rhombus each other.

MUST REMEMBER—

1. A quadrilateral is a parallelogram, if its opposite sides are equal.

2. A quadrilateral is a parallelogram, if opposite sides are equal.

3. If a diagonal of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.

4. A quadrilateral is a parallelogram, if its one pair of opposite sides is equal and parallel.

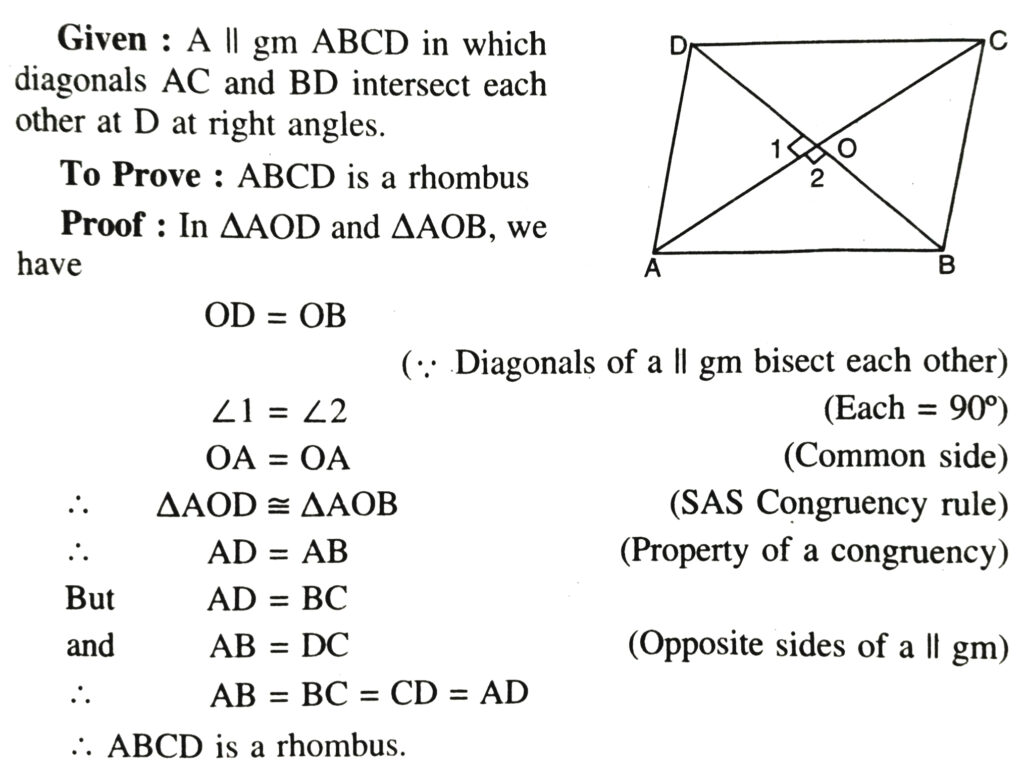
Theorem 10. If the diagonals of a parallelogram are perpendicular, then it is a rhombus.

COROLLARY-If in a parallelogram the diagonals are equal and perpendicular, then it is a square.

MUST REMEMBER—

1. The diagonals are equal of a rectangle.

2. The diagonals are perpendicular to each other in case of a rhombus.

3. The diagonals in case of a square are equal and perpendicular to each other.

4. When the diagonals are equal of a parallelogram it is a rectangle.

5. If the diagonals of a parallelogram are perpendicular, then it is a rhombus.

6. If in a parallelogram the diagonals are equal and perpendicular then it is a square.

TEXT BOOK EXERCISE – 8.1

1. The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all angles of the quadrilateral.

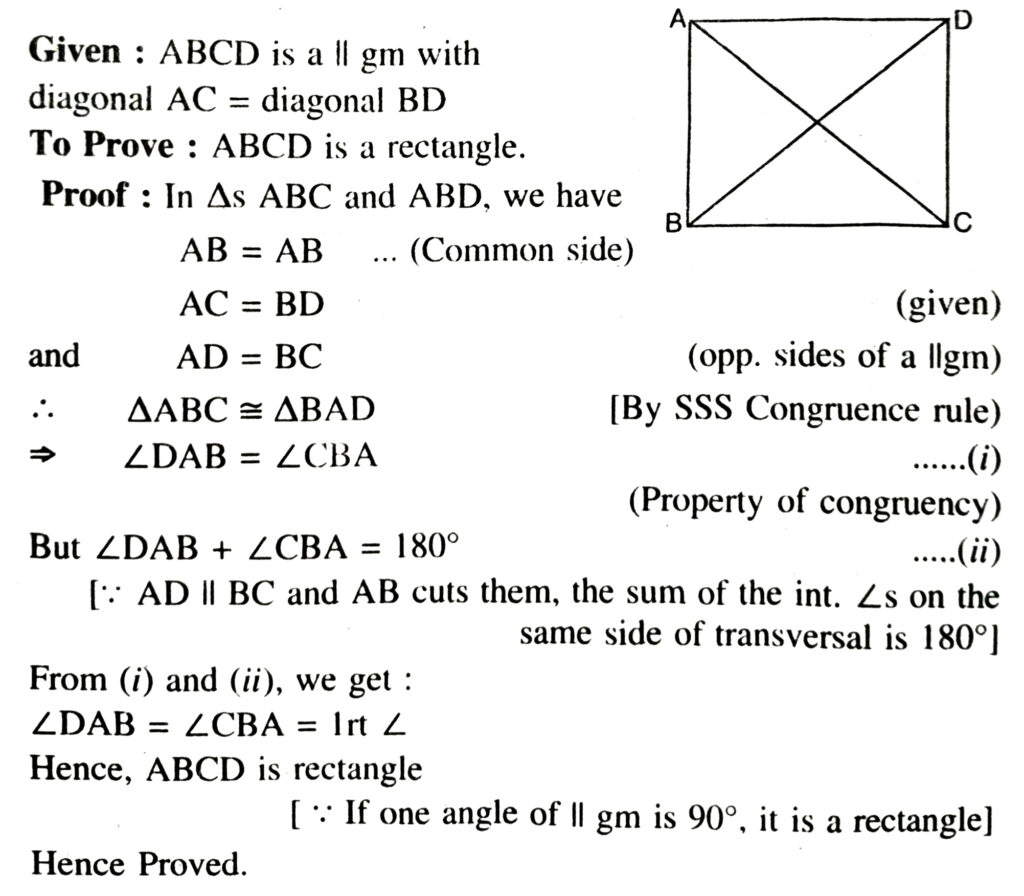
2. If the diagonals of a parallelogram are equal, show that it is a rectangle.

3. Show that if diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

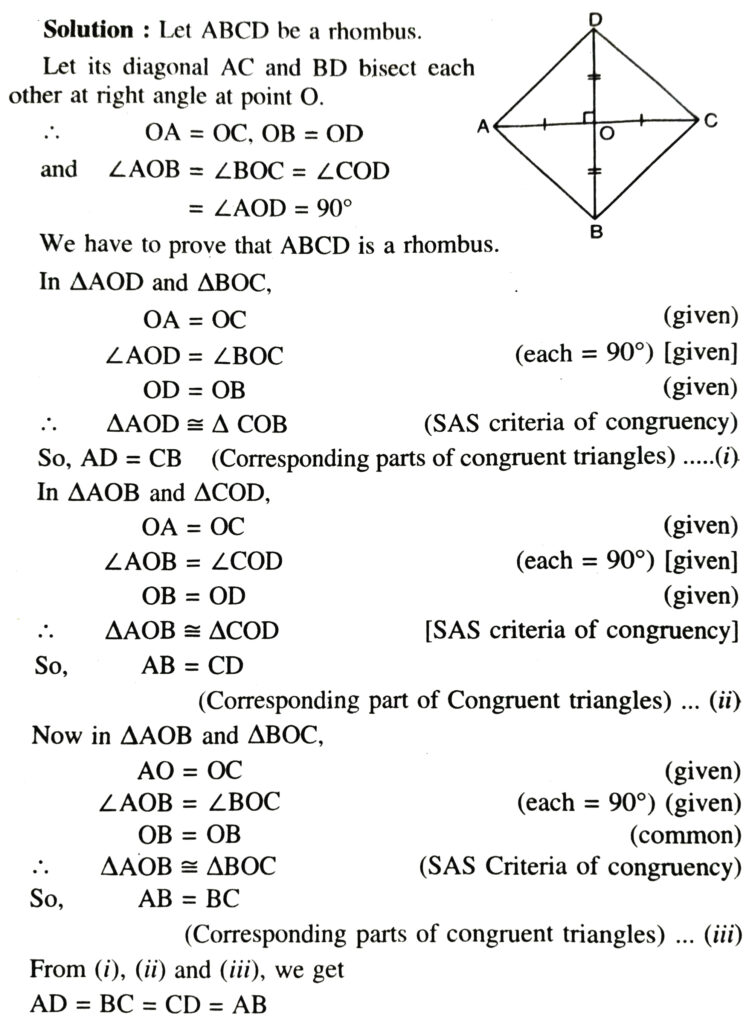
So, in addition to given conditions that the diagonals of a quadrilateral bisect each other at right angle; we also have all its sides equal. Hence quadrilateral satisfies all the conditions to be a rhombus Therefore given quadrilateral is a rhombus.

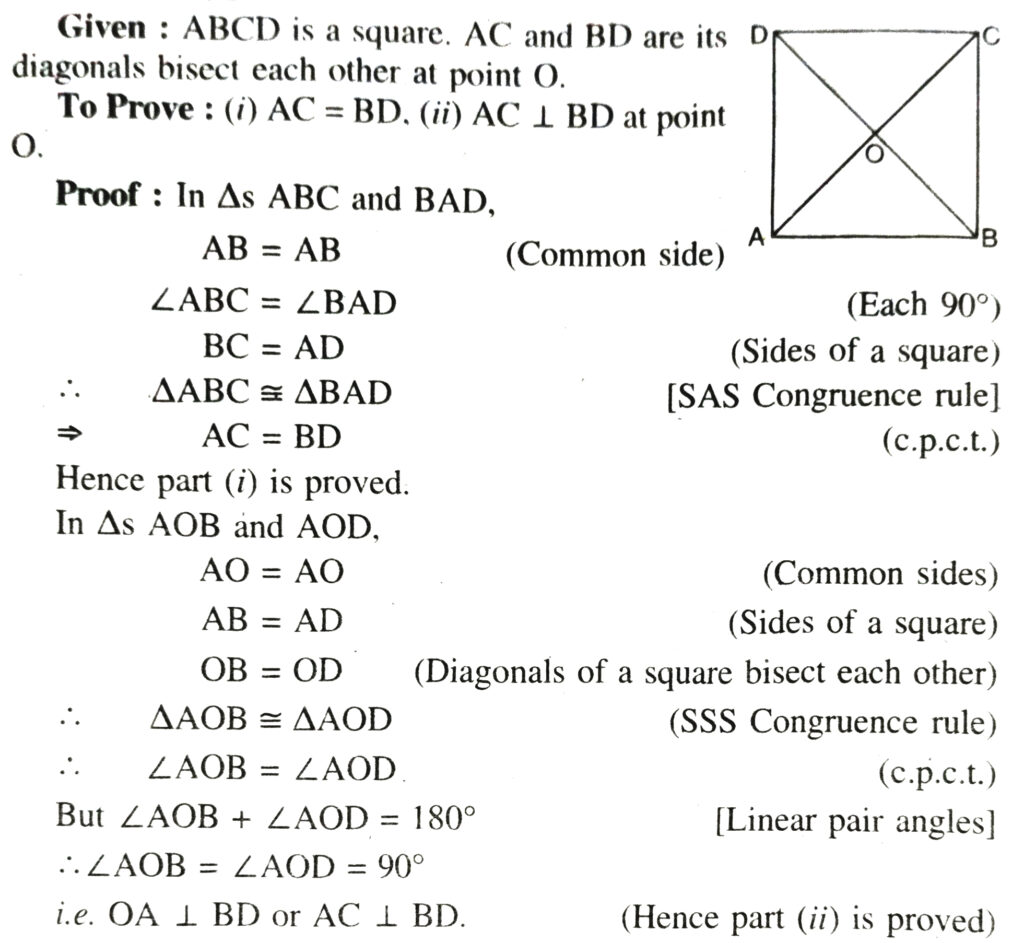
4. Show that the diagonals of a square are equal and bisect each other at right angles.

5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

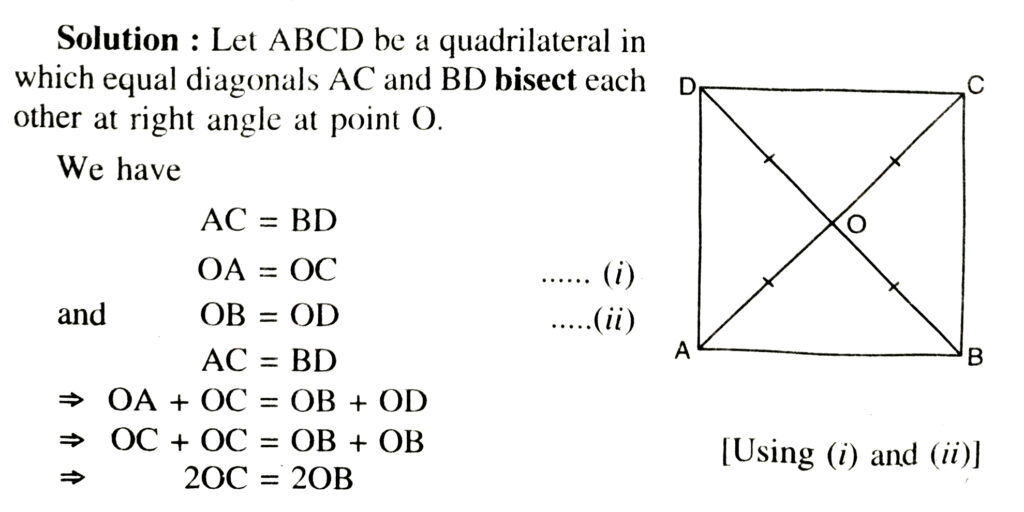
From (v), (vi) and (xiii) we get :

AB = BC = CD = AD …(xiv)

Using (xii) and (xiii), we get :

Now we have the quadrilateral whose equal diagonals bisect each other at right angle.

Also sides are equal make an angle of 90° with each other Hence given quadrilateral satisfy all conditions to be a square.

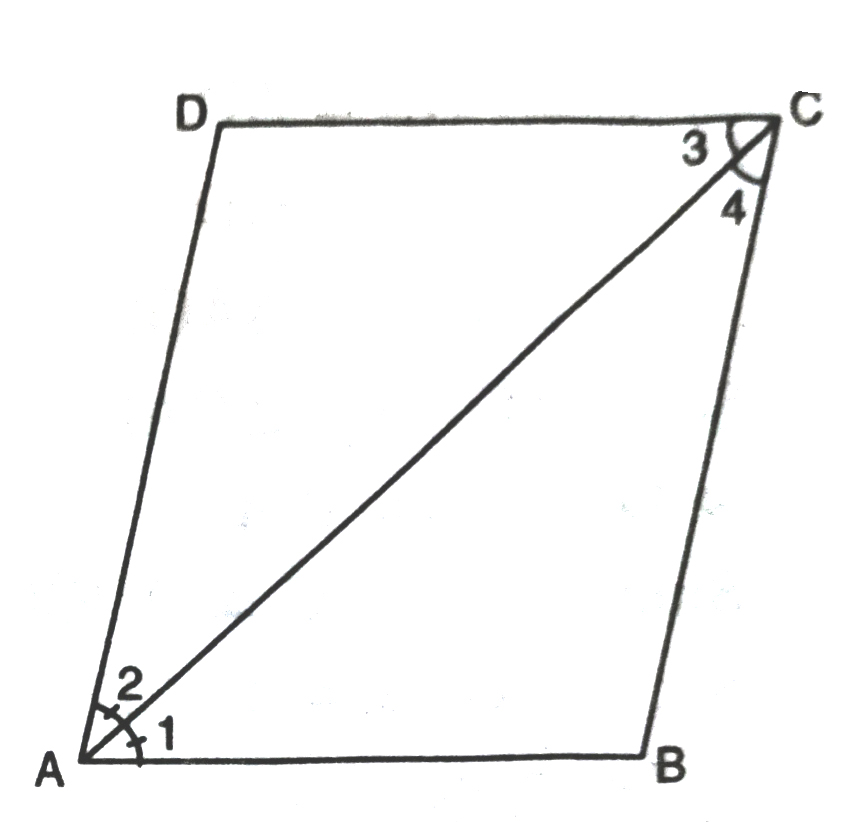
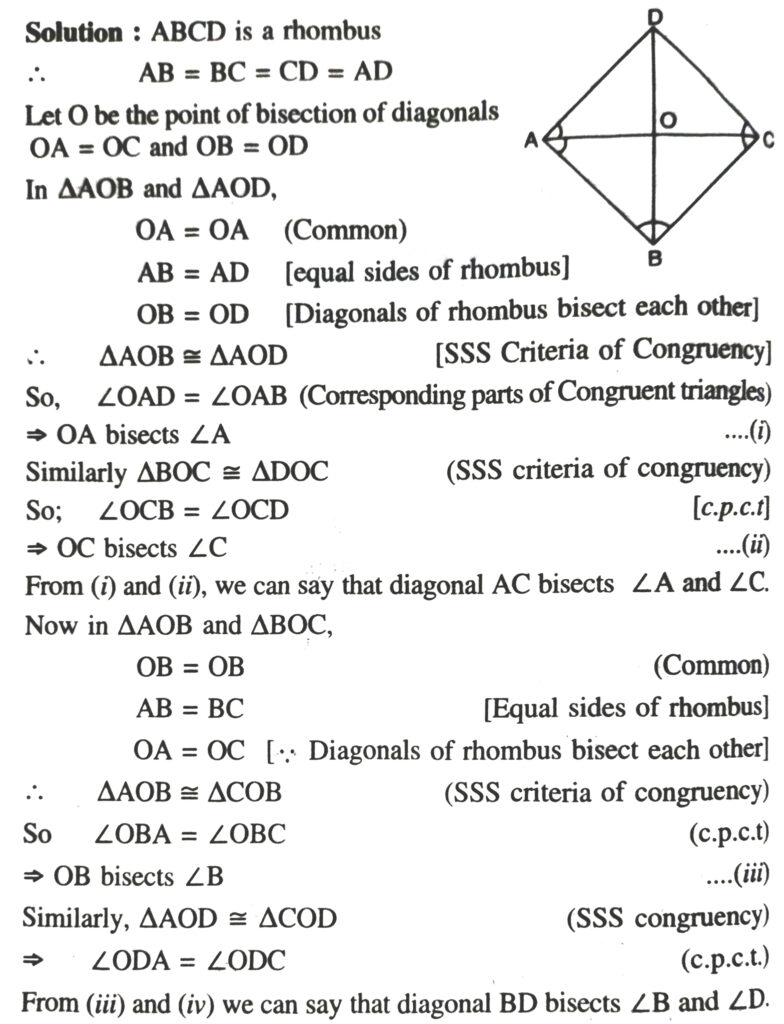
6. Diagonal AC of a parallelogram ABCD bisects ∠A (See fig.). Show that

(i) It bisects ∠C also

(ii) ABCD is a rhombus.

7. ABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

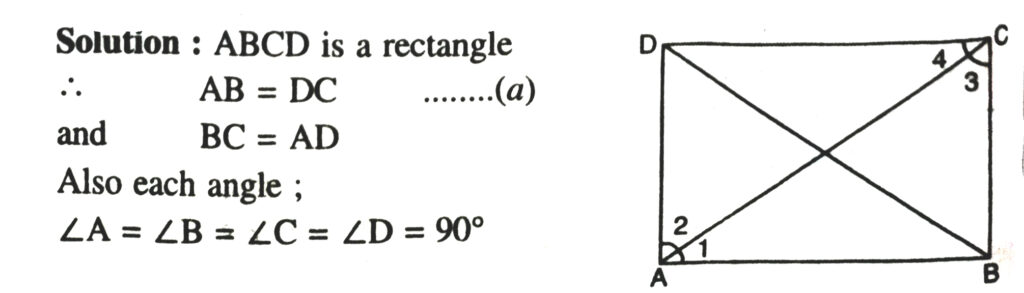
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) Diagonal BD bisects both ∠B as well as ∠D.

9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.). Show that

(i) ΔAPD ≅ ΔCQB

(ii) AP = CQ

(iii) ΔAQB ≅ ΔCPD

(iv) AQ = CP

(v) APCQ is a parallelogram.

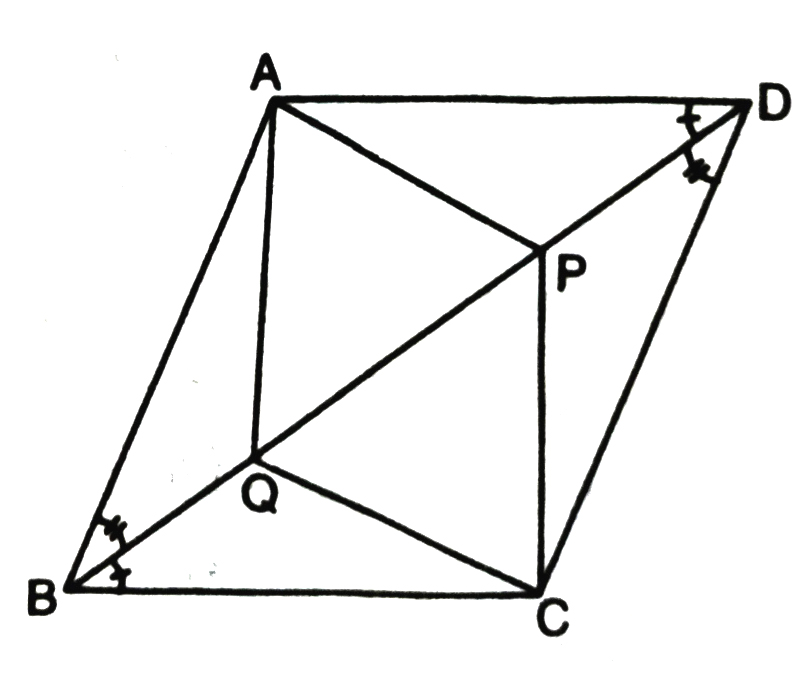
Opposite P Opposite sides of quadrilateral APCQ are equal.

As we know that in a parallelogram opposite sides are equal.

Hence APCQ is a parallelogram.

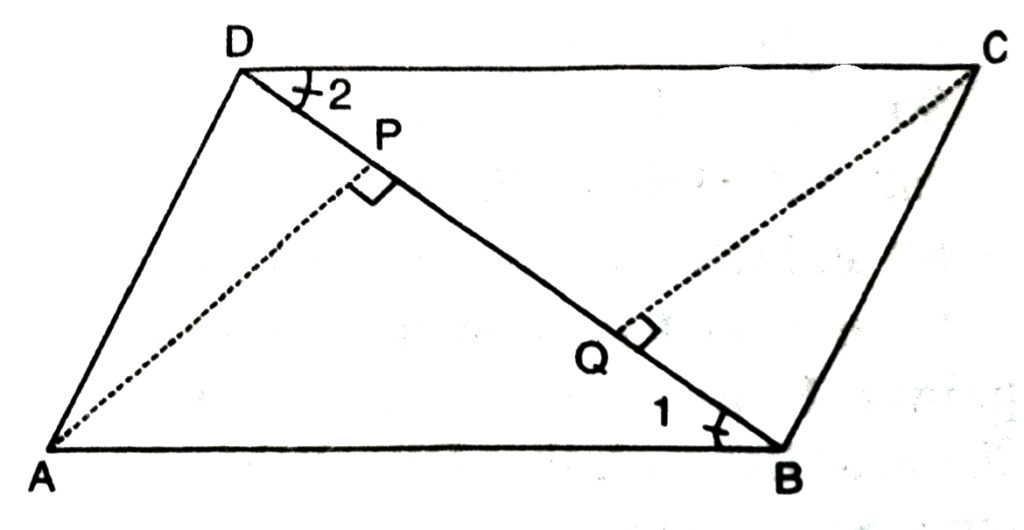
10. ABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its diagonal BD (See fig.) Show that

(i) ΔΑΡΒ ≅ ΔCOD

(ii) AP = CQ

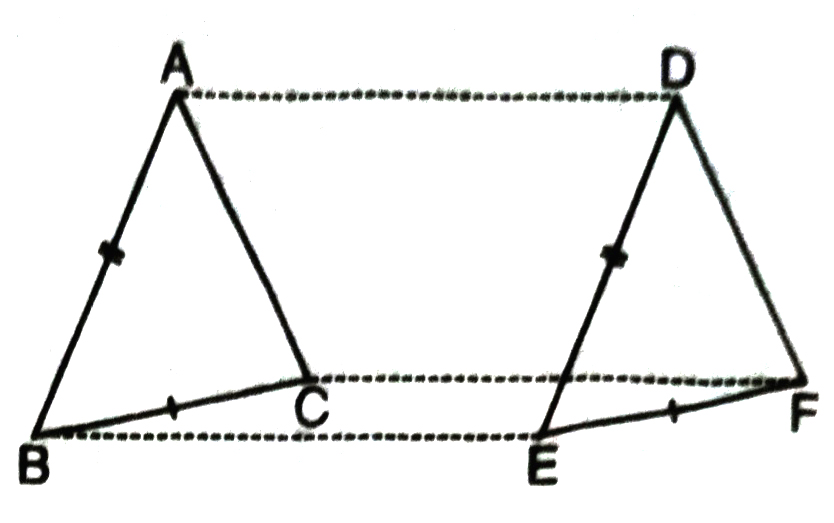
11. In ΔABC and ΔDEF; AB = DE, AB ΙΙ DE, BC = EF and BC ΙΙ EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.). Show that

(i) quadrilateral ABED is a parallelogram

(ii) quadrilateral BEFC is parallelogram

(iii) AD ΙΙ CF and AD = CF

(iv) Quadrilateral ACFD is a parallelogram.

(v) AC = DF

(vì) ΔABC ≅ ΔDEF

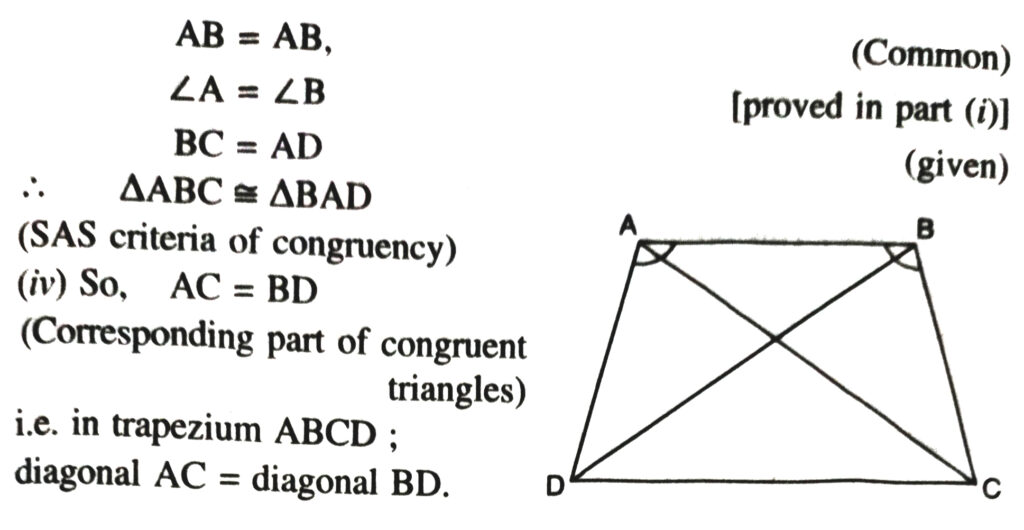
12. ABCD is a trapezium in which AB ΙΙ CD and AD = BC (See Fig.) Show that

(i) ∠A = ∠B

(ii) ∠C = ∠D

(iii) ΔABC ≅ ΔBAD

(iv) diagonal AC = diagonal BD.

MID-POINT THEOREM

Theorem 12. The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

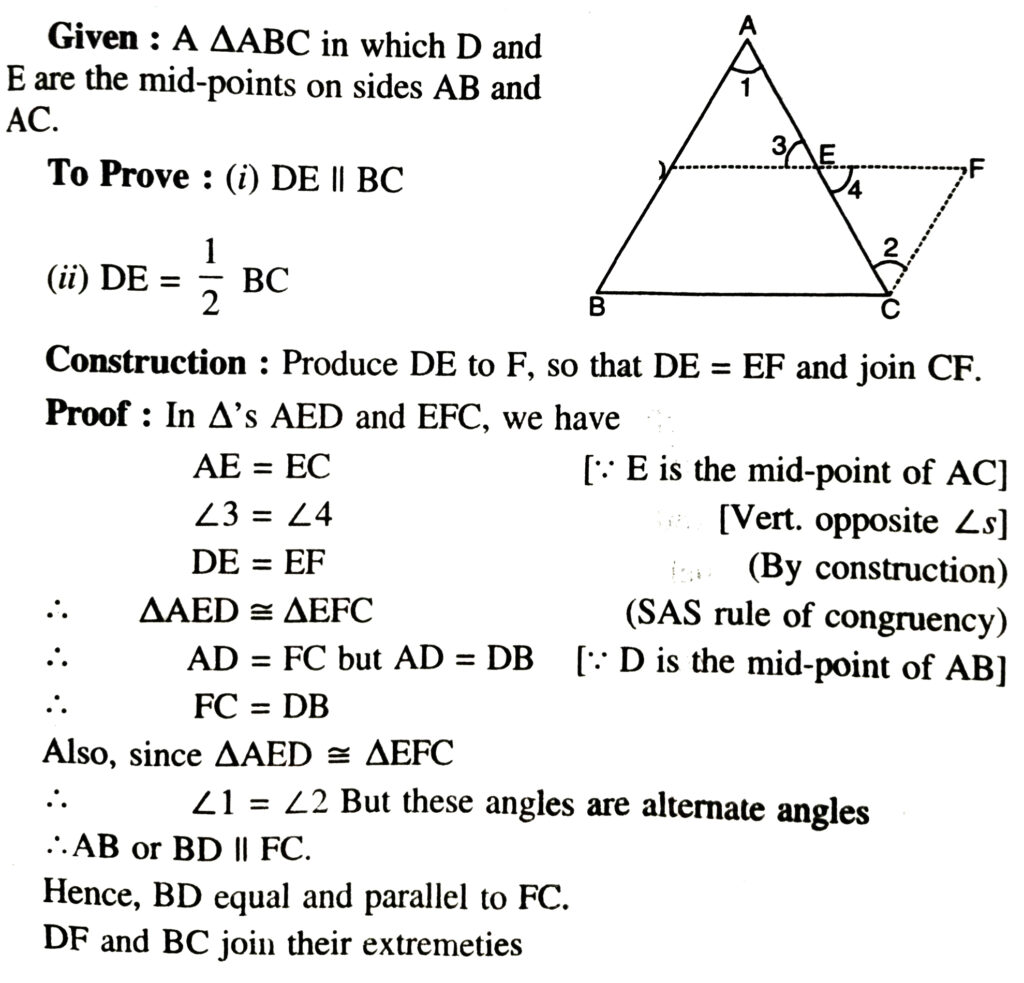
Theorem 13. (Converse of theorem 12) The line drawn through the mid-points of one side of a triangle, parallel to another side, intersects the third side at its mid-point.

MUST REMEMBER

1. The segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.

2. The line drawn through the mid-points of sides of a triangle is parallel to another side and intersect the third-side at its mid-points.

INTERCEPTS

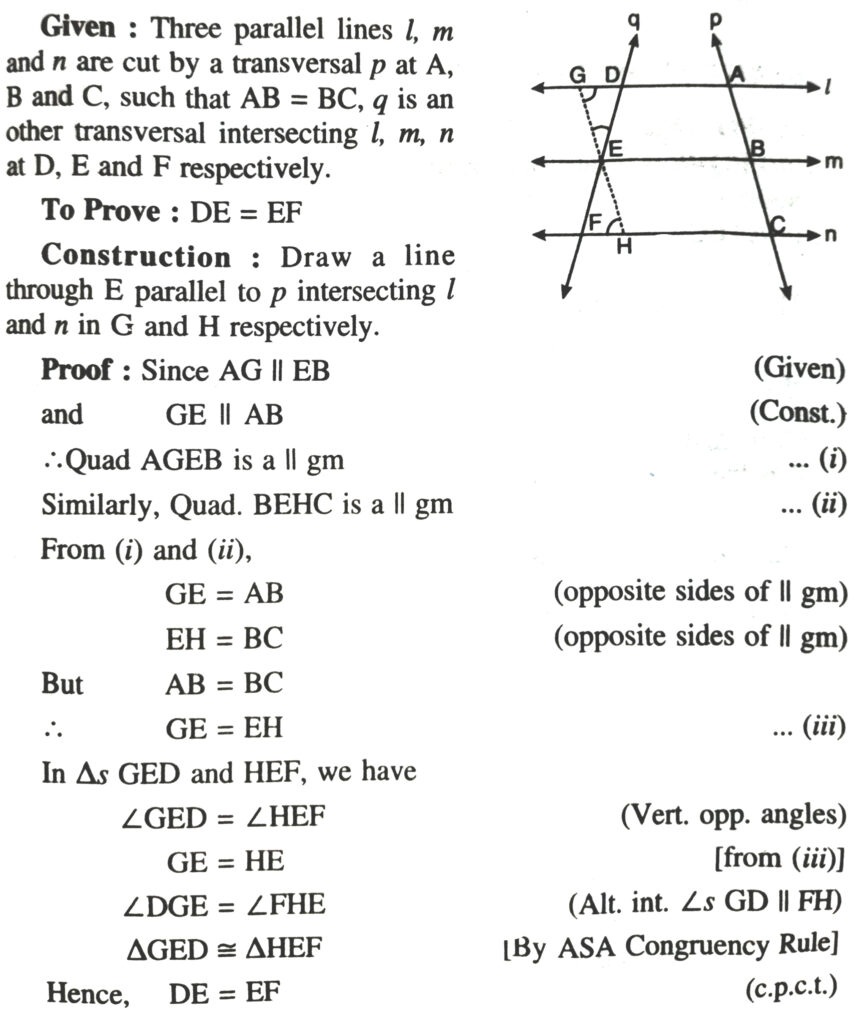
Theorem 14. If there a If there are three parallel lines, and the intercepts made by them on one transversal are equal, then the intercepts on any other transversal are also equal.

MUST REMEMBER

If there are three parallel lines and the intercepts made by them on one transversal are equal, then the intercepts on any other transversal are also equal.

TEXT BOOK EXERCISE – 8.2

1. ABCD is a quadrilateral in which P, Q, R and S are the midpoints of sides AB, BC, CD and DA respectively (See Fig.) AC is a diagonal. Show that

(i) SR II AC and SR =1/2 AC

(ii) PQ = SR

(iii) PQRS is a parallelogram.

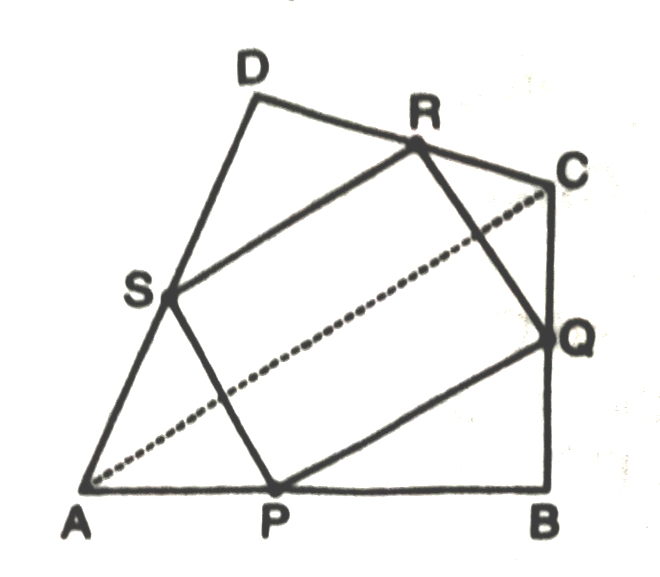
As we know that if one pair of opposite sides of a quadrilateral is equal and parallel then it is a parallelogram.

∴ PQRS is a parallelogram.

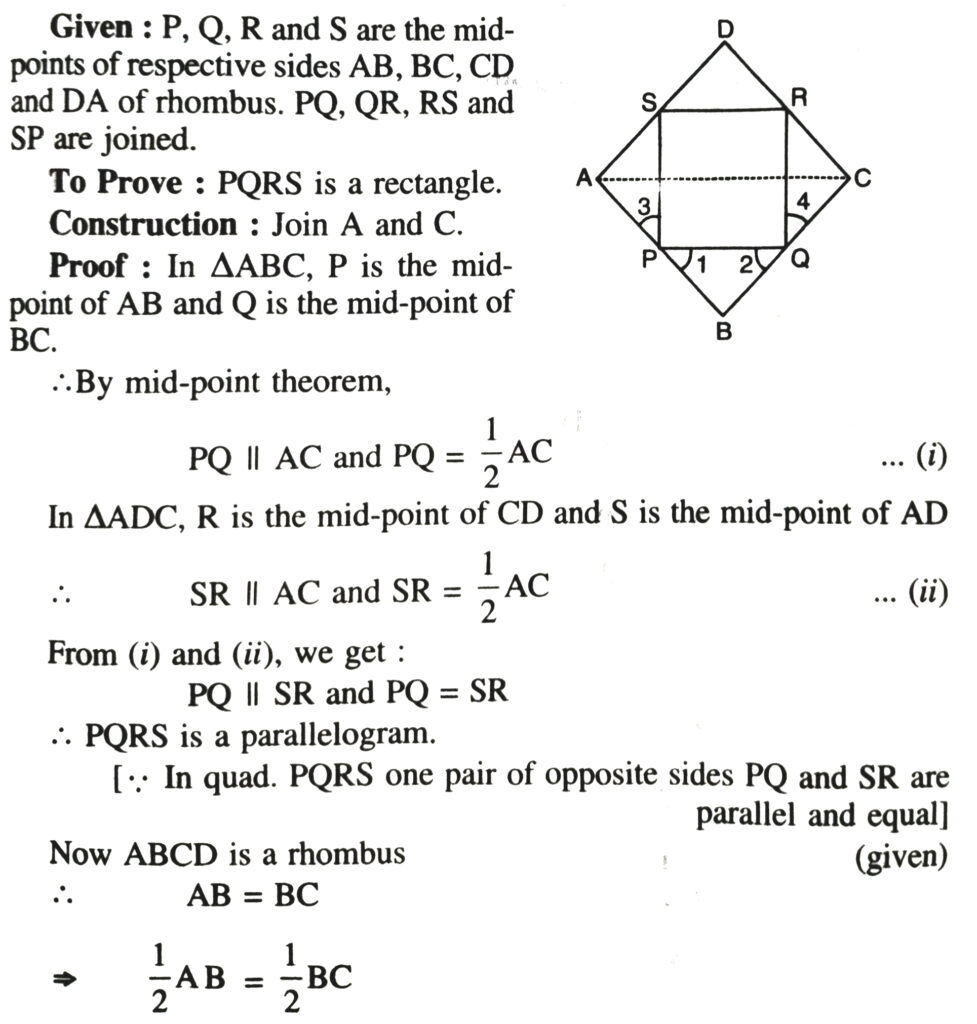
2. ABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.

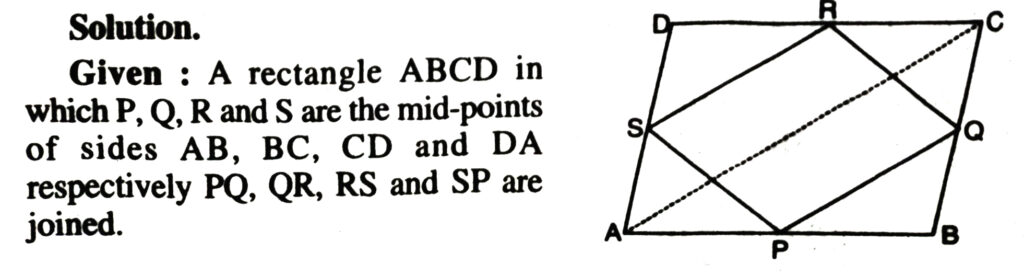
3. ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

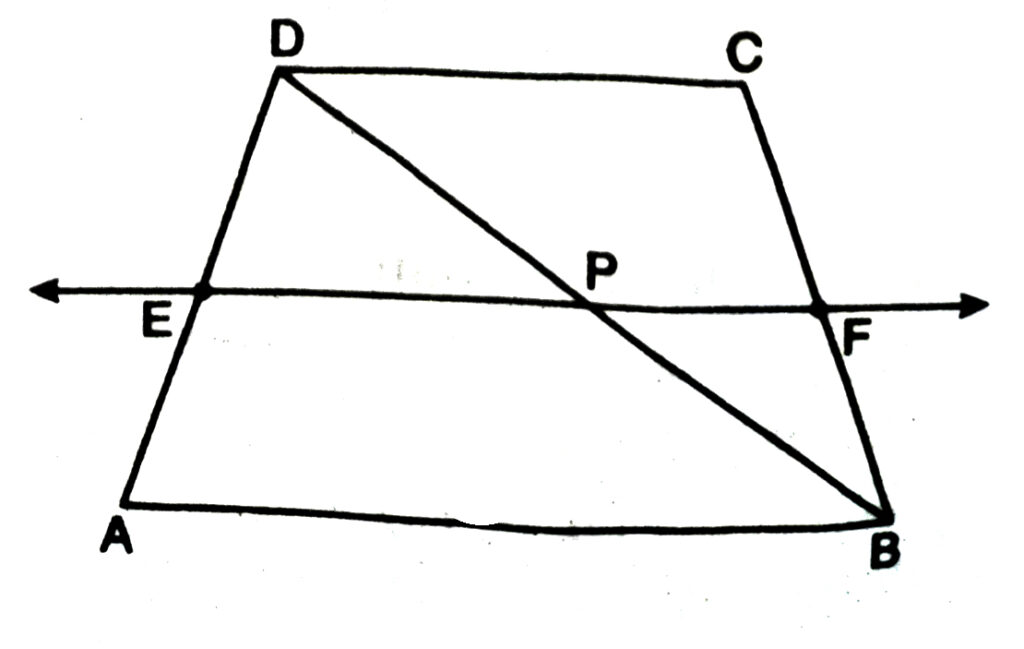
4. ABCD is a trapezium, in which ABΙΙ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E, parallel to AB intersecting BC at F (See Fig.). Show that F is the mid-point of BC.

5. In a parallelogram ABCD, E and F are the mind-points of sides AB and CD respectively (See Fig). Show that the line segments AF and EC trisect the diagonal BD.

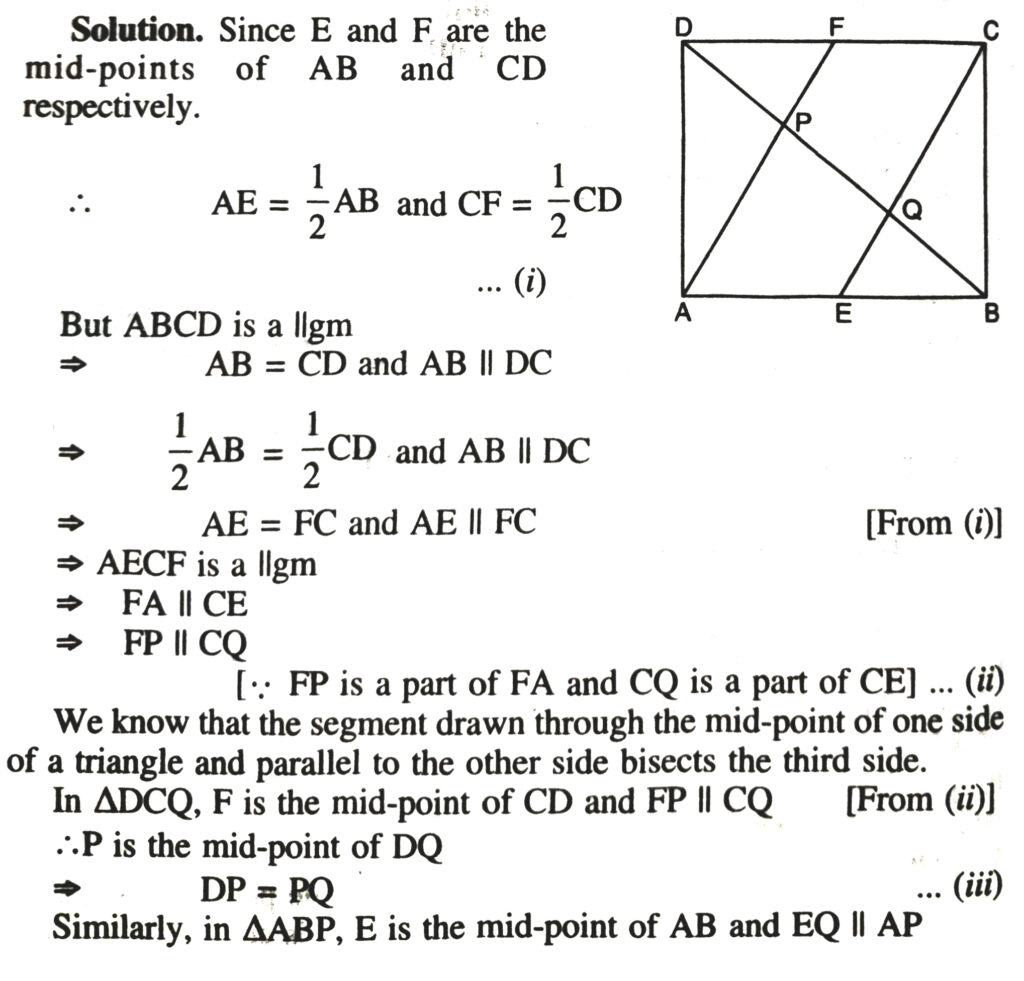
6. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.

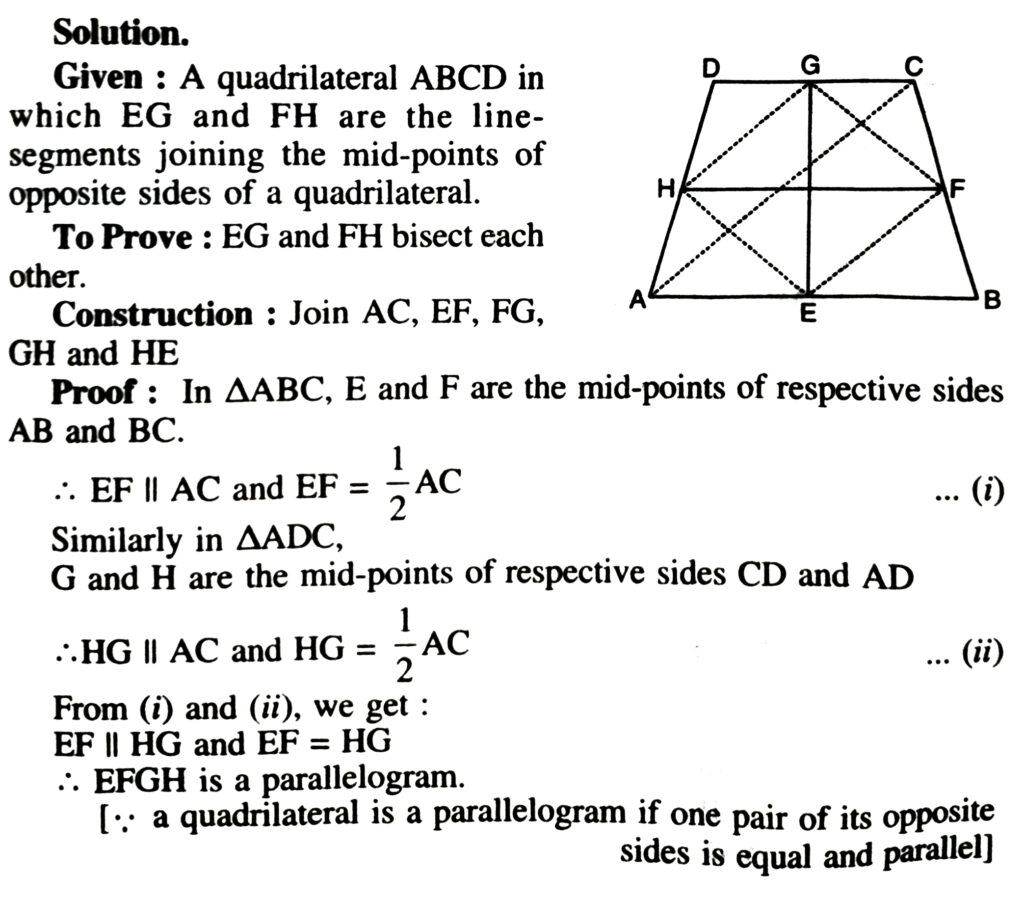
As we know, that the diagonals of a parallelogram bisect each other therefore line segments (i.e. diagonals) EG and FH (of parallelogram EFGH) bisect each other.

7. ABC is a triangle right angled at C. A line through the mid. point M of hypotenuse AB and parallel to BC intersects AC at D.

Show that :

(i) D is the mid-point of AC

(ii) MD ⊥ AC

(iii) CM = MA = 1/2 AB.

WNA24

JKBOSE 9th Class Mathematics Solutions Chapter 8 Quadrilaterals