JKBOSE 9th Class Mathematics Solutions Chapter 9 Areas Of Parallelograms And Triangles

03/26/202303/26/2023 keshav kumar 77 Views 0 Comments

Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions

J&K class 9th Mathematics Areas Of Parallelograms And Triangles Textbook Questions and Answers

INTRODUCTION

In the previous classes we had studied that part of the plane enclosed by a simple closed figure is called a planar region corresponding to the figure. The magnitude or measure of this planar region is called its area. This magnitude or measure is always expressed with the help of a number (in some unit) such as 5 cm², 8 m²2 etc. So, we can say that area of a figure is a number (in some unit) associated with the part of the plane enclosed by the figure.

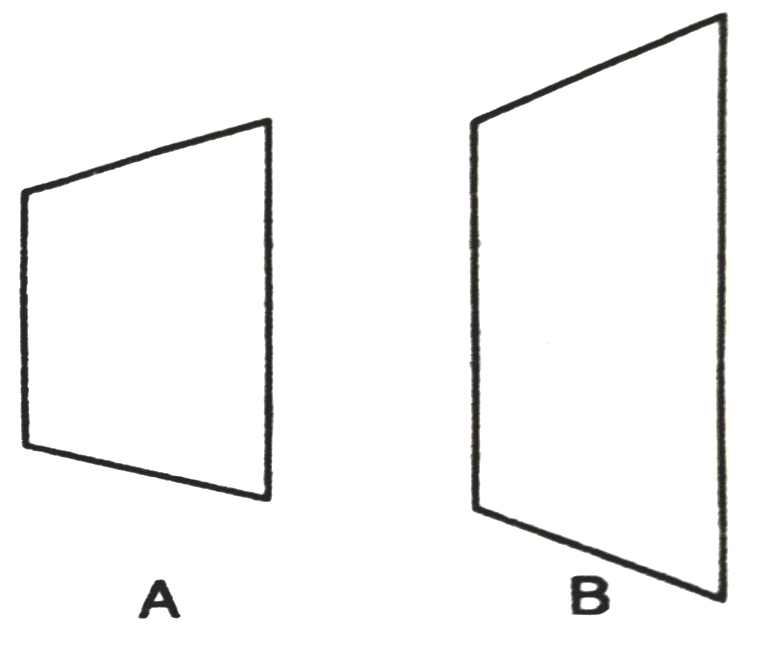
We are also familiar with the concept of congruent figures from earlier classes and from Chapter 7. Two figures are called congruent, if they have the same shape and the same size. In other words, if two figures A and B are congruent (See Fig.), then using a tracing paper, we can superpose one figure over the other.

So, if two figures A and B are congruent, they must have equal areas but two figures having equal areas need not be congruent.

In earlier classes, you have learnt about some formulae for finding the areas of different figures such as rectangle, square, parallelogram, triangle etc. In this chapter, attempt shall be made to consolidate the knowledge about these formulae by studying some relationship between the areas of these geometric figures under the condition when they lie on the same base and between the same parallels. This study will also be useful in the understanding of some results in the next class.

AREAS OF POLYGONS ON THE SAME BASE AND BETWEEN THE SAME PARALLELS

If two or more polygons (triangles, parallelograms etc.) are drawn so that their bases lie on a line CD and vertices on another line AB, and AB II CD, then these polygons are said to be on the same base and between the same parallels AB and CD.

Polygons between the same parallels have equal altitudes.

TEXT BOOK EXERCISE – 9.1

1. Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

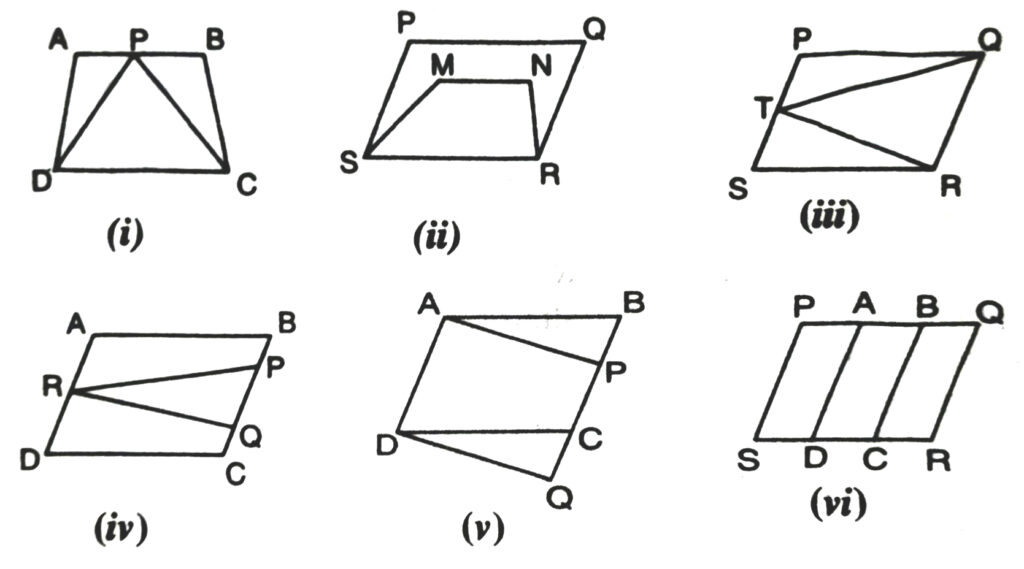
Solution.— In Fig. (i); ΔDPC and trap. ABCD are on the same base DC and between same parallels DC and AB.

In Fig. (iii); ΔRTQ and parallelogram PQRS are on the same oll base QR and between same parallel QR and PS.

In Fig. (v); Parallelogram ABCD and parallelogram APQD are on the same base AD and between the same parallels AD and BQ.

APPLICATION OF CONGRUENT AREA AXIOM

1. AREA OF A PARALLELOGRAM

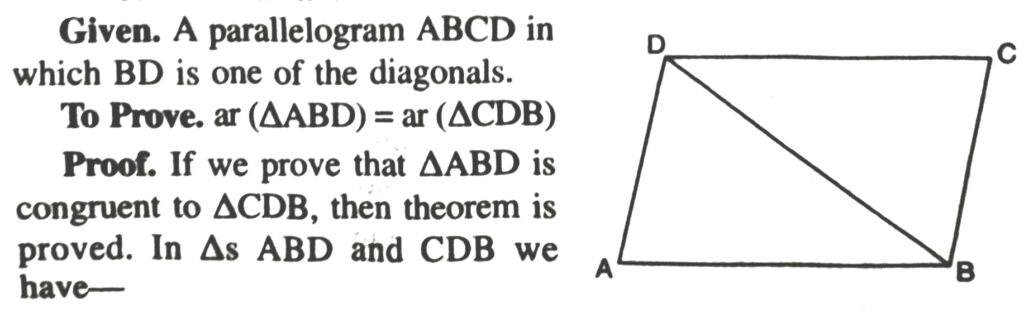
Theorem 1. A diagonal of parallelogram divides it into two triangles of equal area.

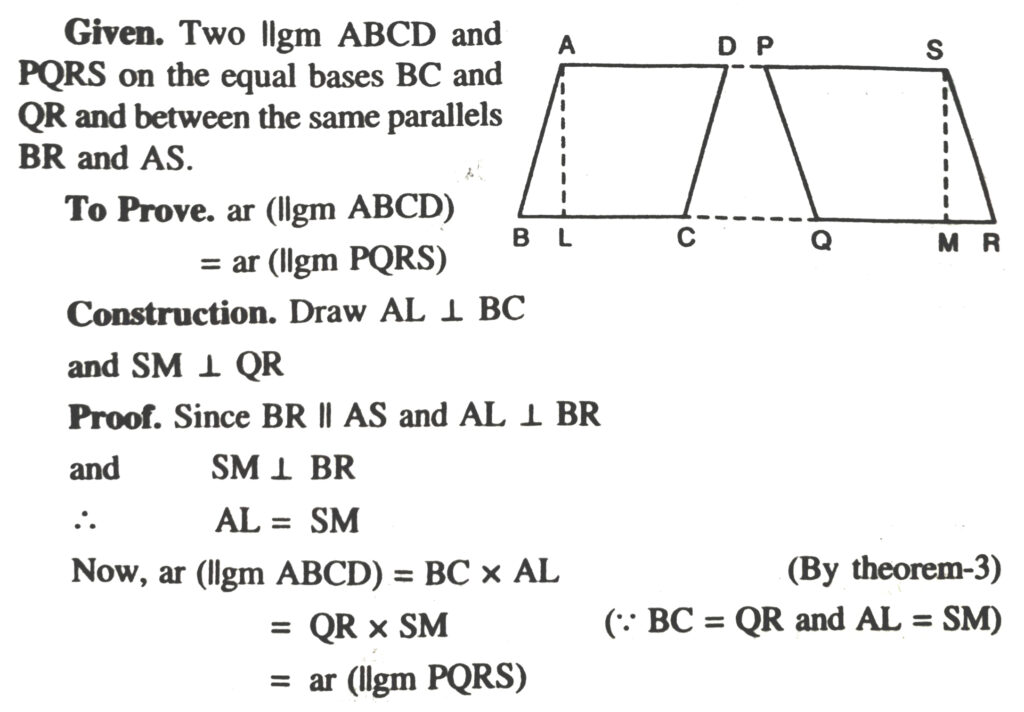
Theorem 2. Parallelogram on the same base and between the same parallels (i.e. of equal altitude) are equal in area.

Corollary-The area of a parallelogram is equal to the area of a rectangle on the same base and of the same altitude.

Proof. Since rectangle is also a parallelogram, proof of this corollary follows from the proof of theorem-2.

Theorem 3. The area of a parallelogram is the product of its base and the corresponding altitude.

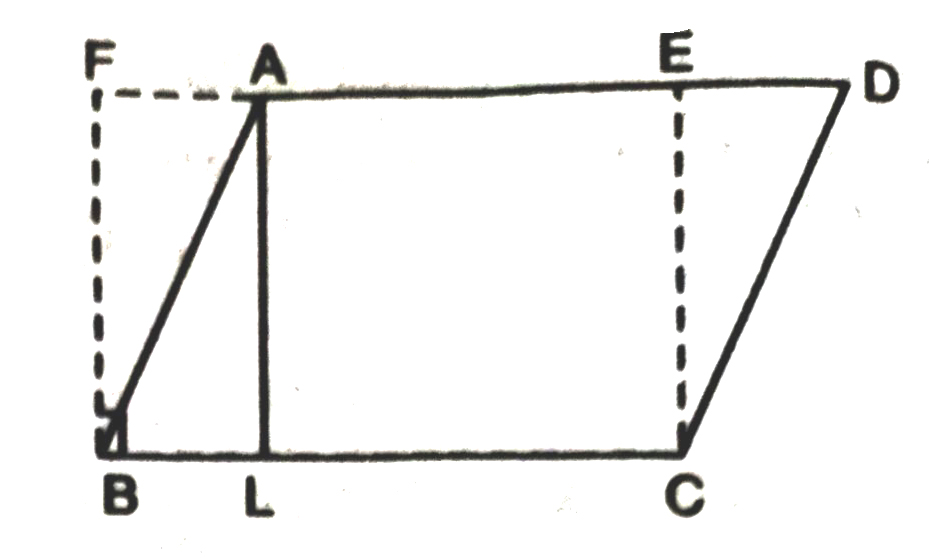
Corollary 1. Parallelogram on equal bases and between the same parallels are equal in area.

Corollary 2. The area of a triangle is half the product of any of its sides and the corresponding altitude.

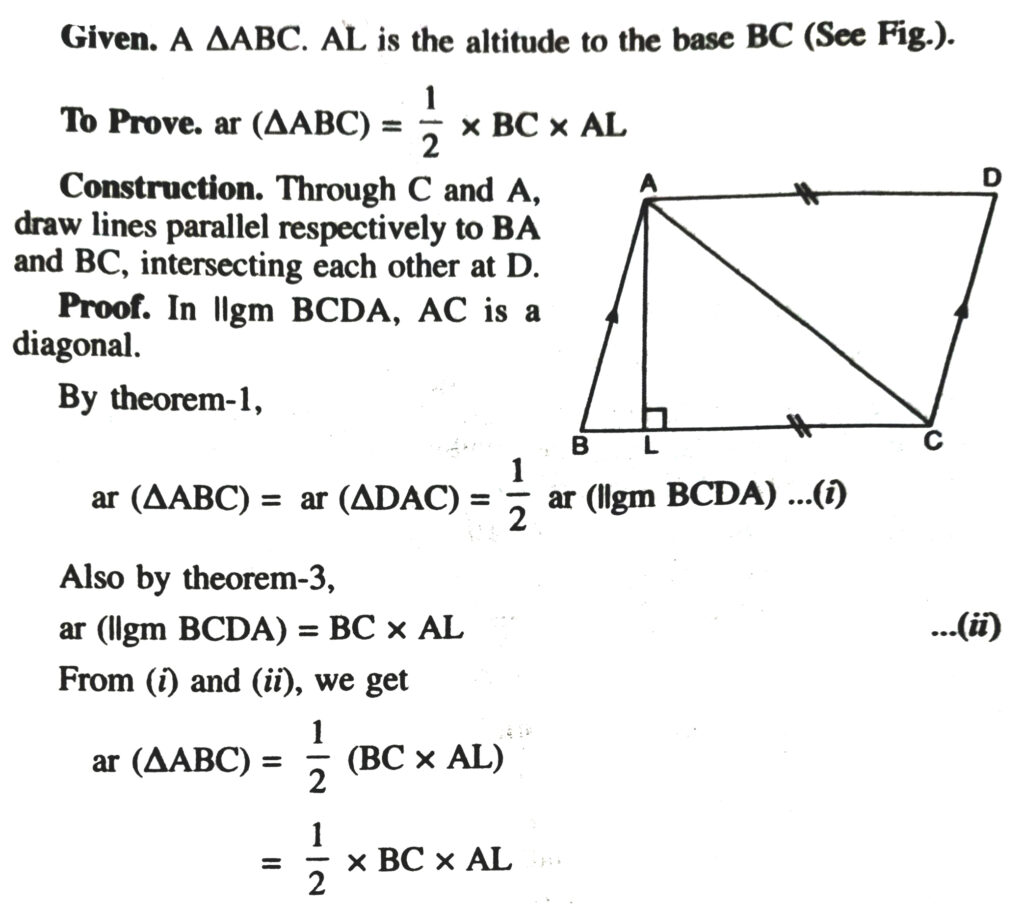
AREA OF A TRIANGLE

Theorem 4. Triangles on the same base and between the same parallels have equal area.

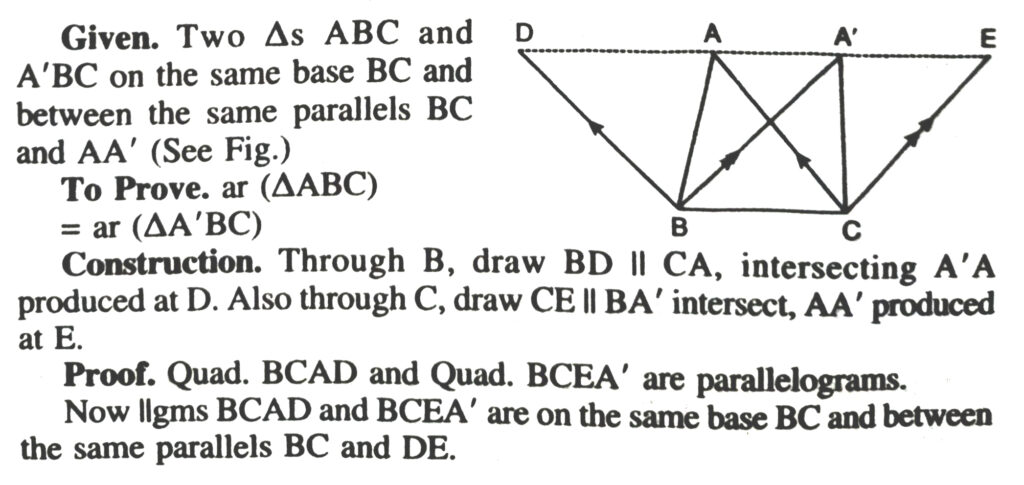
Corollary 1. If a triangle and parallel ogram are on the same base and between the same parallels, the area of the triangle is equal to half that of the parallelogram.

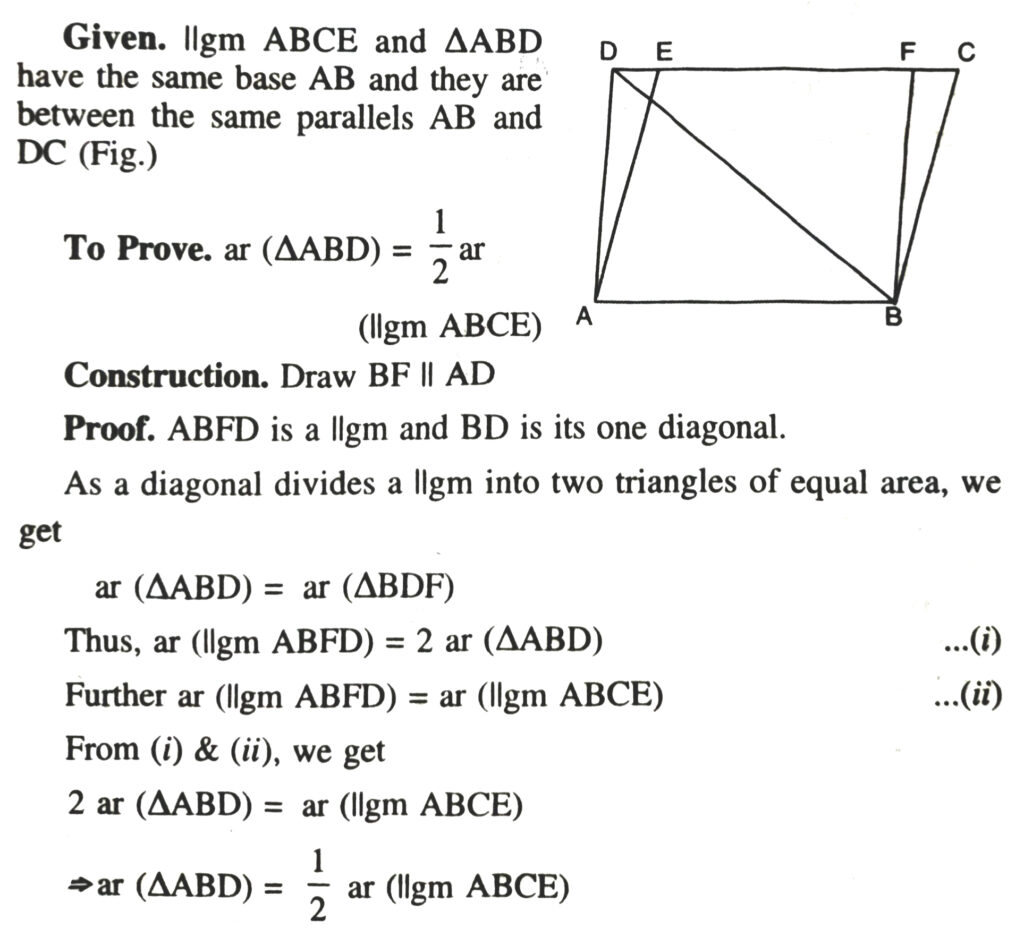
Corollary 2. The area of a trapezium is half the product of its height and the sum of the parallel sides.

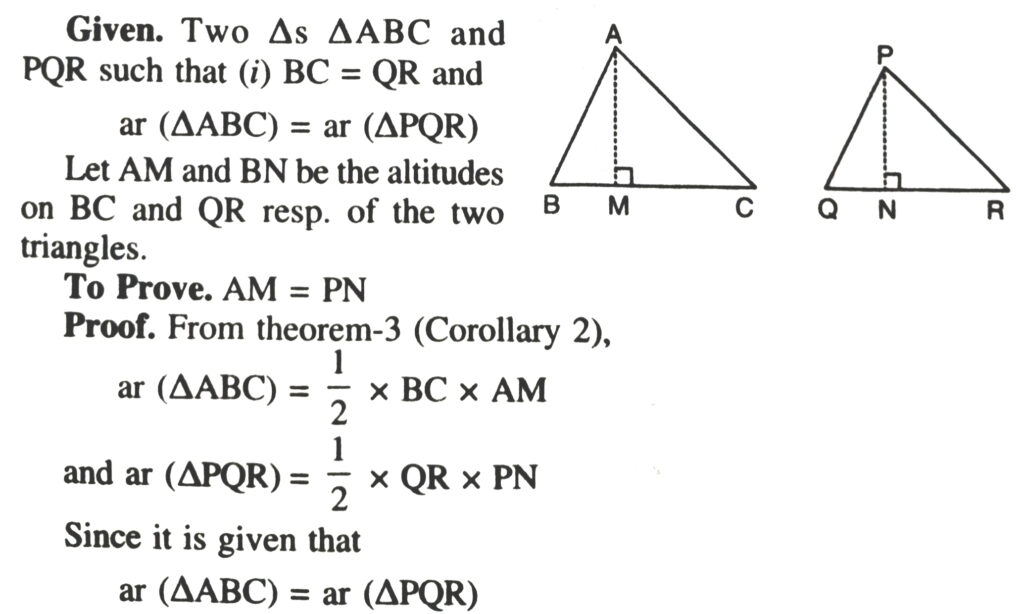
Theorem 5. Triangles having equal areas and having a side of one of the triangles equal to a side of the other, have their corresponding altitudes equal.

TEXT BOOK EXERCISE – 9.2

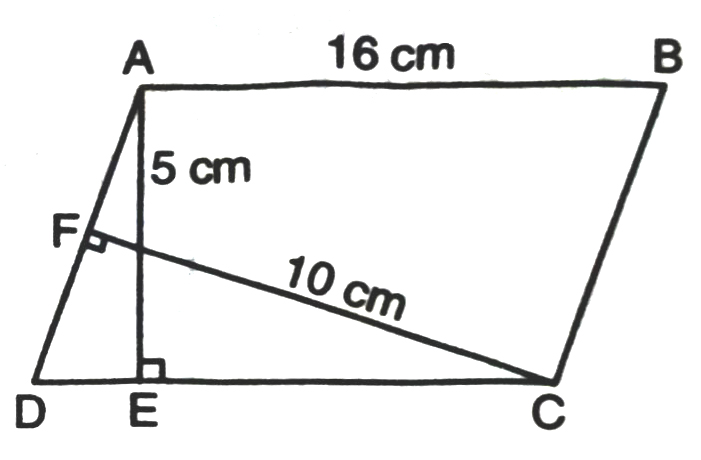
1. In Fig. ABCD is a parallelogram; AE ⊥ DC and HA CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

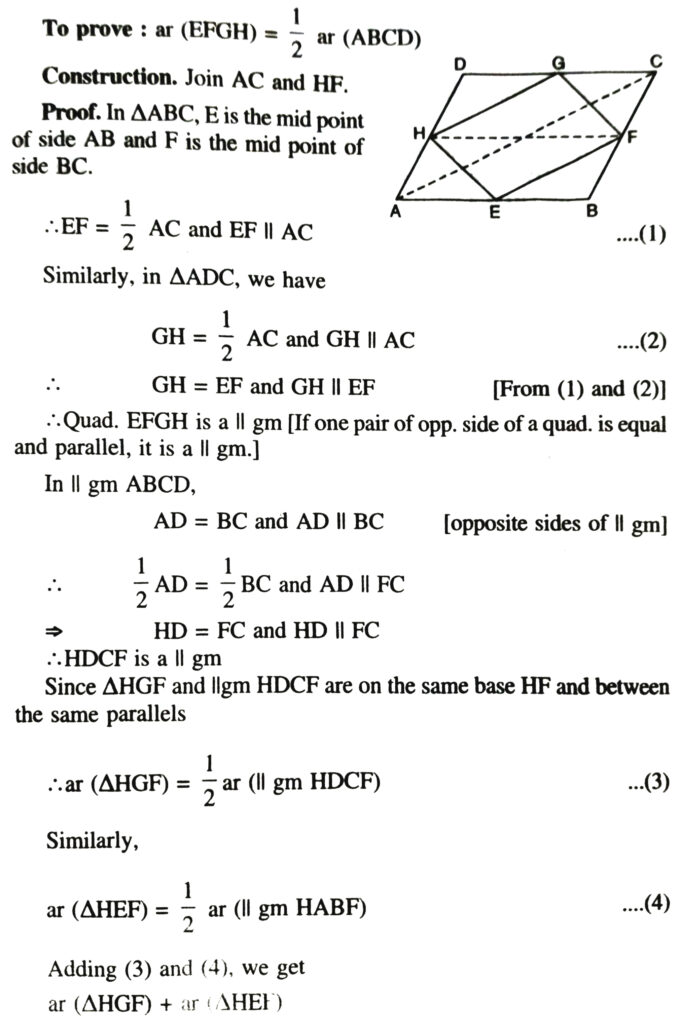
2. If E, F, G and H are respectively the mid-points of the sides this of a parallelogram ABCD, show that ar (EFGH) = 1/2 ar (ABCD).

Solution.— Given that ABCD is a parallelogram. Let E, F, G and H are the mid-points of sides AB, BC, CD and DA respectively.

3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).

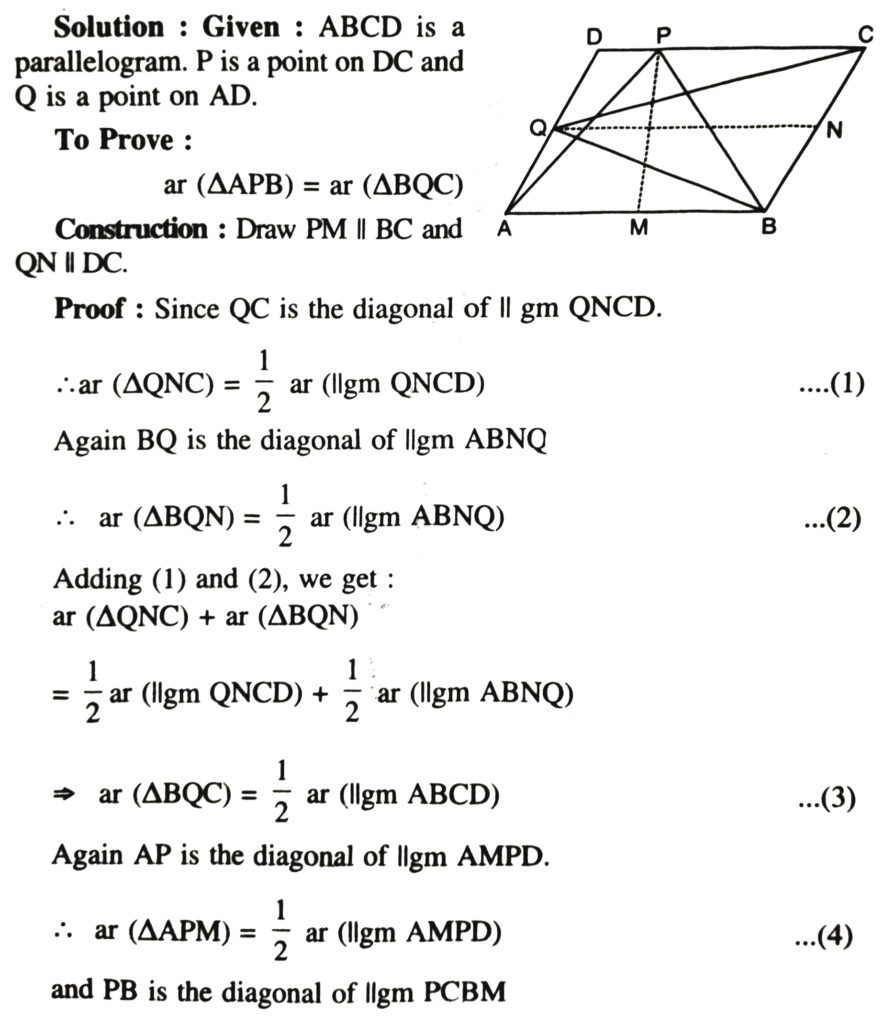
4. In fig. PQRS and ABRS are parallelograms and X is any point on side BR. Show that

(i) ar (PQRS) = ar (ABRS)

(ii) ar (AXS) = 1/2 ar (PQRS)

5. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it ?

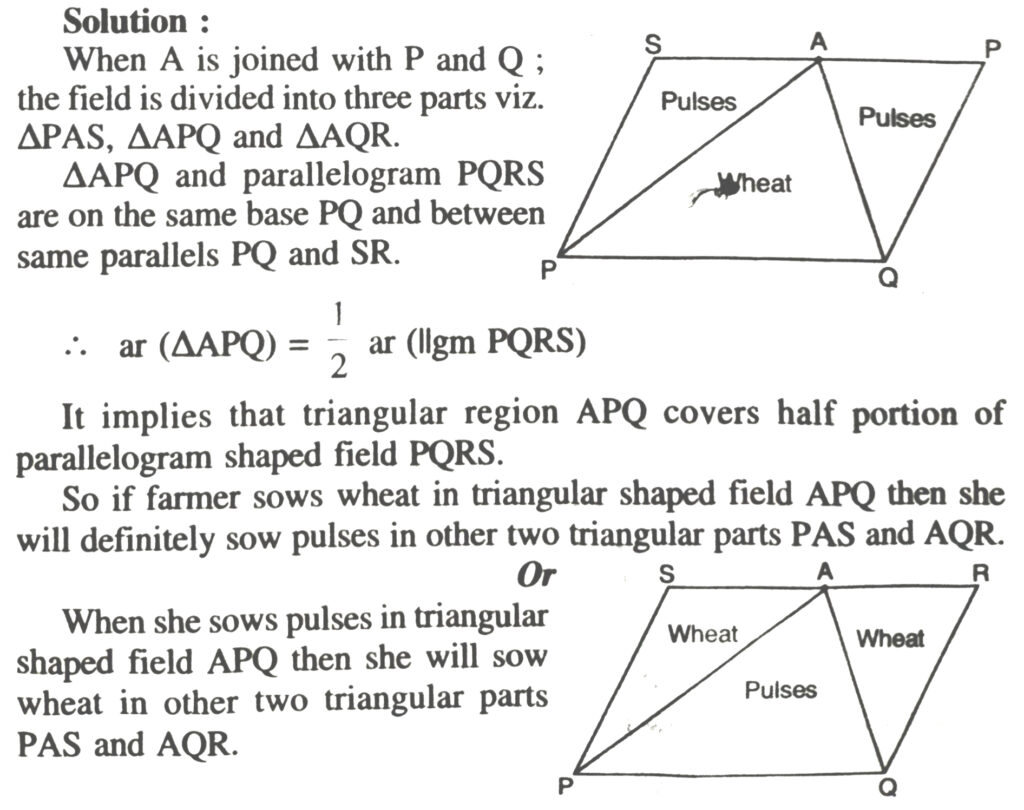
TRIANGLES ON THE SAME BASE AND BETWEEN SAME PARALLELS

In the previous section, we have proved in theorem 4 that two triangles on the same base and between same parallels are equal in area.

Also we have proved in theorem 5 that two triangles with same base (or equal bases) and equal areas will have equal corresponding altitudes.

For having equal corresponding altitudes, the triangles must lie between the same parallels. From this, you arrive at the following converse of Theorem 4.

Theorem 6 : Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.

Let us now take some examples to illustrate the use of the above results.

TEXT BOOK EXERCISE – 9.3

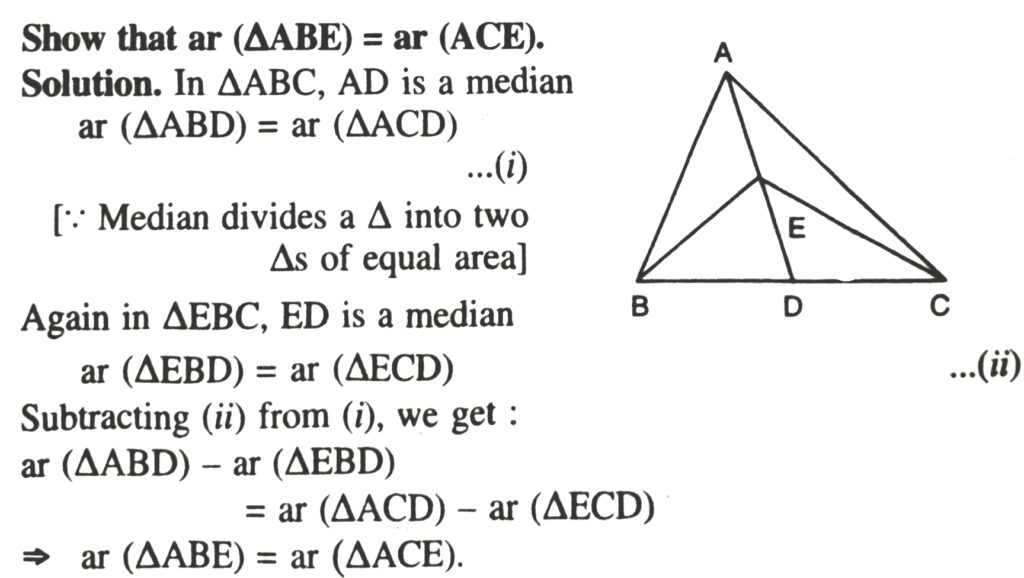
1. In Fig., E is any point on median AD of a ΔABC. Show that ar (ΔABE) = ar (ACE).

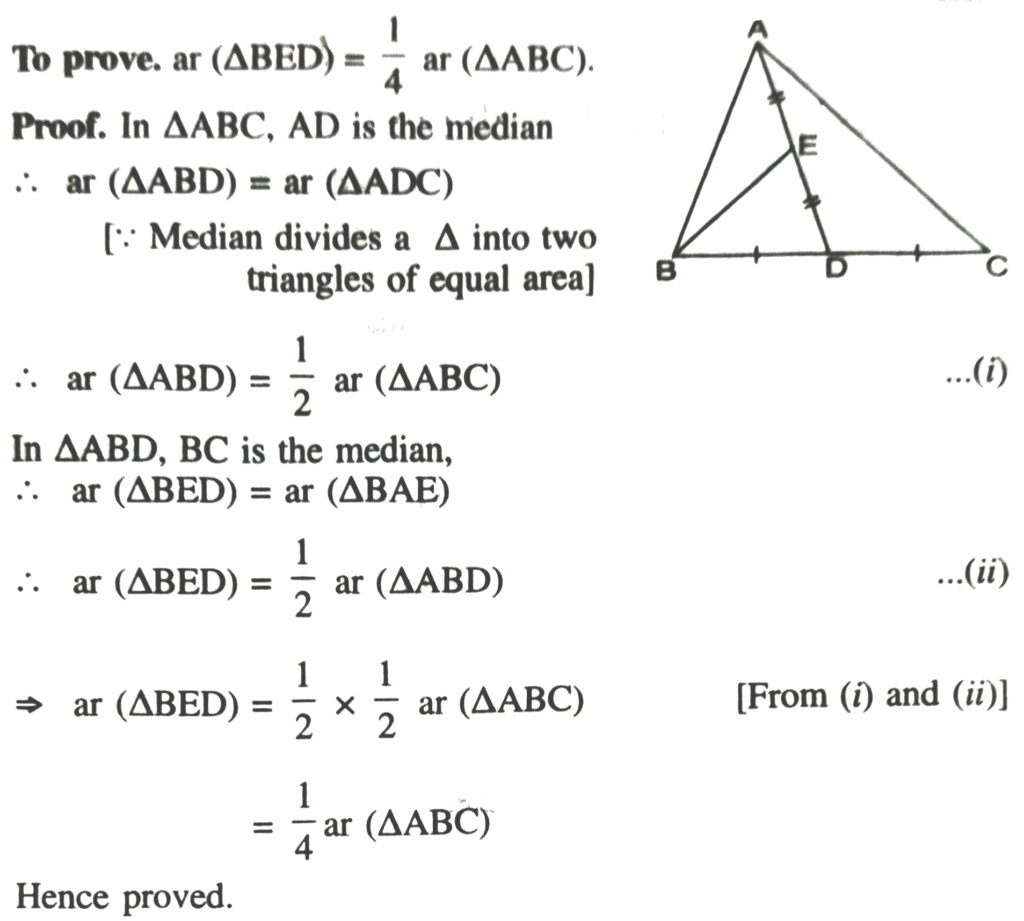
2. In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4 ar (ABC).

Given. A ΔABC, AD is the median and E is the mid-point of median AD.

3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.

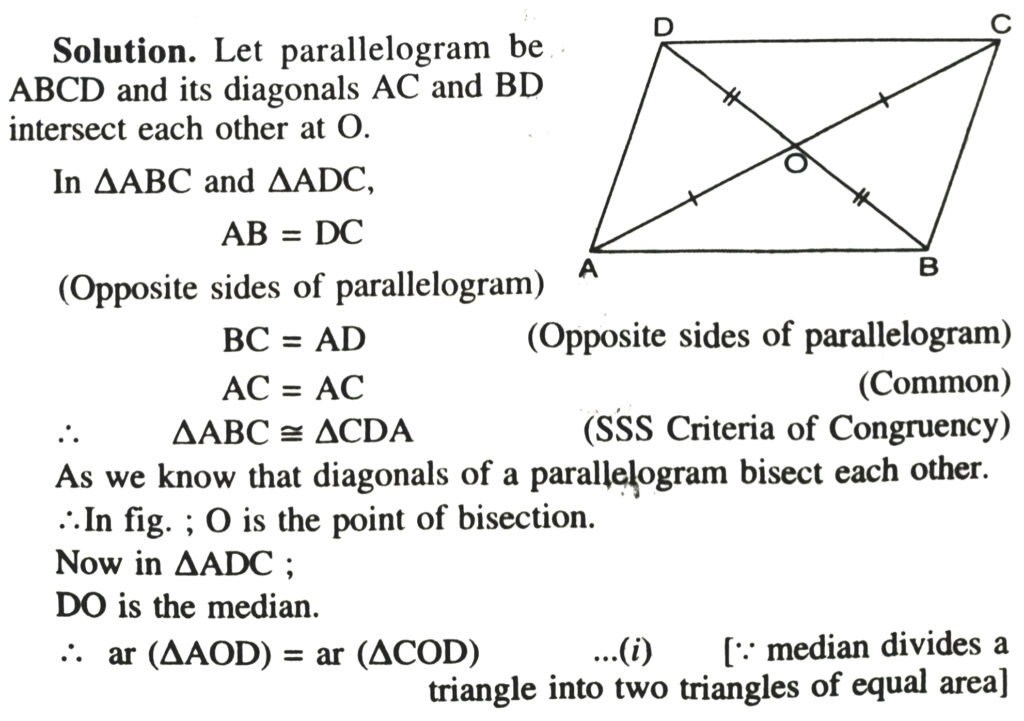
Thus diagonals of parallelogram divide it into four triangles of equal area.

4. In Fig., ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).

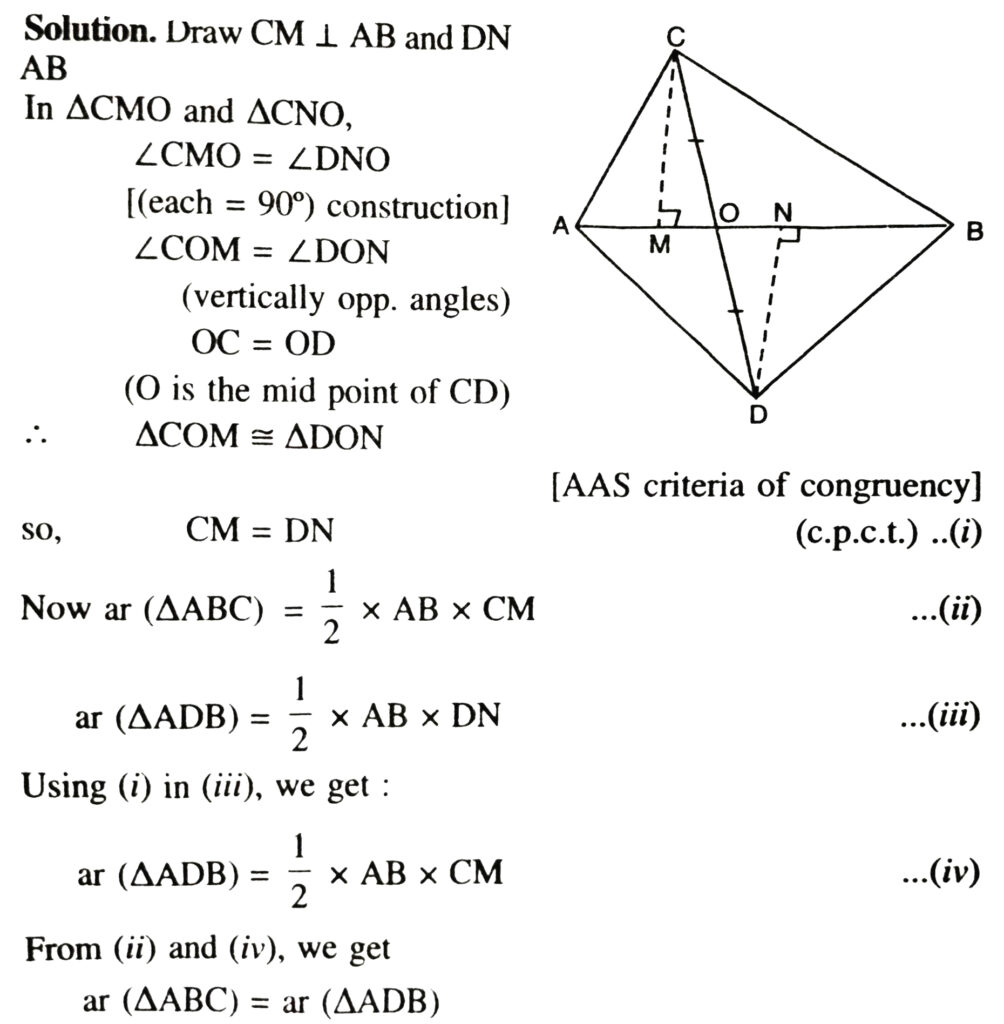
5. D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that

(i) BDEF is a parallelogram.

(ii) ar (DEF) = 1/4 ar (ABC)

(iii) ar (BDEF) = 1/2 ar (ABC).

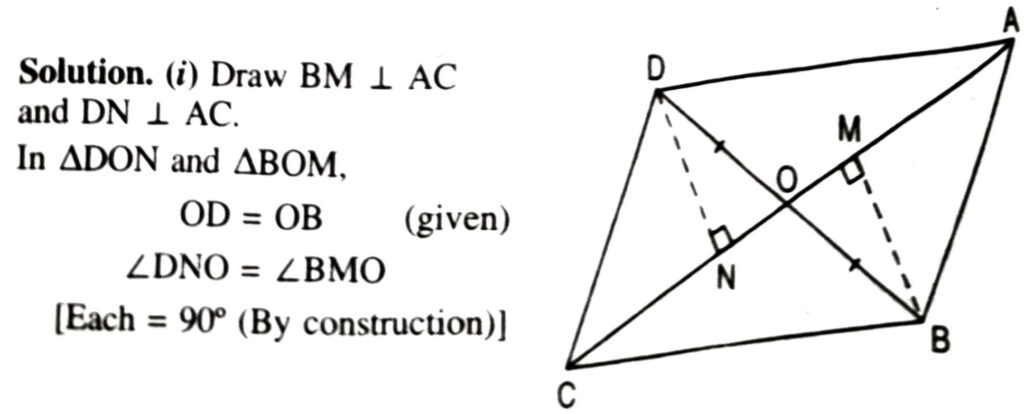
6. In Fig., diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.

If AB = CD, then show that :

(i) ar (DOC) = ar (AOB)

(ii) ar (DCB) = ar (ACB)

(iii) DA ΙΙ CB or ABCD is a parallelogram

7. D and E are points on sides AB and AC respectively of ΔABC such that ar (DBC) = ar (EBC). Prove that DE ΙΙ BC.

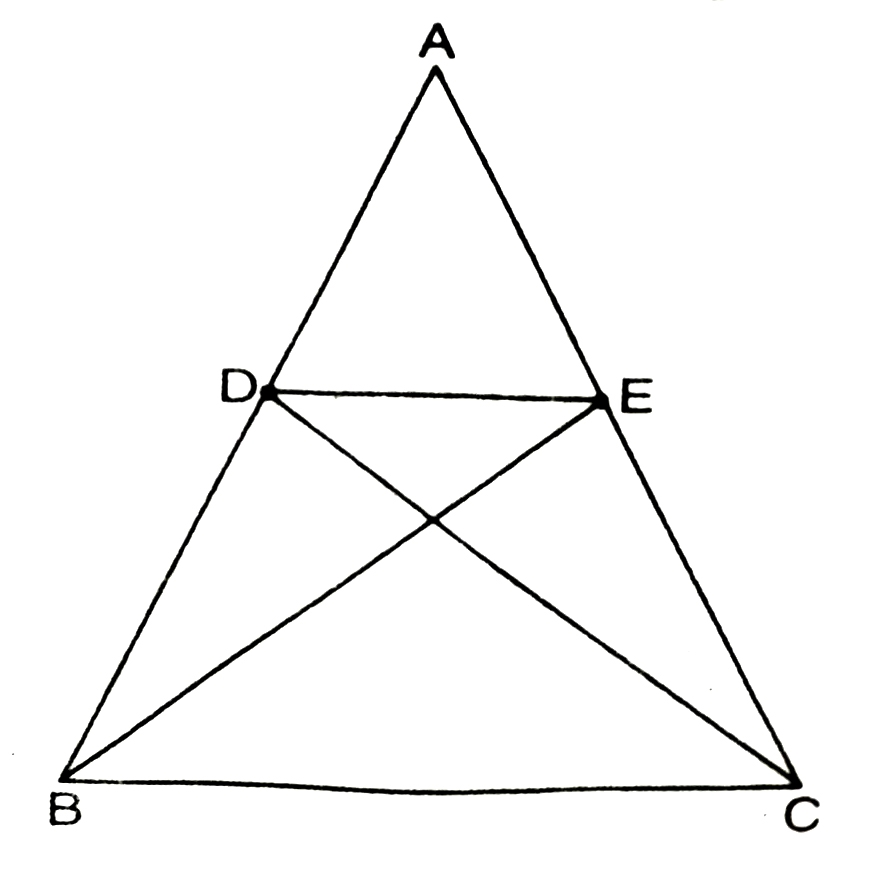
Solution.— Given that ar (ΔDBC) = (ΔEBC)

Two triangles of equal area have common base BC.

Therefore DE ΙΙ BC

[ ∴ Two triangles having same base (or equal bases) and equal areas lie between the same parallels]

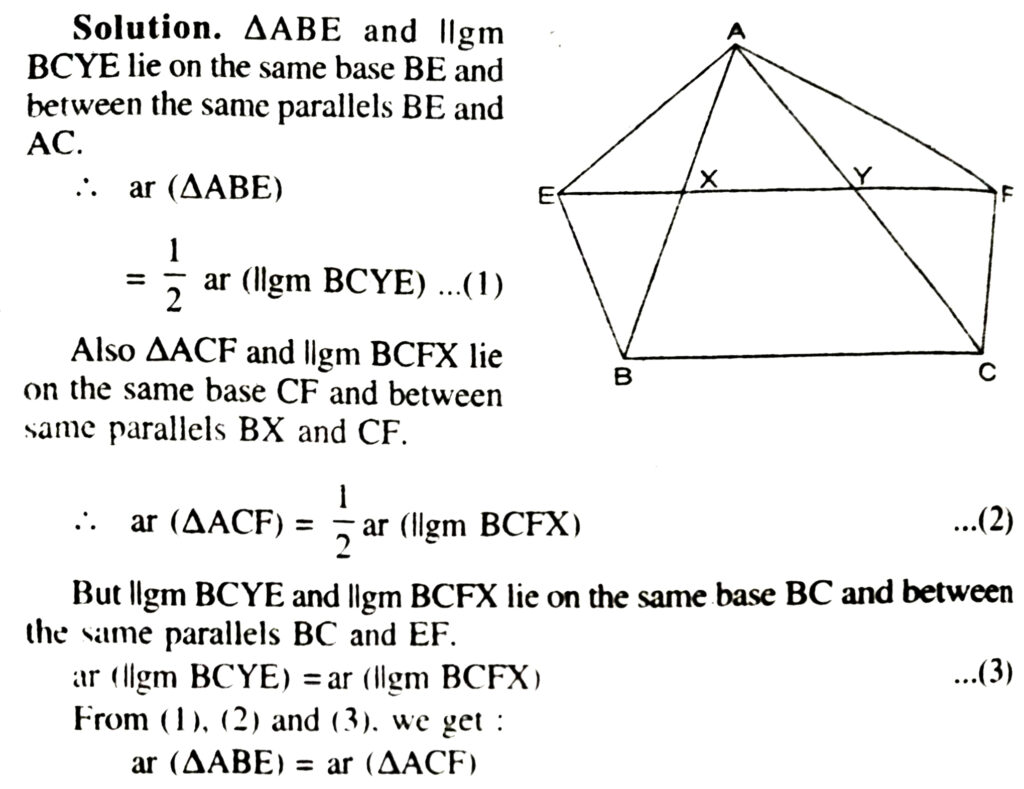
8. XY is a line parallel to side BC of triangle ABC. If BE ΙΙ AC and CF ΙΙ AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).

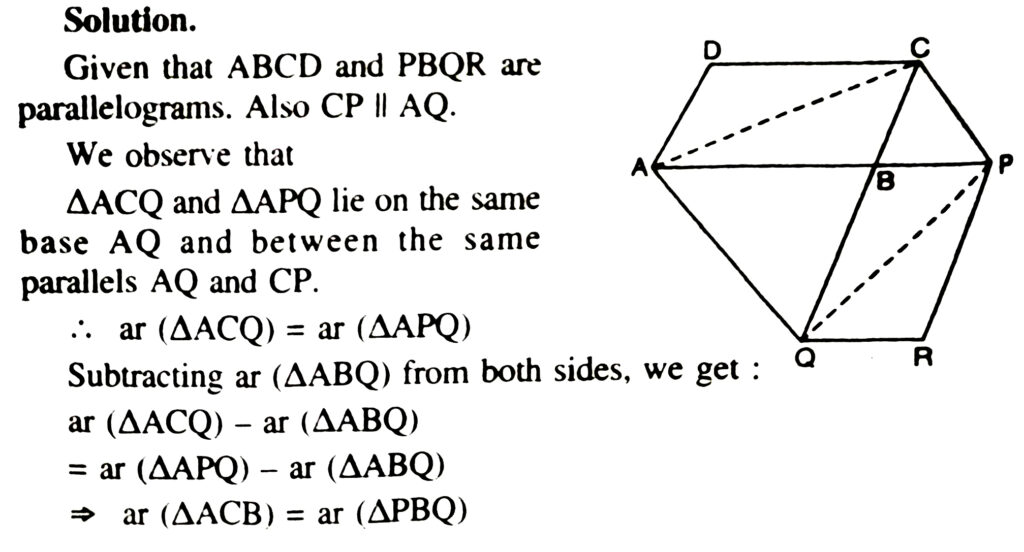
9. The side AB of parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (See Fig.) Show that ar (ABCD) = ar (PBQR).

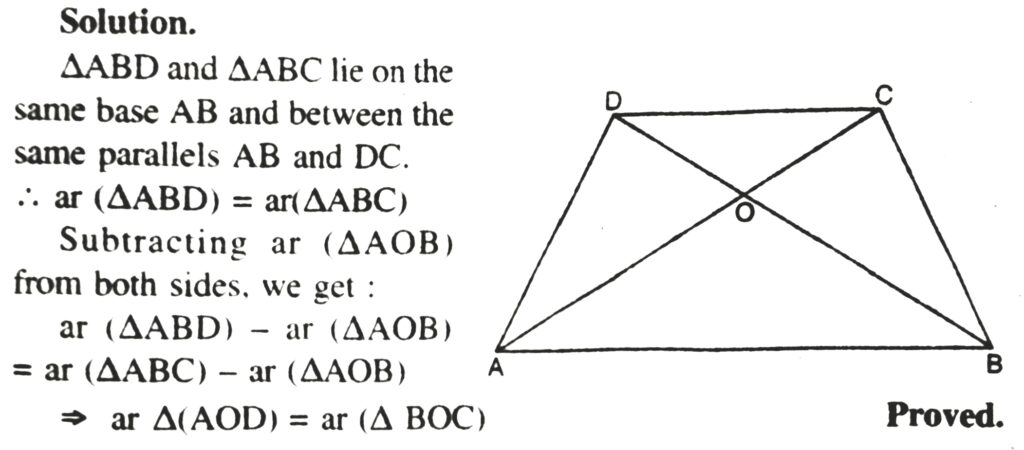
10. Diagonals AC and BD of a trapezium ABCD with AB ΙΙ DC intersect each at O. Prove that ar (AOD) = ar (BOC).

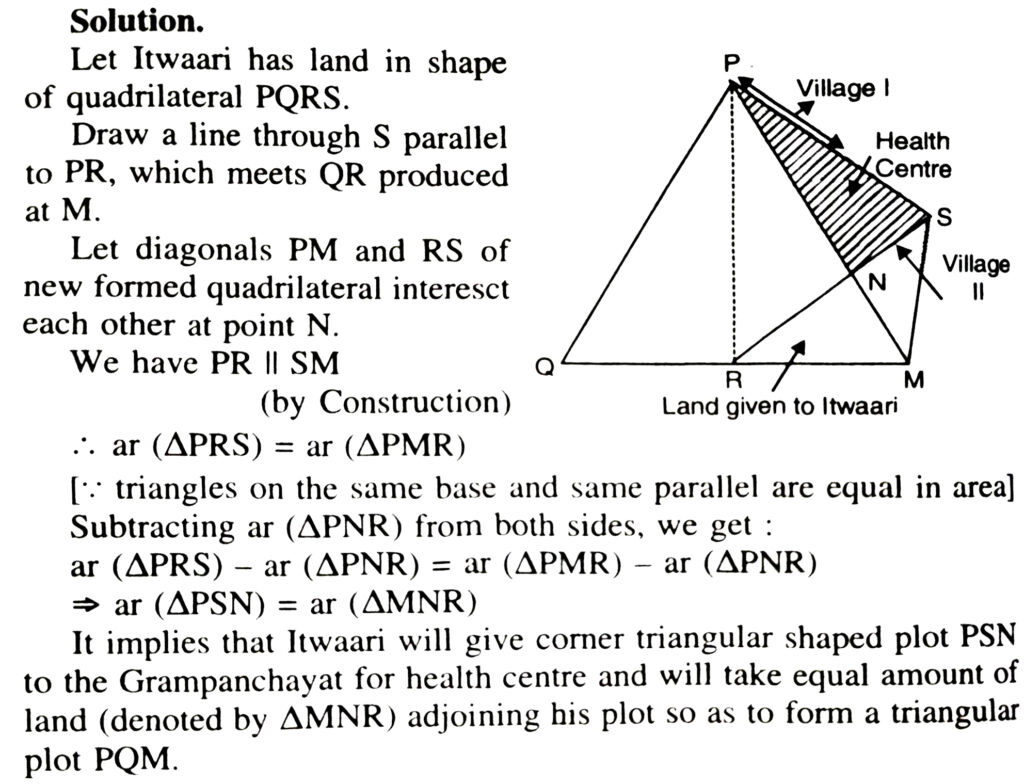
11. A villager Itwaari has a plot of land of the shape of quadrilateral. The Gram Panchayat of two villages decided to take over some portion of his plot from one of the corners to construct a health centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.

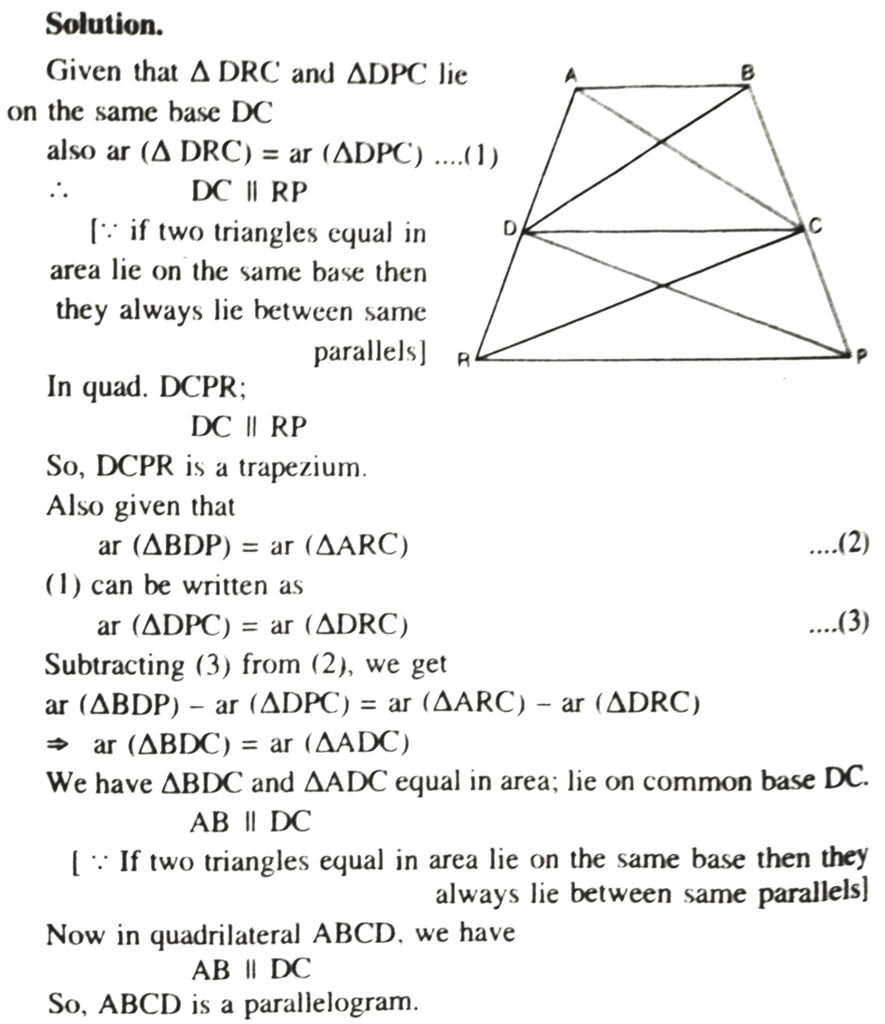
12. In Fig., ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC), Show that both the quadrilaterals ABCD and DCPR are trapeziums.

WNA24

JKBOSE 9th Class Mathematics Solutions Chapter 9 Areas Of Parallelograms And Triangles