PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
PSEB 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
Question 1.
Solve the following pairs of equations by reducing them to a pair of linear equations:
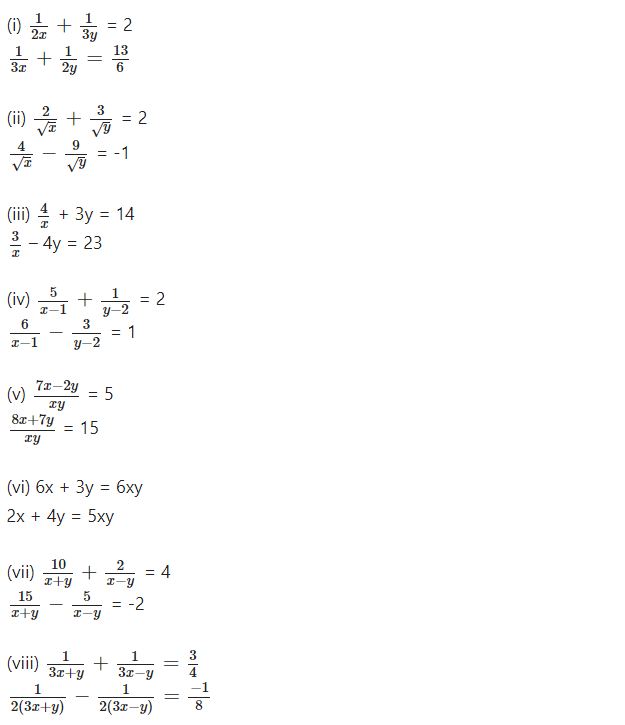


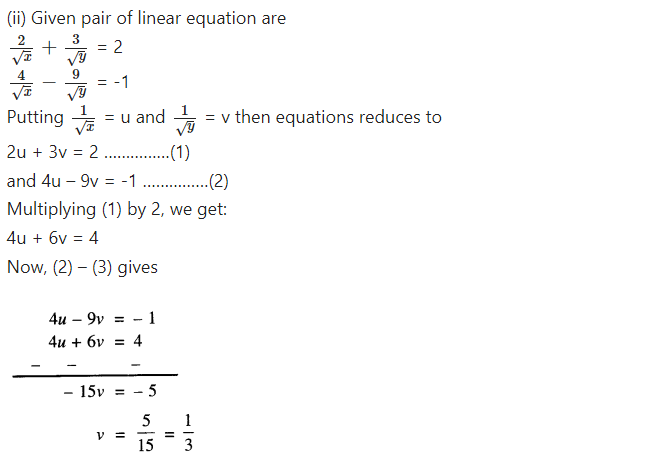

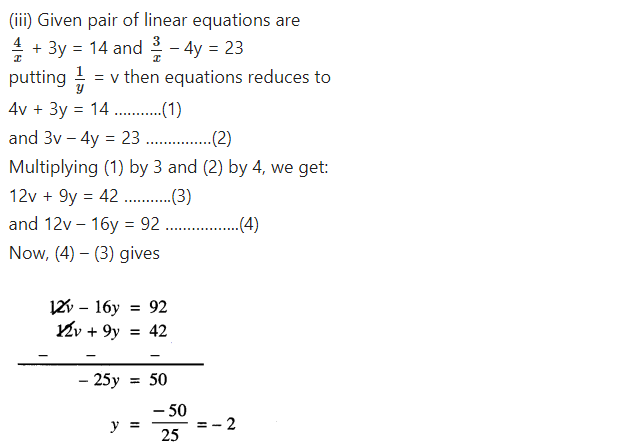
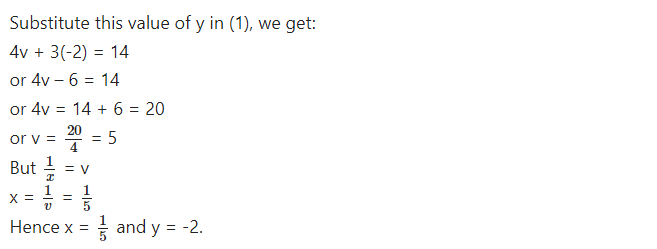
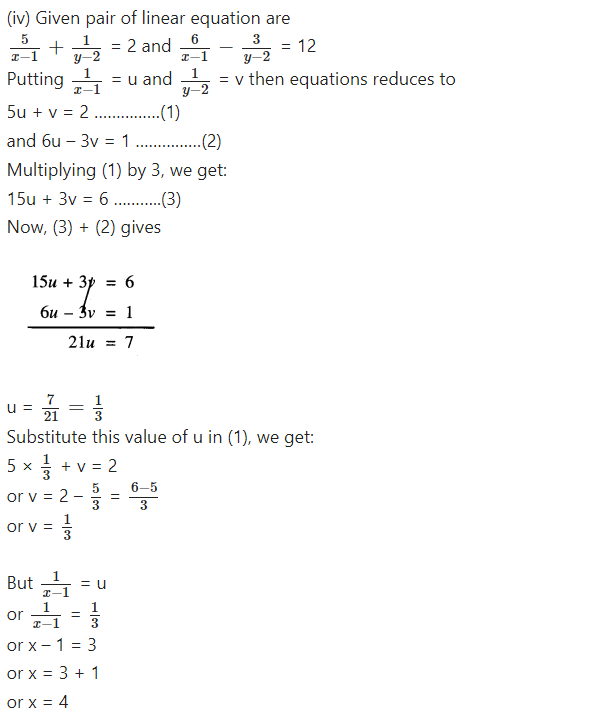








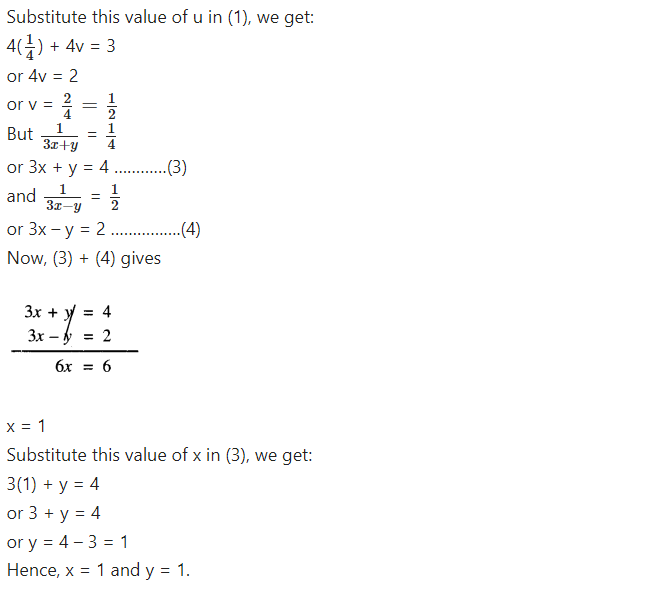
Question 2.
Formulate the following problems as a pair of equations, and hence find their solutions.
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km In 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii) Roohi travels 300 km to her home party by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
(i) Let the speed of Ritu in still water = x km/hour
and the speed of current = y km/hour
∴ speed in upstream = (x – y) km/hour
and speed in downstream = (x + y) km/hour
Distance covered by Ritu in downstream in 2 hours = Speed × Time
= (x + y) × 2 km
According to 1st condition
2(x + y) = 20
x + y = 10 ……………..(1)
Distance covered by Rim in upstream in 2 hours
= Speed × Time
= 2(x – y)km
According to 2nd condition,
2(x – y) =4
x – y = 2 ……………….(2)
Now, (1) + (2) gives
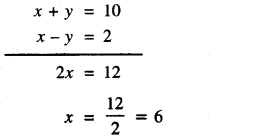
Substitute this value of x in (1), we get:
6 + y = 10
y = 10 – 6 = 4
Hence, Ritu’s speed in still water = 6 km/hour
and speed of current = 4 km/hour.




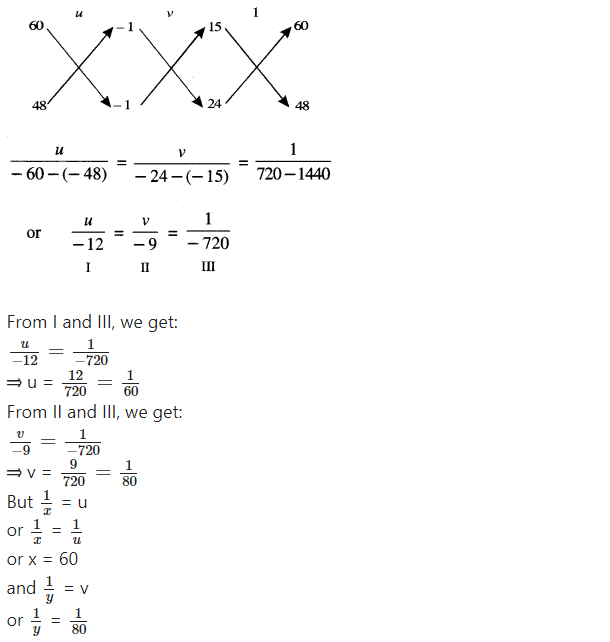
or y = 80
Hence, speed of train and bus are 60 km/hour and 80 km/hour respectively.
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here