PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4

PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4

PSEB 10th Class Maths Solutions Chapter 6 Triangles Ex 6.4

Question 1.
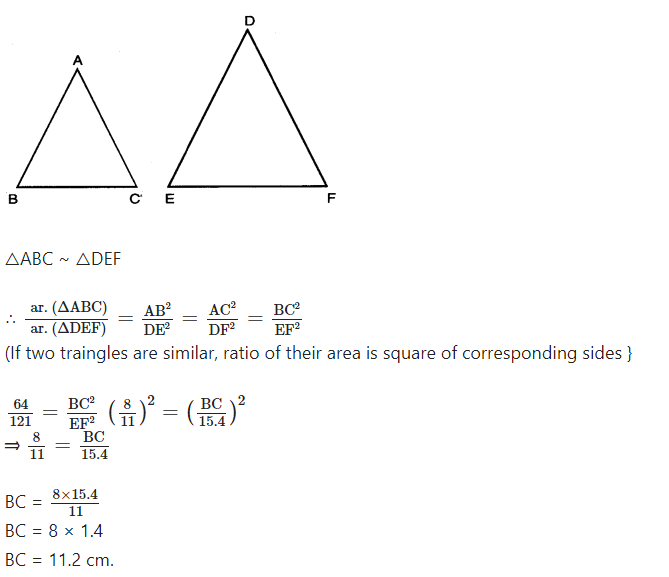
Let △ABC ~ △DEF and their areas be respectively 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:
△ABC ~ △DEF ;
area of △ABC = 64 cm²;
area of △DEF = 121 cm²;
EF= 15.4 cm

Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD. Find the ratio of the areas of traingles AOB and COD.
Solution:
ABCD is trapezium AB || DC. Diagonals AC and BD intersects each other at the point O. AB = 2 CD

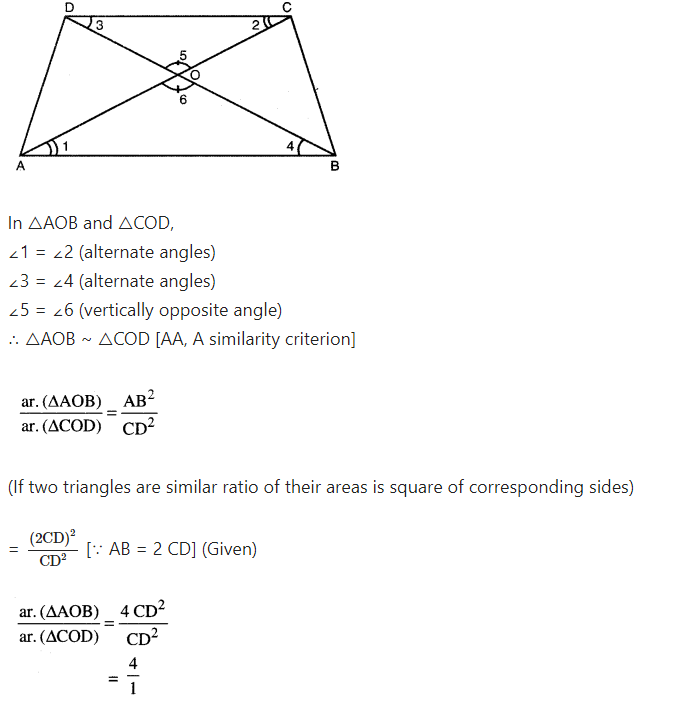
∴ Required ratio of ar △AOB and △COD = 4 : 1.

Question 3.
In the fig., △ABC and △DBC are two triangles on the same base BC. If AD intersects BC at O show that

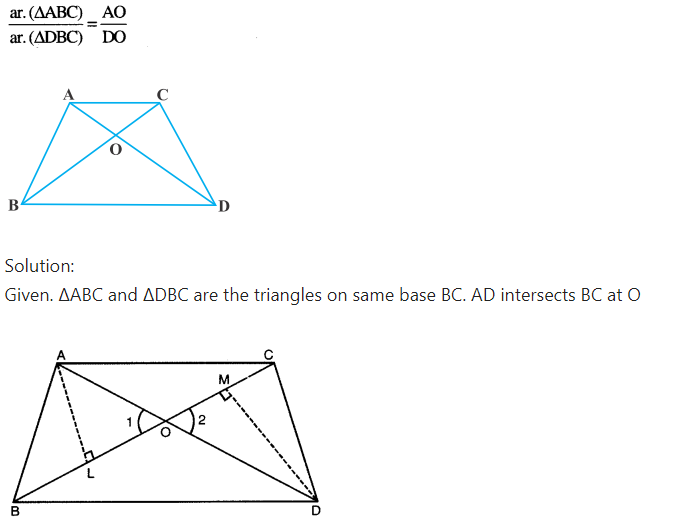
Hence proved.

Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
Given: Two ∆s ABC and DEF are similar and equal in area.
To Prove : ∆ABC ≅ ∆DEF

Question 5.
D, E and F are respectively the mid points of the sides BC, CA and AB of ∆ABC. Determine the ratio of the areas of triangles DEF and ABC.
Solution:

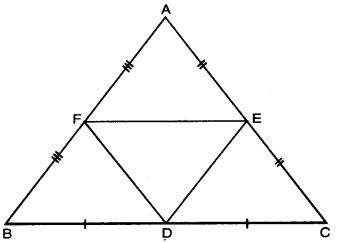
Given. D, E, F are the mid-point of the sides BC, CA and AB respectively of a tABC.
To find : ar (∆DEE) : ar (∆ABC)
Proof: In ∆ABC,
F is the mid-point of AB …(given)
E is the mid-point of AC …(given)
So, by the Mid-Foint Theorem
FE || BC and FE = 1/2 BC
⇒ FE || BD and FE = BD [∵ BD = 1/2 BC]
∴ BDEF is a || gm.
(∵ Opp. sides are || and equal)
In △s FBD and DEF,
FB = DE (opp. sides of || gm BDEF)
FD = FD .. .(common)
BD = FE
. ..(opp. sides of || gm BDEF)
∴ △FBD ≅ △DEF … (SSS Congruency Theorem)

Similary we can prove that:
△AFE ≅ △DEF
and △EDC ≅ △DEF
if △s are , then they are equal in area.
∴ ar (∆FBD) = ar. (∆DEF) ……………(1)
ar (∆AFE) = ar (∆DEF) ……………(2)
ar (∆EDC) = ar (∆DEF) ……………(3)
Now ar ∆ (ABC)
= ar (∆FBD) + ar (∆DEF) + ar (∆AFE) + ar (∆EDC)
= ar.(∆DEF) + ar (∆DEF) + ar (∆DEF) + ar. (∆DEF) [Using (1), (2) and (3)]
= 4 ar (∆DEF)
⇒ (∆DEF) = 1/4 ar(∆ABC)
⇒ ar.(ΔDEF)/ar.(ΔABC)=1/4
∴ ar (∆DEF) : ar (∆ABC) = 1 : 4.

Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Given: ∆ABC ~ ∆DEF.
AX and DY are the medians to the side BC and EF respectively.

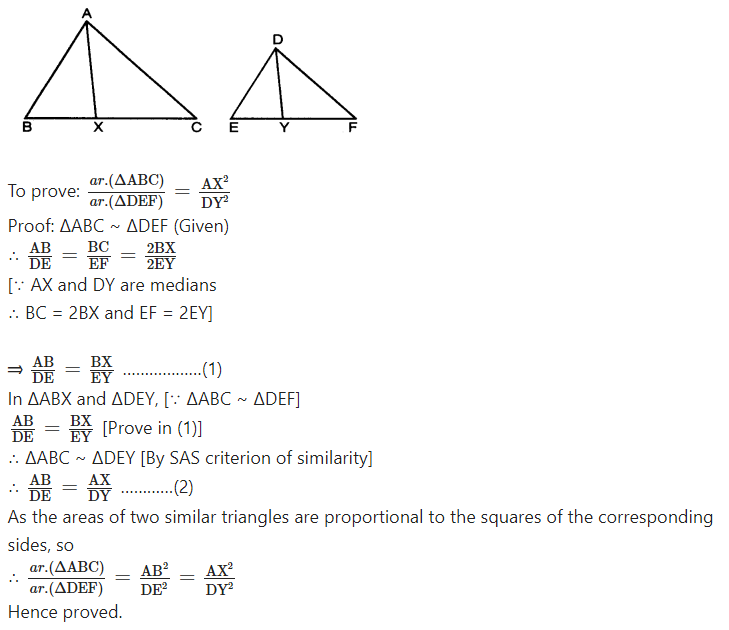
Question 7.
Prove that the areas of the equilateral triangle described on the side of a square Is half the area of the equilateral triangle described on its diagonal.
Solution:
Given: ABCD is a square. Equilateral ∆ABE is described on the side AB of the square and equilateral ∆ACF is desribed on the diagonal AC.

Question 8.
Tick the correct answer and justify: ABC and BDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4.
Solution:

Question 9.
Tick the correct answer and justify: Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are ¡n the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81.
Solution:

Follow on Facebook page – Click Here

Google News join in – Click Here

Read More Asia News – Click Here

Read More Sports News – Click Here

Read More Crypto News – Click Here