Gujarat Board Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.4
Gujarat Board Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.4
Gujarat Board Textbook Solutions Class 10 Maths Chapter 2 Polynomials Ex 2.4
Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:


2. Let p(x) = x3 – 4x2 + 5x – 2
Then, we have
p(2) = (2)3 – 4(2)2 + 5(2) – 2
= 8 – 16 + 10 – 2 = 0
p(1) = (1)3 – 4(1)2 + 5(1) – 2
= 1 – 4 + 5 – 2 = 0
Therefore, 2 and 1 are the two zeroes of x3 – 4x2 + 5x – 2. Hence (x – 2) (x – 1), i.e., x2 – 3x + 2 is a factors of the given polynomial. Now, we apply the division algorithm to the given polynomial and x2 – 3x + 2.
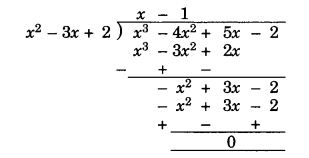
So, x3 – 4x2 + 5x – 2
= (x2 – 3x + 2) (x – 1)
⇒ x3 – 4x2 + 5x – 2 = (x – 2) (x – 1) (x – 1)
Hence, 2, 1 and 1 are the zeros of x3 – 4x2 + 5x – 2.
Comparing the given polynomial with ax3 + bx2 + cx + d, we get
a = 1
b = -4
c = 5
d = – 2
Let α = 2
β = 1
and γ = 1
Then, we have
α + β + γ = 2 + 1 + 1 = 4

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeros taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:

Question 3.
If the zeroes of the polynomial
x3 – 3x2 + x + 1 are a – b, a, a + b, find a and b.
Solution:
Then given polynomial is x3 – 3x2 + x + 1
Comparing with Ax3 + Bx2 + Cx + D, we get
A = 1
B = -3
C = 1
D = 1
Let α = a – b
β = a
γ = a + b
Then, we have
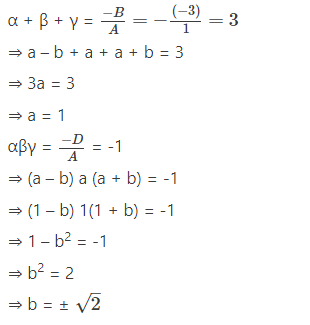

Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
Let us apply the division algorithm to the give Polynomial x4 – 6x3 + 16x2 – 25x + 10 and another Polynomial x2 – 2x + k.
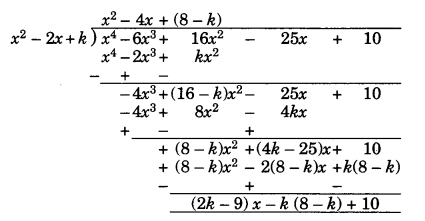
Remainder
= (2k – 9)x – k (8 – k) + 10
But the remainder is given to be x + a.
Therefore, 2k – 9 = 1
⇒ 2k = 10 ⇒ k = 5
and -k(8 – k) + 10 = a
⇒ -5(8 – 5) + 10 = a
⇒ – 5 = a
⇒ a = -5
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here