JKBOSE 9th Class Mathematics Solutions Chapter 1 Number System
JKBOSE 9th Class Mathematics Solutions Chapter 1 Number System
JKBOSE 9th Class Mathematics Solutions Chapter 1 Number System
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Number System Textbook Questions and Answers
Numbers of various types are in use in Mathematics such as Natural numbers, Whole numbers, Integers, Rational numbers, Irrational numbers, and so on. They are defined as follows :
1. Natural Numbers. The counting numbers such as 1, 2, 3, 4, 5, are called natural numbers. There is no natural number prior to 1, so it is the smallest natural number. Natural numbers are denoted by N.
2. Whole Numbers. In the set of natural numbers if we include 0, then the resulting set of numbers is known as the set of whole numbers. It is represented by W.
W = {0, 1, 2, 3, ….……….}.
3. Integers. If to natural numbers, we add 0 and their negatives, they are known as integers and the set of integers is denoted by I. Thus,
I = {…….., – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4.……………..…….}
4. Rational Numbers. Rational number is a number, which can be expressed in the form P/q where p and q are integers, without any common factor and q is not zero.
Rational number may be positive, negative or zero. Rational number p/q is positive if p and q have same signs and they are negative if they have opposite signs.
Every integer is a rational number, but every rational number is an integer is not true.
A rational number is either a terminating or non-terminating but recurring (repeating) decimal.
Note. A rational number when expressed in lowest terms having factor 2 or 5 or both in the denominator can be expressed as a terminating decimal otherwise a non-terminating recurring decimal.
Text book exercise – 1.1
1. Is zero rational number ? Can you write it in the from p/q, where p and q are integers and q ≠ 0 ?
Solution.— Yes, zero is a rational number and it can be written in the form of p/q as
0 = 0/1
here p = 0
and q = 1
Notice that q can be any number you wish. [∴ 0 = 0/2 = 0/3 etc.]
2. Find six rational numbers between 3 and 4.
Solution.— Let a = 3 and b = 4


3. Find five rational numbers between 3/5 and 4/5.
Solution.— Let a = 3/5 and b = 4/5
Rational number lying between a and b is a+b/2 i.e.

ALITER
We want to find all five at one go. Since we want 5 numbers so wriye.
3/5 = 18/30 and 4/5 = 24/30
Now five rational numbers between 3/5 and 4/5 are
19/30, 20/30, 21/30, 22/30, 23/30
4. State whether the following statements are true or false ?
(i) Every natural numbers is a whole numbers.
(ii) Every integer numbers is a whole number.
(iii) Every rational number is a whole number.
Solution.— (i) True
Justification : Since collection of whole numbers contain all the natural numbers.
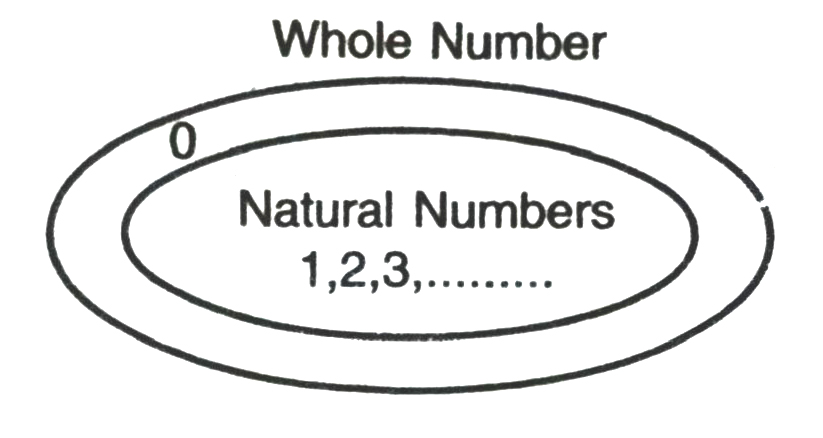
So, every whole number is not a natural number but every natural number is a whole numbers.
(ii) False
Justification : Negative numbers -3, -2, -1 are not whole numbers.

Integers whole numbers
(iii) False
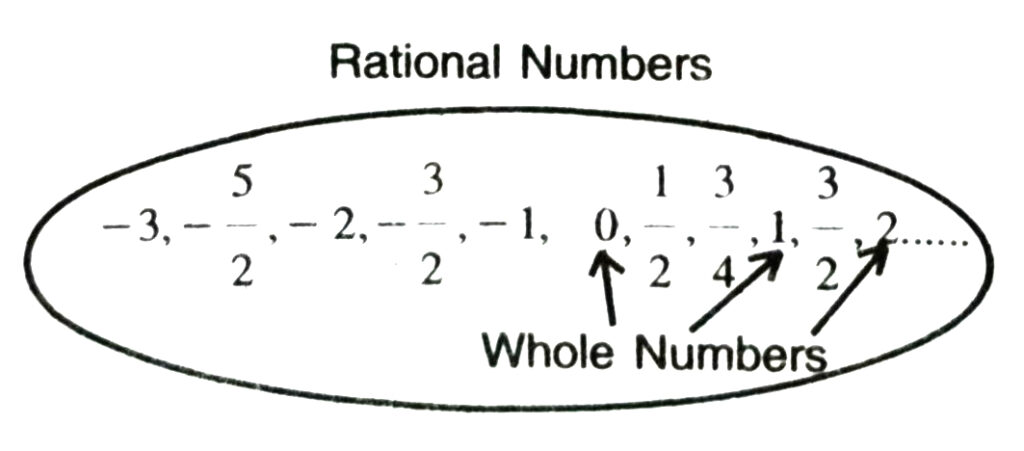
Justification : Whole numbers are the part of rational numbers.
So, every rational number is not a whole number.
For example 3/4 is a rational number but not a whole number.
IRRATIONAL NUMBERS
5. Irrational Number. A number, which is not a rational number, is called an irrational number.
A number, which cannot be expressed in the form of p/q, where p and q are integer and q ≠ 0 e.g.
√2, √3, √5 etc. irrational numbers.
The set of irrational numbers is denoted by S.
A number is irrational if and only if, its decimal representation is non-terminating and non-repeating.
π and e are non-terminating and non-repeating decimals. Hence and π are irrational numbers.
Note. (i) There are infinite many irrational numbers.
(ii) Every irrational number corresponds to a unique point on a number line.
Real numbers. All rational numbers and irrational numbers together form the set of real numbers.
Every real number is represented by a unique point on the number line and conversely, every point on the number line represents a unique real number. Further, we have a method of representing the real numbers on the number line (also called the real number line).
The system of real numbers possesses all the properties the system of rational numbers. We have to simply replace the word ‘rational’ by ‘real’. Thus if, a, b are two real numbers then a + b, a – b, a. b, a ÷ b (b ≠ 0) are also real numbers. Also either a > b or a = b or a < b.
But there is one important difference between the set of real numbers and set of rational numbers.
Every point on a number line corresponds to a real number and it is not true in case of rational numbers.
The Pythagoreans in Greece, followers of the famous mathematician and philosopher Pythagoras, were the first to discover irrational numbers around 400 BC. They called them incommensurable.

Georg Cantor was born in St. Petersburg, Russia. Cantor’s genius was to recognise that there are different kinds of infinities in mathematics. For example, he showed that there are more irrational numbers than rational numbers, even though both are infinitely many.

Richard Dedekind, constructed the irrational from the rationals using the idea of ‘cuts’ now called ‘Dedekind cuts’.

TEXT BOOK EXERCISE – 1.2
1. State whether the following statements are true or false ? Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m, where m is a natural number.
(iii) Every real number is an irrational number.
Solution.—
(i) True :
Justification : Every real number contain both rational and irrational numbers.
In other words irrational numbers are part of real numbers. That’s why the statement that every irrational number is a real number is true.
(ii) False
Justification :
…. -5, -4, -3, -2, -1 are real numbers on number line but are not the square root of any natural number.
(iii) False
Justification : All rational numbers which are real numbers but not the irrational numbers.
2. Are the square roots of all positive integers irrational ? If not, give an example of the square root of a number that is a rational number.
Solution.— No square roots of all positive integers are not irrational.
For example :
4, 9, 16, 25 … etc. are positive integers and their square roots;
√4 = 2 rational number
√9 = 3 rational number
√16 = 4 rational number
√25 = 5 rational number.
3. Show how √5 can be represented on the number line.
Solution.— For √5
∴ 5 = 22 + 12
∴ We can construct √5 as the length of hypotenuse of a right triangle whose sides are of lengths 2 and 1 unit.
Let OX be a number line on which O represent 0 and A represents 2 units length. Draw a line AB ⊥ OA and mark point B on so that AB = 1 unit.
Then OB2 = OA2 + AB2
= 22 + 12
= 4 + 1 = 5
OB = √5
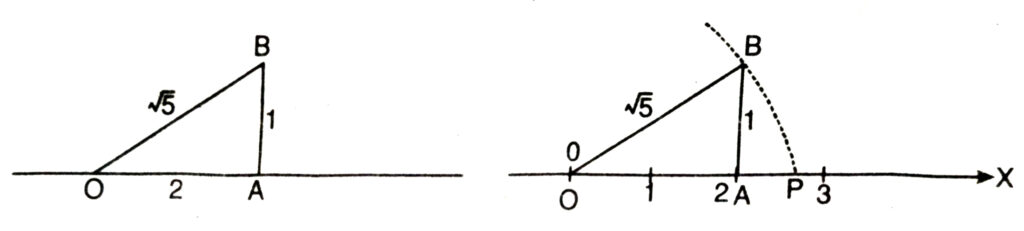
Using a compass with centre O and radius OB we mark a point P on the number line corresponds to √5 on the number line.
This P represents the irrational number √5.
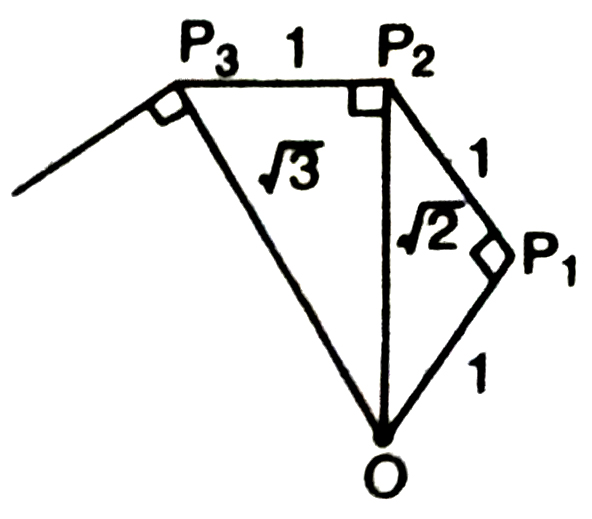
4. Classroom activity Constructing the ‘square root spiral’: Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length [see Fig.]. Now draw a line segment P2P3 perpendicular to OP2. Now draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn-1‘ In this manner, you will have created the points : O, P1, P2, P3, Pn…. and joined them to create a beautiful spiral depicting √2,√√3,√4,…. .
REAL NUMBERS AND THEIR DECIMAL EXPANSION
In this section, we are going to study rational and irrational numbers from a different point of view. We will look at the decimal expansions of real numbers and see if we can use the expansions to distinguish between rationals and irrationals. We will also explain how to visualize the representation of real numbers on the number line using their decimal expansions.
Results for decimal representation of rational numbers and irrational numbers
The decimal expansion of a rational number is either terminating or non-terminating recurring. Moreover, number whose decimal expansion is terminating or non-terminating recurring is rational.
The above statement talks about rational numbers. What about irrational numbers ? Because of the above property, we can conclude that the decimal expansions of irrational numbers are non-terminating non-recurring.
Let s = 0.101101110111110…. . Notice that it is non-terminating and non-recurring. Therefore from the above property, it is irrational. Moreover, notice that you can generate infinitely many irrationals similar to s.
What about the famous irrational √2 and л ? Here are their decimal expansions up to a certain stage.
√₂ = 1.
π = 3.
Over the years, mathematicians have developed various techniques to produce more and more digits in the decimal expansions of irrational numbers. For example, you might have learnt to find digits in the decimal expansion of √2 by the division method. Interestingly, in the Sulbasutras (rules of chord), a mathematical treatise of the Vedic period (1500 – 800 BC), you find an approximation of √2 as follows :
√2 = 1 + 1/3 + 1/4 · 1/3 – 1/34 · 1/4 · 1/3
= 1.4142156

Notice that it is the same as the one given above for the first five decimal places. The history of the hunt for digits in the decimal expansion of л is very interesting. The Greek genius Archimedes was the first to compute digits in the decimal expansion of л. He showed 3.140845 < π < 3.142857. Aryabhatta (476 – 550 AD) the great Indian mathematician and astronomer, found the value of л correct to four decimal places (3.1416). Using high speed computers and advanced algorithms, has been computed to over 1.24 trillion decimal places !
Here is a property for irrational numbers similar to the property stated earlier for rational numbers.
The decimal expansion of an irrational number is non-terminating non-recurring and a number whose decimal expansion is nonterminating non-recurring is irrational.
TEXT BOOK EXERCISE – 1.3
1. Write the following in decimal form and say what kind decimal expansion each has :

Solution.— 36/100 = 0.36 terminating decimal
(ii) 1/11
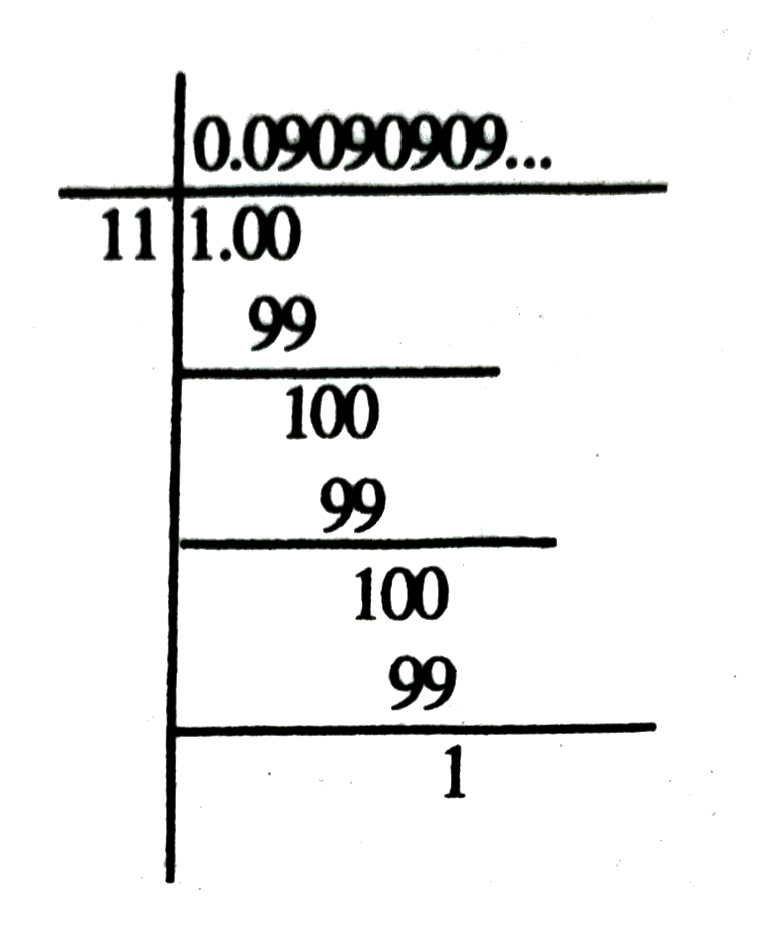
Remainders : 1, 1, 1, 1 ……..
Divisor : 11
We write 1/11 = 0.09090909
= 0.09 non-terminating repeating
Remainders : 1, 2, 4, 0
Divisor : 8
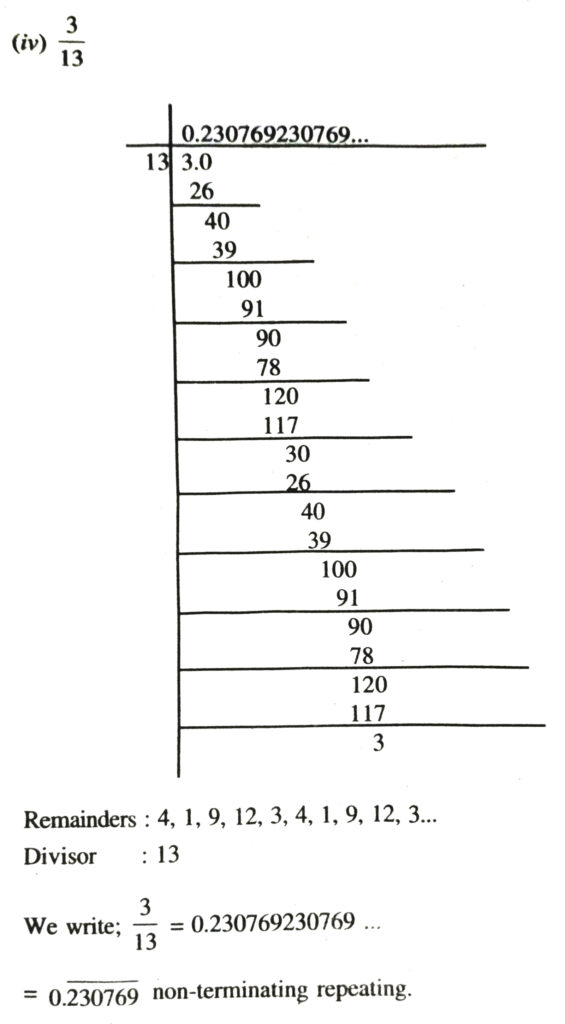
(v) 2/11
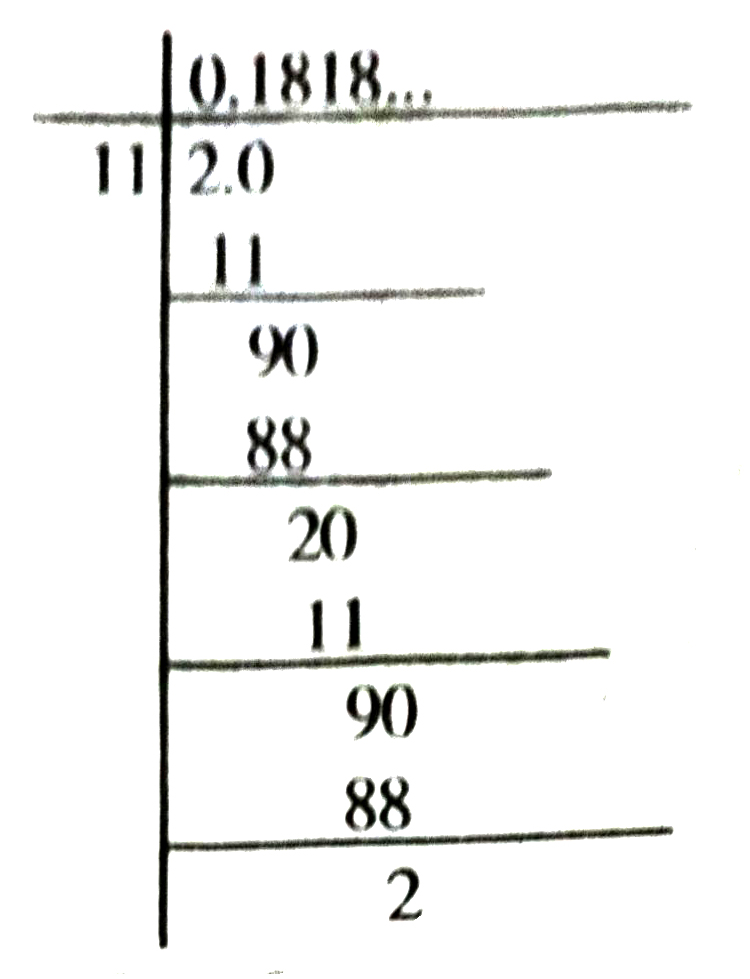
Remainders : 9, 2, 9, 2 ….
Divisor : 11
We write ; 2/11 = 0.1818 ….
= 0.18 non-terminating repeating

2. You know that 1/7 = 0.142857 · can you predict what the decimal expansions of 2/7, 3/7; 4/7, 5/7, 6/7 are without actually doing the long division ? If so, how ?
Solution.— Yes. All the above will have repeating decimals which are permutations of 1, 4, 2, 8, 5, 7. For example, here is 1/7

To find, 2/7 locate when the remainder becomes 2 and the respective quotient (here it is 2) then, write the new quotient beginning from there (the arrows drawn in the figure above using the repeating digits,
1, 4, 2, 8, 5, 7). So 2/7 = 0.285714 .
3. Express the following in the form p/q, where p and q are integers and q ≠ 0.
(i) 0.6 (ii) 0.47 (iii) 0.001.
Solution.— (i) We do not know
what 0.6 is, let us call it ‘x’.
x = 0.6666… …(1)
Multiplying both sides by 10 we get :
10x = 10 × .6666…
⇒ 10 x = 6.6666… …(2)
Subtracting (1) from (2) we get :
10x – x = (6.6666…) – (.6666…)
⇒ 9x = 6
⇒ x = 6/9
⇒ x = 2/3
(ii) Let x = 0.47
x = 0.4777… …(1)
Multiply both sides by 10 we get :
10x = 4.7777… …(2)
Subtracting (1) from (2), we get :
10x – x = (4.7777…) – (0.47777…)
⇒ 9x = 4.3
⇒ x = 4.3/9
⇒ x = 43/90
(iii) Let x = 0.001
x = 0.001001001… …(1)
Multiplying both sides by 1000 we get :
1000x = 1.001001… …(2)
Subtracting (1) from (2) we get :
1000x – x = (1.001001…) – (0.001001…)
⇒ x = 1/999
4. Express 0.99999… in the form p/q. Are you surprised by your answer ? With your teacher and classmates discuss why the answer makes sense.
Solution.— Let x = 0.99999… …(1)
Multiplying both sides by 10 we get :
10x = 9.9999… …(2)
Subtracting (1) from (2) we get :
10x – x = (9.9999…) – (0.9999…)
⇒ 9x = 9
⇒ x = 9/9
⇒ x = 1
Yes, at a glance we are surprised at our answer.
But the answer makes sense when we observe that 0.9999… goes on for ever. So there is no gap between 1 and 0.9999… and hence they are equal.
5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer.
Solution.—

Remainder at stage B is same as that of the remainder at stage A.
∴ 1/17 = 0.0588235294117647…
= 0.0588235294117647 non-terminating repeating decimal.
6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy ?
Solution.— To represent rational number p/q (q ≠ 0) in terminating decimal form it is necessary to choose denominator q such that its prime factorization must has only powers of 2 or powers of 5. For For example (i) 7/16 is a terminating decimal because 16 = 24
(ii) 11/25 is a terminating decimal
because 25 = 52
7. Write three numbers whose decimal expansions are nonterminating non-recurring.
Solution.— As we know that irrational numbers in the decimal expansion are always non-terminating and non-recurring.
Therefore,
√3 = 1.73205080756…
1√5 = 0.44721359549 …
√10 = 3.16227766016
Students may have their own answers. For example;
0.01001000100001…
0.202002000200002…
0.003000300003…
8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.
Solution.— 5/7 in decimal representation is as follows :
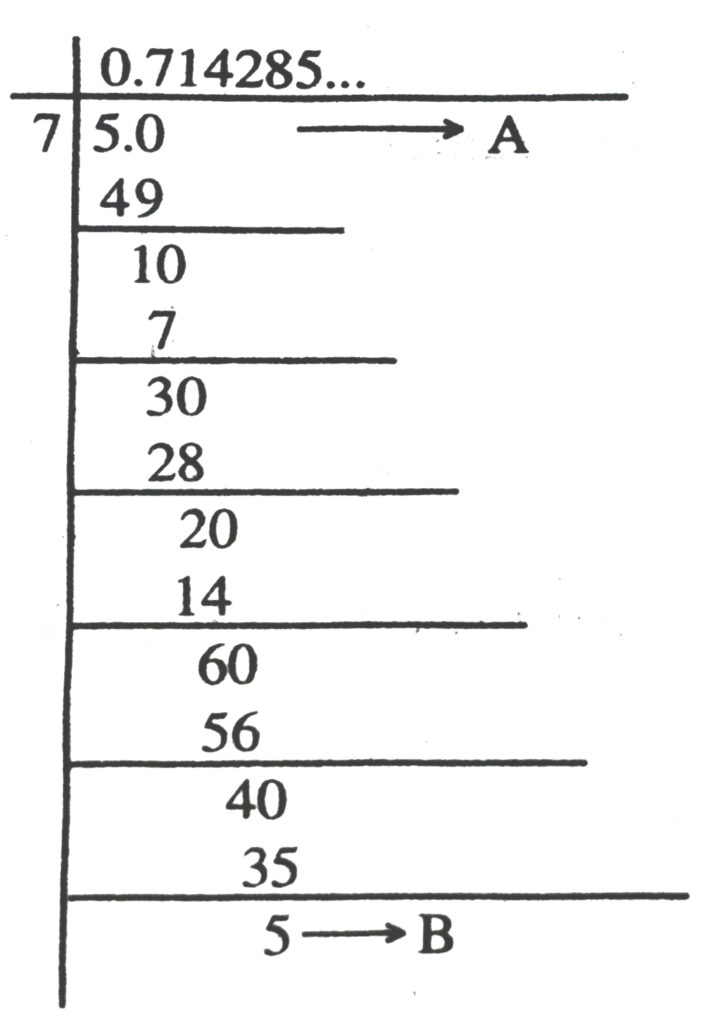
Remainder at stage B is same as that remainder of stage A.
∴ 5/7 = 0.714285
Now 9/11 in decimal representation is as follows :
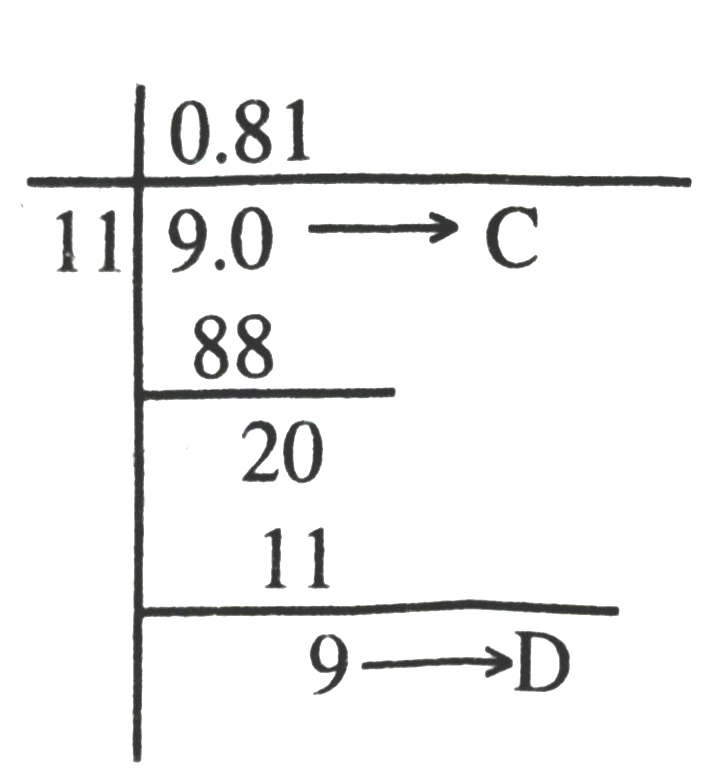
Remainder at stage D is same as that of remainder at stage C.
∴ 9/11 = 0.81
Now we can have infinite many irrational numbers between 5/7 and 9/11.
Any three of these are :
0.75075007500075000075……,
0.767076700767000…..and
0.80800800080000…..
9. Classify the following numbers as rational or irrational :
(1)√23 (ii) √225 (iii) 0.3796 (iv) 7.478478… (v) 1.101001000100001…
Solution.— (i) √23 is irrational number because 23 is prime number and prime number is not a perfect square number.
(ii) √225 is a rational number
Since √225 = √15 × 15 = 15.
(iii) 0.3796 is a rational number since it is a terminating decimal.
(iv) 7.478478… is a rational number since the decimal expansion is non-terminating repeating.
(v) 1.101001000100001… is an irrational number, since the decimal expansion is non-terminating, non-repeating.
TEXT BOOK EXERCISE -1.4
1. Visualise 3.765 on the number line, using successive magnification.
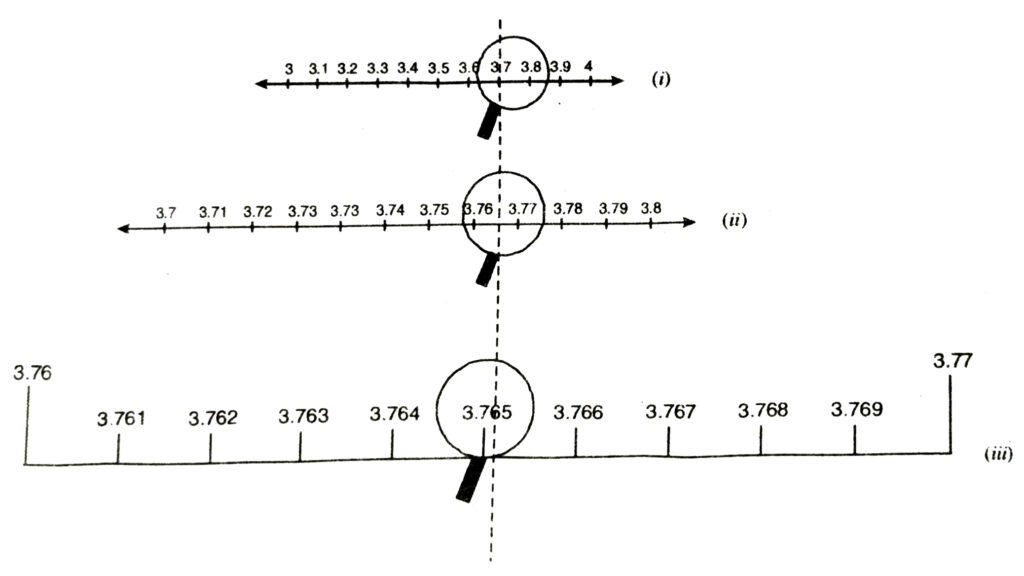
Solution.— We will proceed by successive mangnification process.
3.765 lies between 3 and 4
i.e. in the interval [3, 4].
Divide interval [3, 4] into 10 equal parts and look at [3-7, 3-8] through a magnification glass.[See fig]
Now divide [3-7, 3-8] into 10 equal parts and look [3-76, 3.77] through the magnifying glass that 3-765 lie in the interval [3.76, 3-77] [See fig]
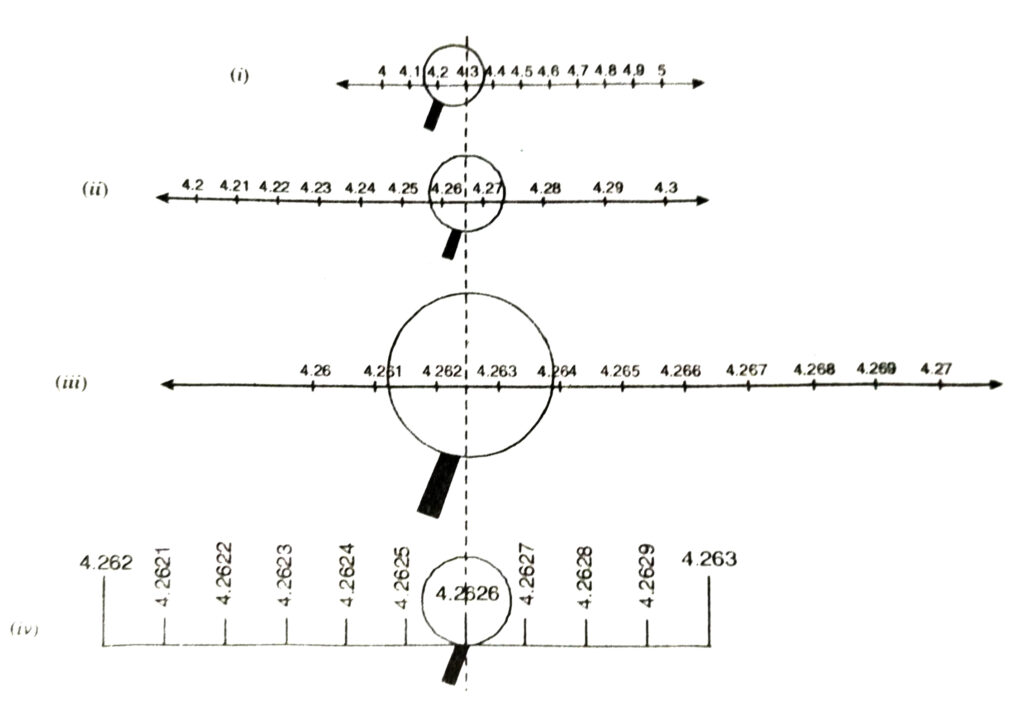
2. Visualise 4.26 on the number line, up to 4 decimal places.
Solution.— We will proceed by successive magnification process. 4-2626…… lies between 4 and 5 i.e. in the interval [4, 5]. Divide [4, 5] into 10 equal parts and look at [4.2, 4.3] through magnification glass [see fig (i)]. Now divide [4.2, 4.3] into 10 equal parts and look [4-26, 4.27] through magnification glass [see fig (ii)]. Further divide [4.26, 4.27] into 10 equal parts. Look [4.262,4-263] through magnification glass [see fig. (iii)]. Finally divide [4.262, 4.263] into 10 equal parts and look [4.262, 4.263] through magnification glass that 4-2626 lie in the interval [4-262, 4-263] see fig.
OPERATION ON REAL NUMBERS
Whenever mathematicians discover new numbers, they would like to learn how to manipulate with them. In our case, we would like to add, subtract, multiply, divide and take square roots and even nth roots of irrational numbers.
We have learnt, in earlier classes, that rational numbers satisfy the commutative, associative and distributive laws for addition and multiplication. Moreover, if we add, subtract, multiply or divide (except by zero) two rational numbers, we still get a rational number (that is, rational numbers are ‘closed’ with respect to addition, subtraction multiplication and division.) It turns out that irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication. However, we cannot be sure that the sum, difference, quotients and products of irrational numbers will be irrational. For example, (5+√2) − (√2), (2√3). (√3) and 2√13/ 5√13 are rationals.
Let us look at what happens when we add and multiply a rational number with an irrational number.
(i) The sum or difference of a rational number and an irrational number is irrational.
For example, 7 + √11, 3 – √7 and 2√17 – 7 are irrationals.
(ii) The product or quotient of a non-zero rational number with an irrational number is irrational.
For example, 2√2 and 1/√19 irrational.
SQUARE ROOTS OF REAL NUMBERS
Recall that, if a is a natural number, then √a = b means b² = a and b ≥ 0. The same definition can be extended for positive real numbers.
Let a > 0 be a real number. Then a = b means b² = a and b ≥ 0. In the previous section we saw how to represent √n for any positive integer n on the number line. We now show how to find √x for any given positive real number x geometrically.

Mark the distance x from a fixed point A on a given line to obtain a point B such that AB = x. From B mark a distance of 1 unit and mark the new point as C. Find the mid-point of AC and mark that point as O. Draw a semi-circle with centre O and radius OC. Draw a line perpendicular to AC passing through B and cutting the semi-
circle at D. Then BD = √x. We can prove this result using the Pythagoras Theorem. Notice that, the radius of the circle is x + 1/2 units. Therefore, OC = OD = x + 1/2 units. Now, OB = x – {x + 1/2} = x – 1/2.
So, by the Pythagoras Theorem, we have BD2 = {x + 1/2}2 – {x – 1/2}2 .
This construction not only shows us how to realize √x geometrically but also gives a visual proof that √x exists for all real numbers x > 0. If you want to know the position of √x on the number line, then make sure B coincides with zero and marks off BD on the line.
Rationalisation of Irrational number
When product of two irrational numbers is a rational number then each of them is called Rationalising factor of the other.
Note : (a) The rationalising factor of an irrational number is not unique. If a rationalising factor of an irrational number is known, then the product of this rationalising factor and a rational number is also the rationalising factor (R.F.) of the given irrational number.
Thus rationalising factor of an irrational number is not unique.
e.g. (i) Since 3√7 × √7 = 3 × 7 = 21 therefore, √7 is rationalising factor of 3√7. It may be noted that 2√7 is also R.F. of 3√7.
(b) It is convenient to use the simplest of rationalising factors of a given irrational number.
Rationalisation of binomial quadratic irrational number
If a and b are rational numbers which are not perfect squares, then irrational numbers √a + √b and √a – √b are said to be conjugate to each other.
(i) The product of two conjugate irrational numbers is always a rational number.
(ii) The simplest rationalising factor of binomial quadratic irrational number is its conjugate.
e.g. ∴ (√3 + √2) (√3 – √2) = 3 – 2 = 1
⇒ √3 – √2 is the simplest rationalising factor of √3 + √2.
TEXT BOOK EXERCISE – 1.5
1. Classify the following numbers as rational or irrational :
(i) 2-√5 (ii) (3+√23) – √23 (iii) 2√7/7√7 (iv) 1/√2 (v) 2π
Solution.— (i) In given number; 2 is a rational number and √5 is an irrational number. As we know that difference of a rational and irrational number is always an irrational number.
∴ 2-√5 is an irrational number.
(ii) (3 + √23) – √23 = 3 + √23 – √23
= 3 is a rational number
(iii) 2√7/7√7 = 2/7 is a rational number
(iv) 1/√2
In given number,
1 is a rational number.
√2 is an irrational number. As we know that quotient of a nonzero rational and an irrational number is always an irrational number.
So, 1/√2 is an irrational number.
(v) In given number ;
2 is a rational number and is an irrational number. As we know that product of a non zero rational number and an irrational number is always an irrational number.
So, 2π is an irrational number.
2. Simplify each of the following expressions :
(i) (3 + √3) (2 + √2)
(ii) (3 + √3) (3 – √3)
(iii) (√5 + √2)2
(iv) (√5 – √2) (√5 + √2)
Solution.— (i) (3 + √3) + (2 +√2)
= 3 × 2 + 3√2 + 2√3 + √3 × √2
= 6 + 3 √2 + 2 √3 + √6
(ii) (3 + √3) (3 – √3)
= 3 × 3 – 3√3 + 3√3 – √3 × √3
= 9 – 3
= 6
(iii) (√5 + √2)2 = (√5)2 + (√2)2 + 2√5 × √2
[∴ (a + b)2 = a2 + b2 + 2ab]
= 5 + 2 + 2√10
= 7 + 2 √10
(iv) (√5 – √2) (√5 + √2)
= (√5)2 – (√2)2
[∴ (a – b) (a + b) = a2 + b2]
= 5 – 2
= 3
3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction ?
Solution.— As we know that quotient of a non-zero rational number with irrational number or quotient of an irrational number with nonzero rational number is always an irrational number.
Here π = c/d
Therefore, there is no contradiction as either c or d are irrational hence π is an irrational number.
4. Mark √9.3 on a number line.
Solution.— Mark the distance 9.3 units from a fixed point A on a given line to obtain a point B such that AB = 9.3 units. From B mark a distance of 1 unit and call the A new point as C. Find the mid-point of AC and call that point as O. Draw a semi-circle with centre O and radius OC = 5.15 units. Draw a line perpendicular to AC passing through B cutting the semi-circle at D. Then BD = √9.3.

Mathematically Justification
OA = OC = OD = 5.15 units
[radius of semi – circle]
OB = AB – OA
= 9.3 – 5.15
⇒ OB = 4.15
In rt. ∠d ΔOBD ;
OB2 + BD2 = OD2
[Using Pythagoras theorem]
⇒ (4.15)2 + BD2 = (5.15)2
⇒ BD2 = (5.15)2 – (4.15)2
= (5.15 + 4.15) (5.15 – 4.15)
[using a2 – b2 = (a + b) (a – b)]
= (9.3) (1)
⇒ BD2 = 9.3
⇒ BD = √9.3
If we want to know the position of √9.3 on the number line then we treat line BC as number line with B as zero, C as 1 and so on. Draw an arc with B as centre and radius BD which intersects the number line
in E. Then E represents √9.3.
RATIONAL NUMBERS AS EXPONENTS
(i) If m is a positive integer and x and y are real numbers such that xm = y, then 1/ym = x.
1/ym is called the mth root of y and is written as m√y.
Using this meaning we define xm for a positive rational exponent m.
If m = 0 then xº = 1
(ii) If x is a non-zero real number, then x-m =1/xm
Laws of Exponents for Rational Exponents
If x is a positive real number and m and n are any rational exponents , then
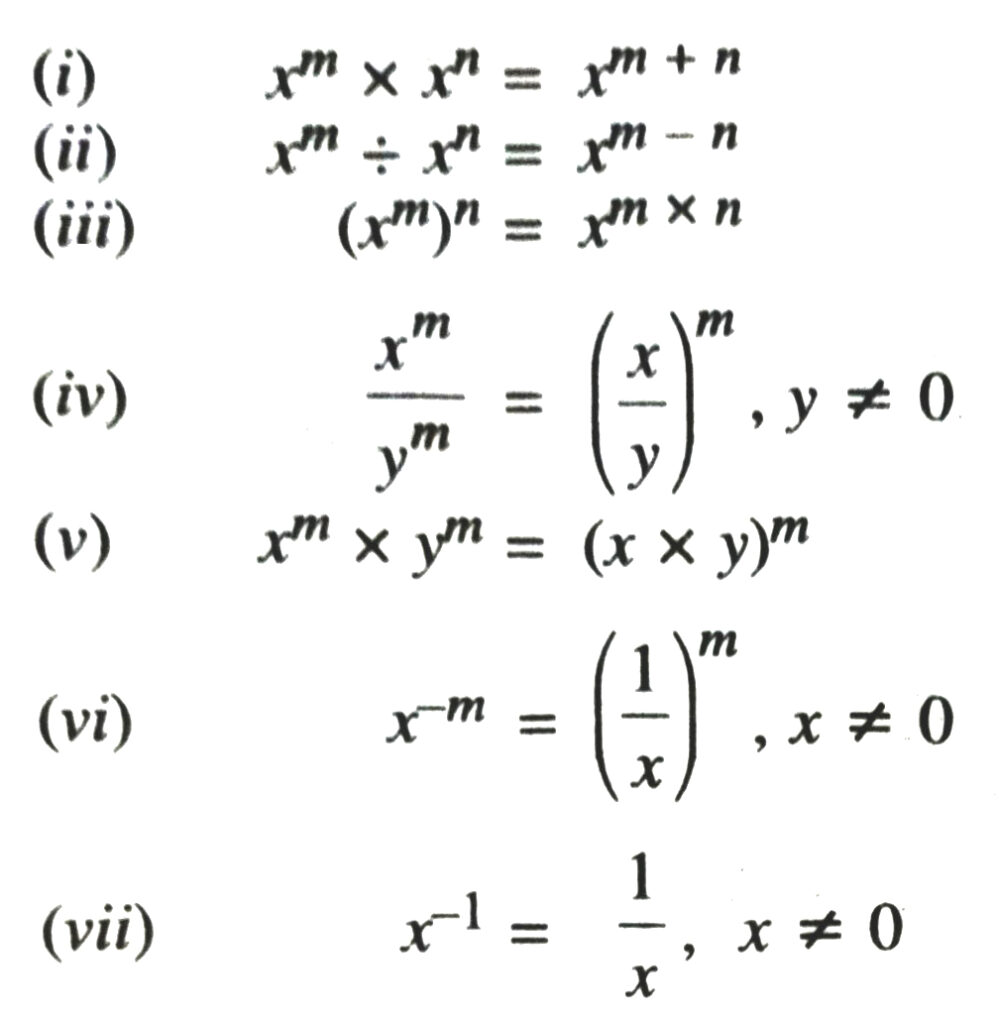
Radicals and Radicands
The sign √ is called radical sign.
For y > 0,
If x = q√y = y1/q, then is the exponential form and q√y is the radical form of x. Here, q is the index of the radical and y is the radicand.
Note that index of a radical is always positive.
TEXT BOOK EXERCISE – 1.6
1. Find : (i) 641/2 (ii) 321/5 (iii) 1251/3
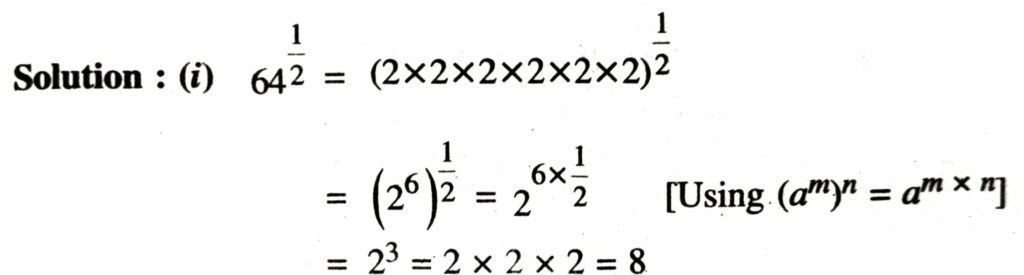
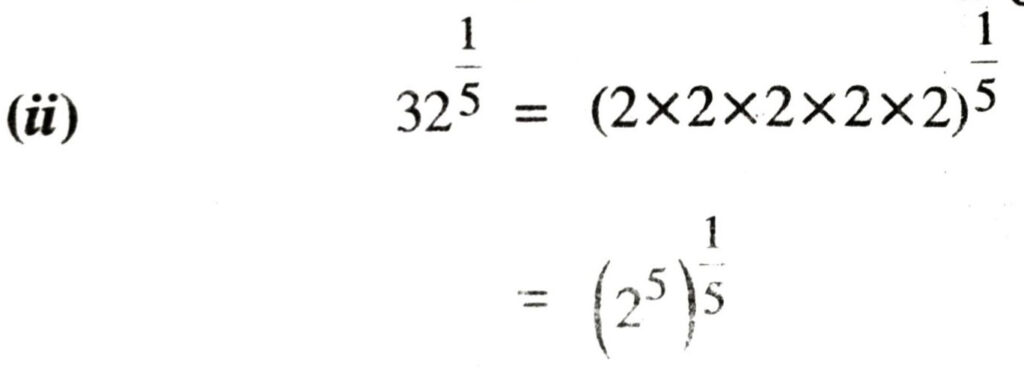

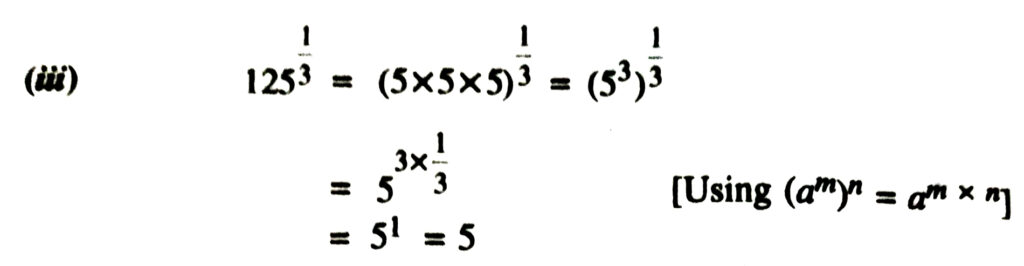

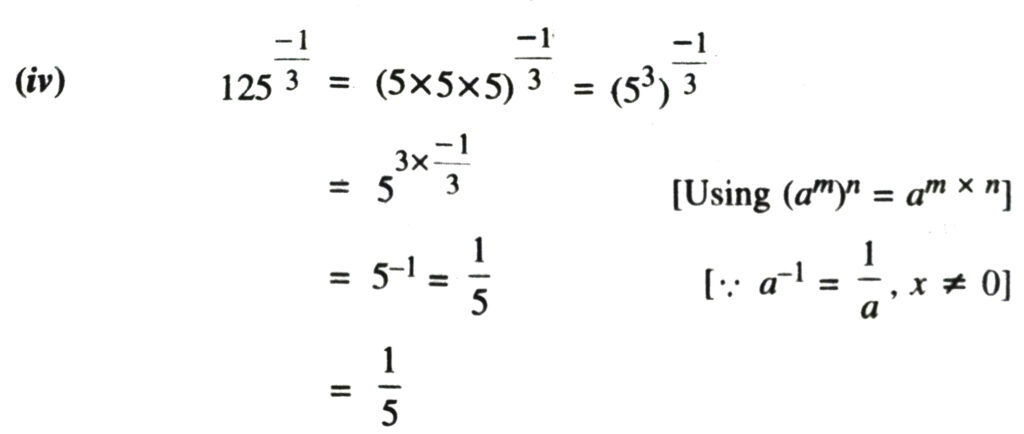

Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here