PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5

PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5

PSEB 10th Class Maths Solutions Chapter 6 Triangles Ex 6.5

Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm.
Solution:
(i) Let ∆ABC, with AB = 7 cm BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576 = 625
AC² = (25)² = 625
Now AB² + BC² = AC²
∴ ∆ABC is right angled triangle. Hyp. AC = 25cm.

(ii) Let ∆PQR with PQ = 3 cm, QR = 8 cm PR = 6 cm
PQ² + PR² = (3)² + (6)²
= 9 + 36 = 45
QR² = (8)² = 64.
Here PQ² + PR² ≠ QR²
∴ ∆PQR is not right angled triangle.

(iii) Let ∆MNP, with MN =50 cm, NP = 80 cm, MP = 100 cm
MN ²+ NP² = (50)² + (80)²
= 2500 + 6400 = 8900
MP² = (100)² = 10000
Here MP² ≠ MN² + NP².
∴ ∆MNP is not right angled triangle.

(iv) Let ∆ABC, AB = 13 cm, BC = 12 cm, AC = 5 cm
BC² + AC² = (12)² + (5)²
= 144 + 25 = 169
AB² = (13)² = 169
∴ AB² = BC² + AC²
∆ABC is right angled triangle.
Hyp. AB = 13 cm.

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM . MR.
Solution:
Given: ∆PQR is right angled at P and M is a point on QR such that PM ⊥ QR.
To prove : PM² = QM × MR

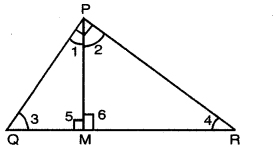
Proof: ∠P = 90° (Given)
∴ ∠1 + ∠2 = 90°
∠M = 900 (Given)
In ∆PMQ,
∠1 + ∠3 + ∠5 = 180°
=> ∠1 + ∠3 = 90° [Angle Sum Property] ………….(2) [∠5 = 90°]

Question 3.
In fig., ABD is a triangle right angled at A and AC ⊥ BD. Show that

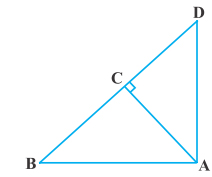
(i) AB² = BC.BD
(ii) AC² = BC.DC
(üi) AD² = BD.CD.
Solution:
Given. A right angled ∆ABD in which right angled at A and AC ⊥ BD.
To Prove:
(i) AB² = BC.BD
(ii) AC² = BC.DC .
(iii) AD² = BD.ÇD .
Proof. In ∆DAB and ∆DCA,
∠D = ∠D (common)
∠A = ∠C (each 90°)
∴ ∆DAB ~ ∆DCA [AA similarity]
In ∆DAB and ∆ACB,
∠B = ∠B (common)
∠A = ∠C . (each 90°)
∴ ∆DAB ~ ∆ACB, .
From (1) and (2),
∆DAB ~ ∆ACB ~ ∆DCA.
(i) ∆ACB ~ ∆DAB (proved)

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:
Given: ABC is an isosceles triangle right angled at C.
To prove : AB² = 2AC².
Proof: In ∆ACB, ∠C = 90° & AC = BC (given)

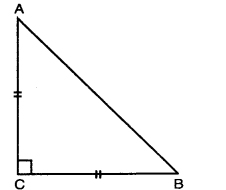
AB² = AC² + BC²
[By using Pythagoras Theorem]
=AC² + AC² [BC = AC]
AB² = 2AC²
Hence proved.

Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is right triangle.
Solution:
Given: ∆ABC is an isosceles triangle AC = BC
To prove: ∆ABC is a right triangle.

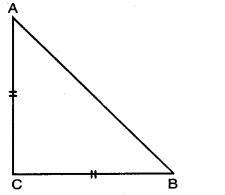
Proof: AB² = 2AC² (given)
AB² = AC² + AC²
AB² = AC² + BC² [AC = BC]
∴ By Converse of Pythagoras Theorem,
∆ABC is right angled triangle.

Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:
∆ABC is equilateral triangle with each side 2a
AD ⊥ BC
AB = AC = BC = 2a
∆ADB ≅ ∆ADC [By RHS Cong.]
∴ BD = DC = a [c.p.c.t]

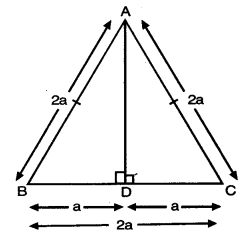
In right angled ∆ADB
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² – a² = AD².
AD² = 3a²
AD = √3a.

Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals. [Pb. 2019]
Solution:
Given: Rhombus, ABCD diagonal AC and BD intersect each other at O.
To prove:
AB² + BC² + CD² + AD² = AC² + BD²
Proof:The diagonals of a rhombus bisect each other at right angles.

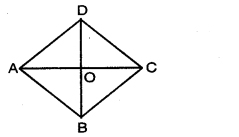
∴ AO = CO, BO = DO
∴ ∠s at O are rt. ∠s
In ∆AOB, ∠AOB = 90°
∴ AB² = AO² + BO² [By Pythagoras Theorem] …………..(1)
Similarly, BC² = CO² + BO² ……………..(2)
CD² = CO² + DO² ……………(3)
and DA² = DO² + AO² ……………….(4)
Adding. (1), (2), (3) and (4), we get
AB² + BC² + CD² + DA² = 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO²
[∵ AO = CO and BO = DO]
= (2AO)² + (2BO)² = AC² + BD².

Question 8.
In fig., O is a point In the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii)AF² + BD² + CE² = AE² + CD² + BF².

Solution:
Given: A ∆ABC in which OD ⊥ BC, 0E ⊥ AC and OF ⊥ AB.

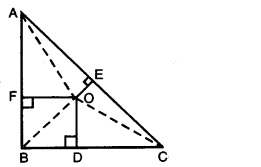
To prove:
(i) AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii) AF² + BD² + CE² = AE² + CD² + BF².
Construction: Join OB, OC and OA.
Proof: (i) In rt. ∠d ∆AFO, we have
OA² = OF² + AF² [By Pythagoras Theorem]
or AF² = OA² – OF² …………..(1)

In rt. ∠d ∆BDO, we have:
OB² = BD²+ OD² [By Pythagoras Theorem]
⇒ BD² = OB² – OD² …………..(2)

In rt. ∠d ∆CEO, we have:
OC² = CE² + OE² [By Pythagoras Theorem]

⇒ CE² = OC² – OE² ……………(3)

∴ AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – 0E²
[On adding (1), (2) and (3)]
= OA² + OB² + OC² – OD² – OE² – OF²
which proves part (1).
Again, AF² + BD² + CE² = (OA² – OE²) + (OC² – OD²) + (OB² – OF²)
= AE² + CD² + BF²
[∵AE² = AO² – OE²
CD² = OC² – OD²
BF² = OB² – OF²].

Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution:
Height of window from ground (AB) = 8m.

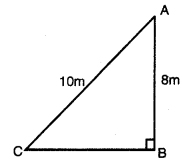
Length of ladder (AC) = 10 m
Distance between foot of ladder and foot of wall (BC) = ?
In ∆ABC,
AB² + BC² = AC² [By Pythagoras Theorem]
(8)² + (BC)² = (10)²
64 + BC² = 100
BC² = 100 – 64
BC = √36
BC = 6 cm.
∴ Distance between fóot of ladder and foot of wall = 6 cm.

Question 10.
A guy wire attached to a vertical pole of height 18 m Is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:
Let AB is height of pole (AB) = 18 m
AC is length of wire = 24 m

Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two pLanes after 1½ hours?
Solution:
Speed of first aeroplane = 1000km/hr.

Question 12.
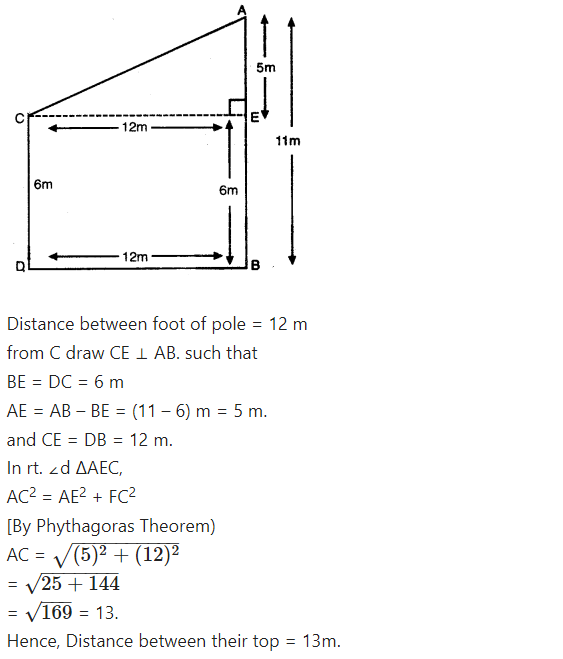
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the
distance between their tops.
Solution:
Height of pole AB = 11 m
Height of pole (CD) = 6 m

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.
Prove that AE² + BD² = AB² + DE².
Solution:
Given: In right angled ∆ABC, ∠C = 90° ;
D and E are points on sides CA & CB respectively.
To prove: AE² + BD² = AB² + DE²
Proof: In rt. ∠d ∆BCA,
AB² = BC² + CA² …………..(1) [By Pythagoras Theorem]

In rt. ∠d ∆ECD,
DE² = EC² + DC² ……………….(2) [By Pythagoras Theorem]
In right angled triangle ∆ACE,
AE² = AC² + CE² ……………….(3)
In right angled triangle ∆BCD
BD² = BC² + CD² ……………….(4)
Adding (3) and (4),
AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²]
= AB² + DE²
[From (1) and (2)]
Hence 2 + BD² = AB² + DE².
Which is the required result.

Question 14.
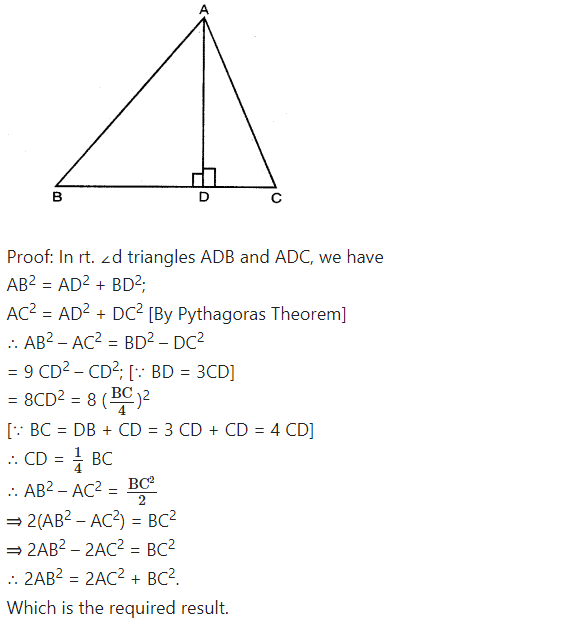
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3 CD. Prove that 2AB² = 2AC² + BC².

Solution:
Given: ∆ABC, AD ⊥ BC
BD = 3CD.
To prove: 2AB² = 2AC² + BC².

Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9 AD² = 7 AB².
Solution:
Given: Equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC.
To prove: 9AD² = 7 AB².
Construction: AB ⊥ BC.
Proof: ∆AMB ≅ ∆AMC [By R.HS. Rule since AM = AM and AB = AC]

Question 16.
In an equilateral triangle, prove that three times the square of one side Ls equal to four times the square of one of its
altitudes.
Solution:
Given:
ABC is equilateral ∆ in which AB = BC = AC

To prove: 3 AB² = 4 AD²
Proof: In right angled ∆ABD,
AB² = AD² + BD² (Py. theorem)
AB² = A BD² (Py. theorem)

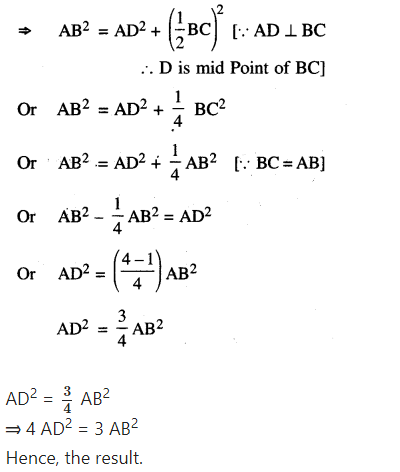
Question 17.
Tick the correct answer and justify: In ∆ABC, AB = 6 cm, AC = 12 cm and BC = 6√3 cm. [The angles of B are respectively
(A) 120°
(B) 64°
(C) 90°
(D) 45°
Solution.
AC = 12 cm
AB = 6√3 cm
BC = 6 cm
AC² = (12)² = 144 cm
AB² + BC² = (6√3)² + (6)²
= 108 + 36
AB√3 + BC√3 = 144
∴ AB√3 + BC√3 = AC√3
Hence by converse of pythagoras theorem ∆ABC is right angred triangle right angle at B
∴ ∠B = 90°
∴ correct option is (C).

Follow on Facebook page – Click Here

Google News join in – Click Here

Read More Asia News – Click Here

Read More Sports News – Click Here

Read More Crypto News – Click Here