PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6

PSEB Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.6

PSEB 10th Class Maths Solutions Chapter 6 Triangles Ex 6.6

Question 1.
In figure, PS is bisector of ∠QPR of ∆PQR. Prove that = QS/SR=PQ/PR.

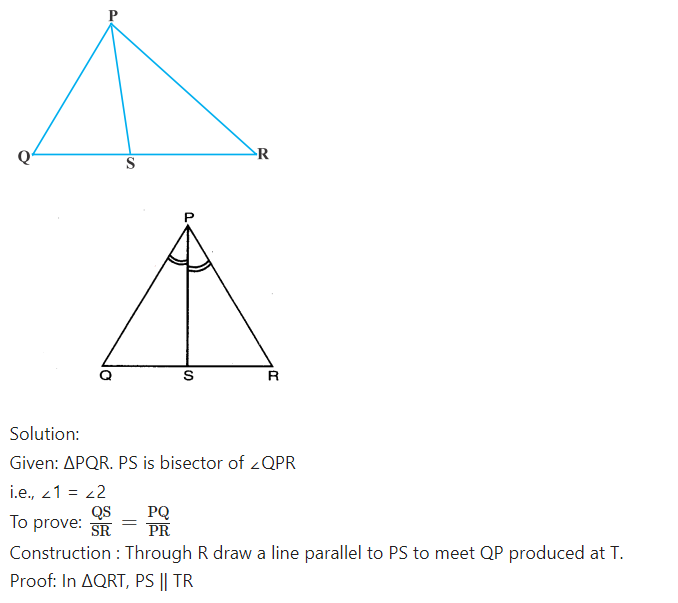
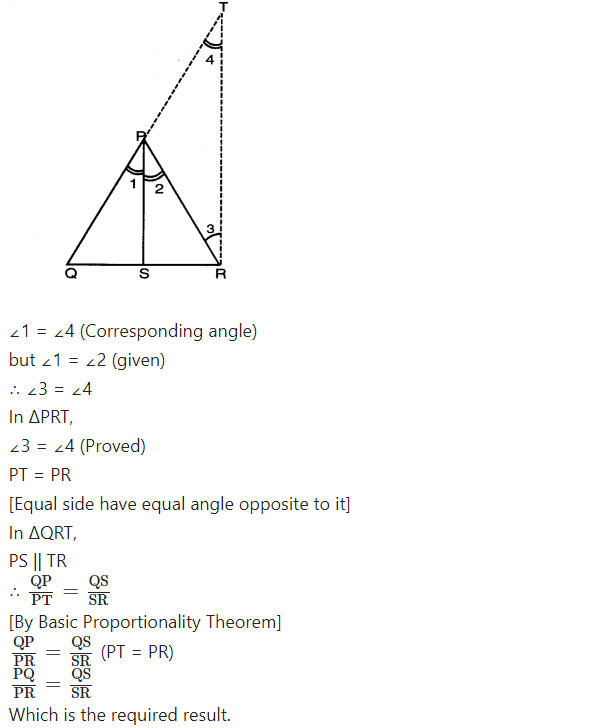
Question 2.
In the given fig., D is a point on hypotenuse AC of ∆ABC, DM ⊥ BC, DN ⊥ AB, prove that:
(i) DM² = DN.MC
(ii) DN² = OMAN.

Solution:
Given: ∆ABC, DM ⊥ BC, DN ⊥ AB
To prove: DM² = DN . AC
DN² = DM . AN.
Proof: BD ⊥ AC (Given)
⇒ ∠BDC = 90°
⇒ ∠BDM + ∠MDC = 90°
In ∠DMC, ∠DMC = 90°
[∵ DM ⊥ BC (Given)]
⇒ ∠C + ∠MDC = 90°
From (1) and (2),
∠BDM + ∠MDC = ∠C + ∠MDC
∠BDM =∠C
[Cancelling ∠MDC from both sides]
Now in ∆BMD and ∆MDC,
∠BDM = ∠C [Proved)
∠BMD = ∠DMC [Each 90°]
∆BMD ~ ∆MDC [By AA criterion of similarity]
⇒ DM/BM=MC/DM
[∵ Corresponding sides of similar triangles are proportional]
⇒ DM² = BM × MC
⇒ DM² = DN × MC [∵ BM = DN]
Similarly, ∆NDA ~ ∆NBD
⇒ DN/BN=AN/DN
[∵ Corresponding sides of similar triangles are próportional]
⇒ DN² = BN × AN
⇒ DN² = DM × AN .
Hence proved.

Question 3.
In fig., ABC is triangle in which ∠ABC > 90° and AD ⊥ BC produced, prove that AC² = AB² + BC² + 2BC.BD.

Solution:
Given: ∠ABC, AD ⊥ BC when produced, ∠ABC > 90°.
To prove : AC² = AB² + BC² + 2BC. BD.
Proof: Let BC = a,
CA = b,
AB = c,
AD = h
and BD = x.
In right-angled ∆ADB,
Using Pythagoras Theorem.
AB² = BD² + AD²
i.e., c² = x² + h²
Again, in right-angled AADC,
AC² = CD² + AD²
i.e.. b² = (a + x)² + h²
= a² + 2ax + x² + h²
= a² + 2ax + c²; [Using (1)]
b² = a² + b² + 2w.
Hence, AB² = BC² + AC² + 2BC × CD.

Question 4.
In fig., ABC is a triangle in which ∠ABC < 90°, AD ⊥ BC, prove that AC² = AB² + BC² – 2BC.BD.

Solution:
Given: ∆ ABC, ∠ABC < 90°, AD ⊥ BC.
To prove : AC² = AB² + BC² – 2BC BD.
Proof: ADC is right-angled z at D
AC² = CD² + DA² (Pythagora’s Theorem) ……………..(1)
Also, ADB is right angled ∆ at D
AB² = AD² + DB² ……………….(2)
From (1), we get:
AC² = AD² + (CB – BD)²
= AD² + CB² + BD² – 2CB × BD
or AC² = (BD² + AD²) + CB² – 2CB × BD
AC² = AB² + BC² – 2BC × BD. [Using (2)]

Question 5.
In fig., AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

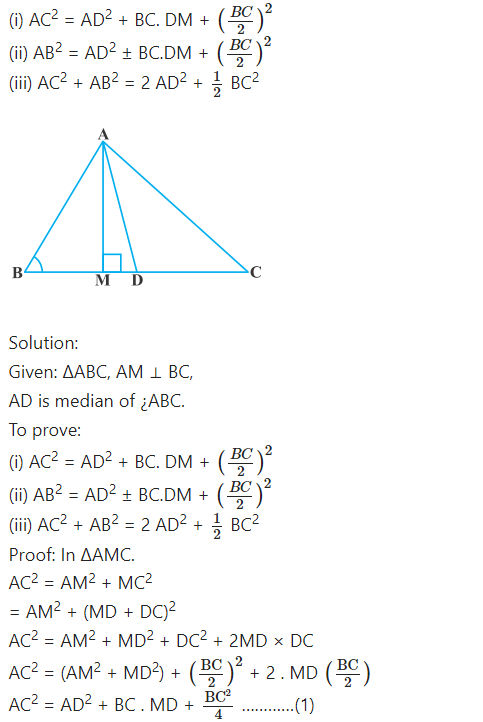
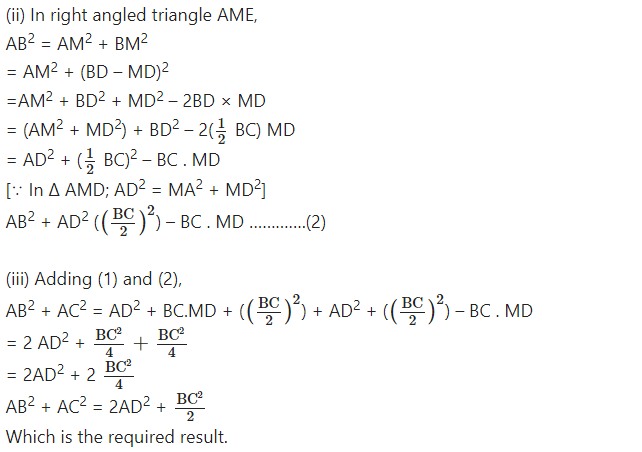
Question 6.
Prove that sum of squares of the diagonals of a parallelogram is equal to sum of squares of its sides.
Solution:

Hence, sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.

Question 7.
In fig., two chords AB and CD intersect each other at the point P prove that:
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.

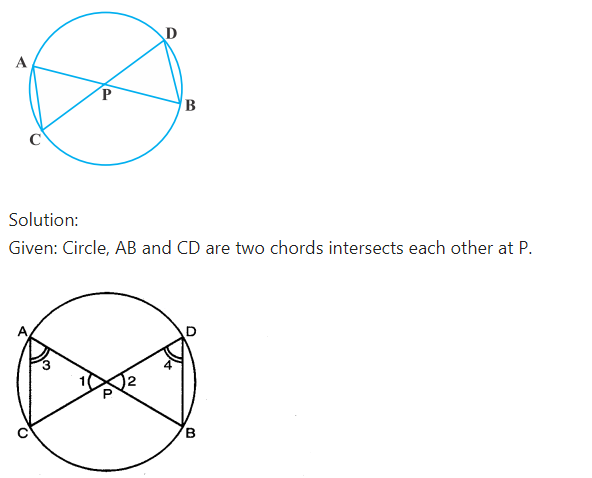
To prove:
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.
Proof:
(i) In ∆APC and ∆DPB,
∠1 = ∠2 (Vertically opposite angle)
∠3 = ∠4 (angle on same segment)
∴ ∆APC ~ ∆DPB [AA similarity criterion]

(ii) ∆APC ~ ∆DPB (Proved above)
AP/DP=PC/PB
(If two triangles are sitnilar corresponding sides are proportional)
AP.PB = PC.DP
Which is the required result.

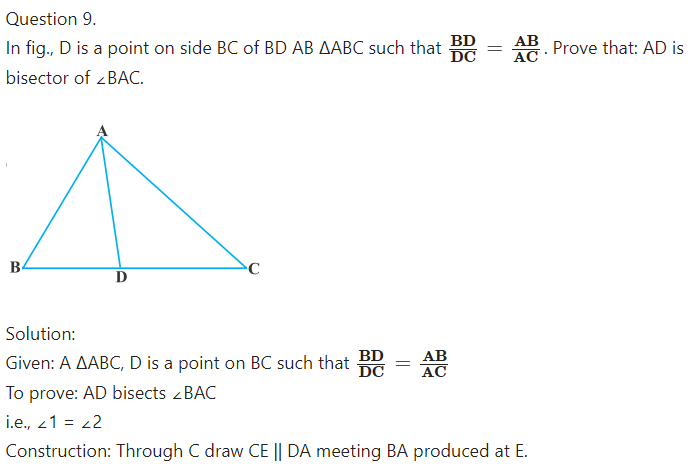
Question 8.
In fig., two chords AB and CD of a circle intersect each other at point P (when produced) outside the circle prove:
(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD.

Solution:
Given: AB and CD are two chord of circle intersects each other at P (when produced)
To prove:
(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD.
Proof:
(i) In ∆PAC and ∆PDB,
∠P = ∠P (Common)
∠PAC = ∠PDB.
(Exterior angle of cyclic quadrilqteral is equal to interior opposite angle)
∴ ∆PAC ~ ∆PDB [AA similarity criterion]

(ii) ∆PAB ~ ∆WDB
∴ PA/PD=PC/PB
[If two triangles are similar corresponding sides are proportional]
PA × PB = PC × PD.

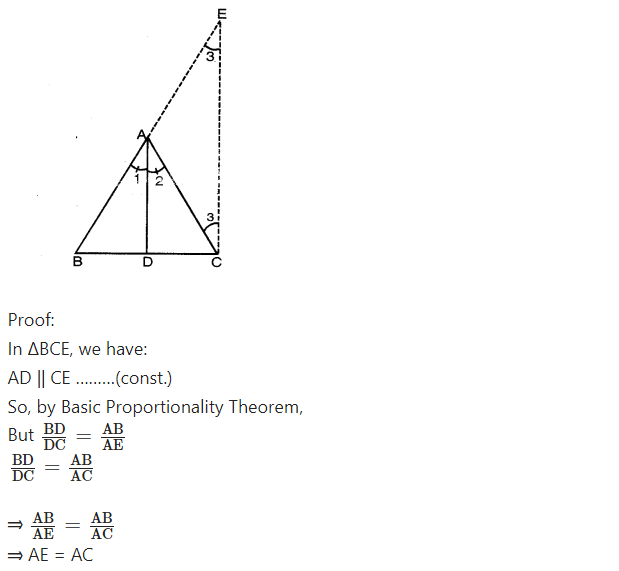
In ∆ACE, we have:
AE = AC
⇒ ∠3 = ∠4 ………. (∠s opp. to equal sides)
Since CE || DA and AC cuts them, then:
∠2 = ∠4 ……….(alt ∠s)
Also CE || DA and BAE cuts them, then:
∠1 = ∠3 …………(Corr. ∠s)
Thus we have:
∠3 = ∠4
⇒ ∠3 = ∠1
But ∠4 = ∠2
⇒ ∠1 = ∠2.
HenCe AD bisects ∠BAC.

Question 10.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out? If she pulls in the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds?

Solution:
A right angled triangle, ABC, in which,
AB = 1.8 cm,
BC = 2.4 cm.
∠B = 90°
By Pythagoras Theorem,
AC² = AB² + BC²
AC² = (1.8)² + (2.4)²
AC² = 3.24 + 5.76 =9
AC² = (3)²
AC = 3 cm
Now, when Nazima pulls in the string at the rate of 5 cm/sec ; then the length of the string decrease = 5 × 12 = 60 cm
= 0.6 m in 12 seconds.
Let after 12 seconds, position of the fly will be at D.
∴ AD = AC – distance covered in 12 seconds
AD = (3 – 0.6) m
AD = 2.4 m
Also, in right angled ∆ABD,
Using Pythagoras Theorem,
AD² = AB² + BD²
(2.4)² = (1.8)² + BD²
BD² = 5.76 – 3.24
BD² = 2.52 m
BD = 1.587 m.
∴ Horizontal distance of the fly from Nazima = BD + 1.2 m
= (1.587 + 1.2) m
= 2.787 m
= 2.79 m
Hence, original length of string and horizontal distance of the fly from Nazima is 3 m and 2.79 m.

Follow on Facebook page – Click Here

Google News join in – Click Here

Read More Asia News – Click Here

Read More Sports News – Click Here

Read More Crypto News – Click Here