JKBOSE 9th Class Science Solutions Chapter 4 Gravitation
JKBOSE 9th Class Science Solutions Chapter 4 Gravitation
JKBOSE 9th Class Science Solutions Chapter 4 GRAVITATION
Jammu & Kashmir State Board JKBOSE 9th Class Science Solutions
J&K class 9th Science Gravitation Textbook Questions and Answers
BASIS AND BASICS
◆ Everybody in this universe attracts every other body towards it with a force called Force of Gravitation.
◆ The revolution of the moon around the earth and the falling down of a body projected upward is due to force of gravitation.
◆ Gravitation is a weak force unless it may not involve bodies having greater masses.
◆ The attractive force due to earth is called force of gravity.
◆ Law of gravitation states that the force of attraction between two objects is directly proportional to the product of their masses and inversely proportional to the square of distance between their centres.
This force always acts along the line joining the centres of two objects.
◆ The law of gravitation is a universal law which means that this law applies to all minha Jisko big and small objects.
◆ The magnitude of the force acting between the earth and the objects lying on the surface of earth is given by formula F = GMm / d2 where G = 6.673 × 10-11 N – m²/kg²
◆ The acceleration produced in the body due to force of gravity is called acceleration due to gravity. It is denoted by ‘g’.
◆ The value of ‘g’ is more on the poles than on the equatorial line.
◆ Force of gravity decreases with the increase of height above the surface of earth.
◆ Kepler gave the following three laws which govern the motion of the planets :
(i) The planetary path of each planet is elliptical at the centre of which the sun ad is situated.
(ii) The line joining sun and the planet sweeps equal area in equal interval of time.
(iii) The cube of average distance ‘r’ of a planet from the sun is inversely proportional to the square of the orbital period ‘T’ of that planet.
◆ The quantity of matter present in an body is called the mass of the body. Mass is the measure of inertia of the body. The mass of a body remains constant at all places.
◆ The weight of a body is the force with which the body is attracted towards the centre of the earth
IMPORTANT TERMS/FACTS TO MEMORISE
⇒ Force of Gravitation. It is that force with which two bodies attract each other but they are lying apart.
⇒ Universal law of Gravitation. The mutual force of attraction between every two bodies in this universe is directly proportional to the product of the masses of the two bodies and inversely proportional to the square of the distance between them. This force acts along the line joining the centres of the two bodies.
⇒ Acceleration due to Gravity. Acceleration produced in the bodies falling freely under the action of gravity is called acceleration due to gravity.
⇒ Force of Gravity. It is the force with which earth attracts all bodies towards its centre.
⇒ Weight. The force with which the earth attracts bodies towards it is called weight.
⇒ Mass. The quantity of matter contained in the body is called its mass.
⇒ Inertial Mass. This mass measures the resistance which is produced due to change in the position of rest to motion.
⇒ Universal Gravitational Constant. It is the force which acts between two bodies each of unit mass and lying unit distance apart.
⇒ Kepler’s first law. All planets move around the sun in elliptical orbits. Kepler’s second law. The line joining planet and sun sweeps out equal area in equal interval of time.
⇒ Kepler’s third law. Cube of mean distance ‘r’ of the planet from the sun is proportional to the square of its orbital period.
TEXTBOOK QUESTIONS (SOLVED)
Q. 1. State the universal law of gravitation.
Ans.— Newton’s universal law of gravitation. This law states that every object in the universe attracts every other object with a force which is proportional to the product of their masses and inversely proportional to the square of the distance between them.
This force always acts along the line joining their centres.
If m₁ and m₂ are the masses of two objects lying distance d apart, then force F between them is :
F = Gm₁ m₂ / d2
where G is a constant, called universal gravitational constant.
Q. 2. Write the formula to find the magnitude of gravitational force between the earth and an object on the surface of the earth.
Ans.— Let ‘m’ be the mass of object on the earth and the mass of earth be ‘M’. If ‘R’ is the radius of the earth, then the formula for gravitational force between earth and object is :
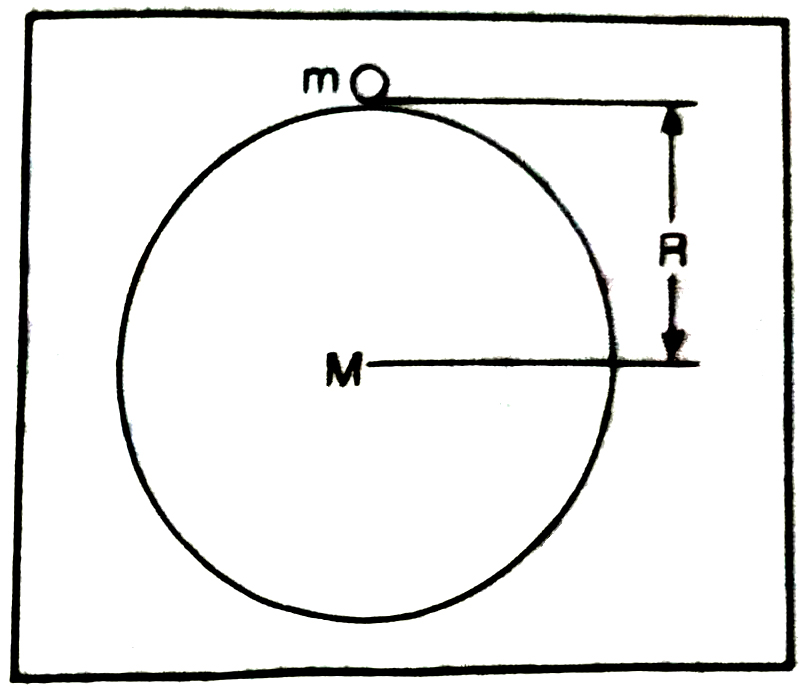
F = GmM / R2
Since the size of the object is very small as compared to that of the earth, therefore distance between centre of object and centre of the earth is taken to be equal to radius of the earth.
Q. 3. What is meant by free fall ?
Ans.— Free Fall. An object is said to be in a state of free fall when it falls towards the earth under the influence of gravitational force between the object and the earth. There is no change in the direction of motion of the body but value of velocity keeps changing due to attraction of earth. It falls towards earth with an acceleration of 9.8 m s -².
Q. 4. What is meant by acceleration due to gravity ?
Ans.— Acceleration due to gravity. The acceleration produced in the motion of a body falling under the force of gravity is called acceleration due to gravity. It is denoted by ‘g’.
Q. 5. What is the difference between the mass of an object and its weight ?
Ans.— Difference between mass and weight :
| Mass | Weight |
| Mass of the quantity of matter contained in a body and is the measure of its inertia. | Weight of a body is the force with which a body is attracted towards the centre of the earth. |
| Mass of a body remains constant at all places. | Weight of a body (W = mg) changes from place to place due to the change in the value of acceleration due to gravity ‘g’. |
| Mass is a scalar quantity. | Weight is a vector quantity. |
| Mass is measured by a pan balance. | Weight of a body is measured by a spring balance. |
| Mass of a body is never zero. | Weight of a body is zero at the centre of the earth. |
| The unit of mass is kg. |
The unit of weight is newton or kg-wt.
|
Q. 6. Why is the weight of the object on moon 1/6 th of its weight on the earth ?
Ans.— We know that, Mass of earth (Me) = 100 × Mass of moon (Mm)
Radius of earth (Re) = 4 × Radius of moon (Rm)
Since the mass and radius of moon is less than that of the earth therefore, moon exerts
lesser {1/6 th) force of attraction on the object. Hence the weight of the object on moon is 1/6 th of the weight of the same object on earth.
TEXTBOOK EXERCISES (SOLVED)
Q. 1. How does the force of gravitation between two objects change when the distance between them is reduced to half ?
Ans.— Let m₁ and m₂ be the masses of the two objects A and B respectively and ‘r’ be m2 the distance between their centres. Therefore, according to the law of Gravitation, the force of attraction between them is given ahead :
F = Gm₁ x m₂ / r2
If the distance between the two objects be reduced to half, then
∴ Force of gravitation between them will be

Using equation (i))
F = 4 × F
Therefore force of attraction will become four times when the distance between the two objects is reduced to half.
Q. 2. Gravitational force acts on all objects in proportion to their masses. Why then, a heavy object does not fall faster than a light object ?
Sol.— Suppose F is the gravitational force that acts on an object of mass ‘m’.
∴ F = G. Mm / r2
and F = mg
From (i) and (ii)
F = GMm / r2 = mg
It is clear that F ∝ m but acceleration due to gravity ‘g’ does not depend upon mass ‘m’. Hence all objects (light or heavy) fall with the same speed when there is no air resistance.
Q. 3. What is magnitude of gravitational force between the earth and a 1 kg object on its surface ? Take mass of earth to be 6 x 1024 kg and radius of the earth is 6.4 x 106 m. G = 6.67 × 10-11 Nm² kg-2.
Sol.— Here Mass of the object (m) = 1 kg
Mass of earth (M) = 6 × 1024 kg
Radius of the earth (R) = 6.4 × 106 m
The magnitude of force of gravitation between object of mass 1 kg and the earth

= 9.77 N
= 9.8 N (Approx) Ans.
Q. 4. The earth and the moon are attracted to each other by gravitational force. Does the earth attracts the moon with a force that is greater than or smaller than or the same as the force with which the moon attracts the earth ? Why ?
Ans.— The earth attracts the moon with the same force as the force with which the moon attracts the earth. According to Newton’s third law, these two forces are equal and opposite.
Q. 5. If the moon attracts the earth, why does the earth not move towards the moon ?
Ans.—According to Newton’s third law, the moon also attracts earth with a force equal to that with which the earth attracts the moon. But the earth is much larger than the moon. So, the acceleration produced in the earth (a ∝ 1/m) is very less and is not noticeable.
Q. 6. What happens to the force between two objects, if
(i) the mass of one object is doubled ?
(ii) the distance between the objects is doubled and tripled ?
(iii) the masses of both objects are doubled ?
Ans.— Force of gravitation, F = G – m₁ m₂ / r2
(i) When mass of one body (m₁ or m₂) is doubled, the force gets doubled.
F = G(2m₁) m₂ / r2
= 2G m₁ m₂ / r2
= 2F
(ii) When distance between the bodies is doubled,

i.e., the force becomes one fourth of the original force.
Q. 7. What is the importance of universal law of gravitation ?
Ans.— Importance of universal law of gravitation :
(i) The gravitational force between the sun and the earth makes the earth move around the sun with a uniform speed.
(ii) The gravitational force between the earth and the moon makes the moon move around the earth with uniform speed.
(iii) The high and low tides are formed in sea due to the gravitational pull exerted by the sun and the moon on the surface of water.
(iv) It is the gravitational pull of the earth, which holds our atmosphere in place.
(v) The gravitational pull of earth keeps us and other bodies firmly on the ground.
Q. 8. What is the acceleration of free fall ?
Ans.— Acceleration of free fall. It is the acceleration produced when a body falls under the influence of the force of gravitation of the earth alone. Near the surface of the earth, its value is 9.8 m s -2.
Q. 9. What do we call the gravitational force between the earth and an object ?
Ans.— The gravitational force between the earth and an object is called weight of the object.
Q. 10. Amit buys few grams of gold at poles as per the instruction of one of his friends. He hands over the same when he meets him at the equator. Will the friend agree with the weight of gold bought? If not, why ?
[Hint : The value of g is greater at the poles than at the equator.]

Ans.— The value of g at the equator is less than that at the poles. Hence, the few gm of gold at poles will measure less when taken to the equator. Therefore, the friend will not agree with the weight of the gold bought.
Q. 11. Why will a sheet of paper fall slower than one that is crumpled into a ball ?
Ans.— The sheet of paper will experience a larger air resistance due to its large surface area than that of its ball from.
Increased force of friction will reduce the forward driving force due to gravity. Hence sheet of paper falls slower than one that is crumbled into a ball.
Q. 12. Gravitational force on the surface of moon is 1/6th as strong as gravitational force on the earth. What is the weight in newton of a 10 kg object on moon and on the earth ?
Sol.— Mass of the object on moon = 10 kg
Mass of the object on the earth = 10 kg
Acceleration due to gravity on the earth (g) = 9.8 m s -2
Weight of the object on the earth (W) = m × g
= 10 × 9.8
= 98 N Ans.
Now weight of the object on moon’s surface = 1/6 × weight of the object on earth 6
= 1/6 × 98 N
= 16.3 N Ans.
Q. 13. A ball is thrown vertically upwards with a velocity of 49 m s –¹. Calculate :
(i) The maximum height to which it rises
(ii) The total time it takes to return to the surface of earth.
Sol.—

Q. 14. A stone is released from the top of a tower of height 19.6 m. Calculate the final velocity just before touching the ground.
Sol.— Here, the height of the tower, (h) = 19.6 m
Initial velocity of stone, (u) = 0
Acceleration due to gravity, (g) = + 9.8 m s –¹
Final velocity of the stone, (v) = ?
Using equation of motion, v2 – u2 = 2gh
v2 – (0)2 = 2 × 9.8 × 19.6
v2 = 19.6 × 19.6
v = √19.6 × 19.6
= 19.6 m s –¹ Ans.
Q. 15. A stone is allowed to fall from the top of the tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m s –¹. Calculate when and where the two stones will meet ? (g = 10 m s-²2)
Sol.— Height of the tower = 100 m
Suppose a stone is allowed to fall from point A at the top of tower and another stone is projected vertically upward from point C. These two stones meet at point B after ‘t’ seconds.
Distance covered by first stone (AB) = x
∴ Distance covered by second stone (CB) = (100 – x)
Downward Journey of first stone
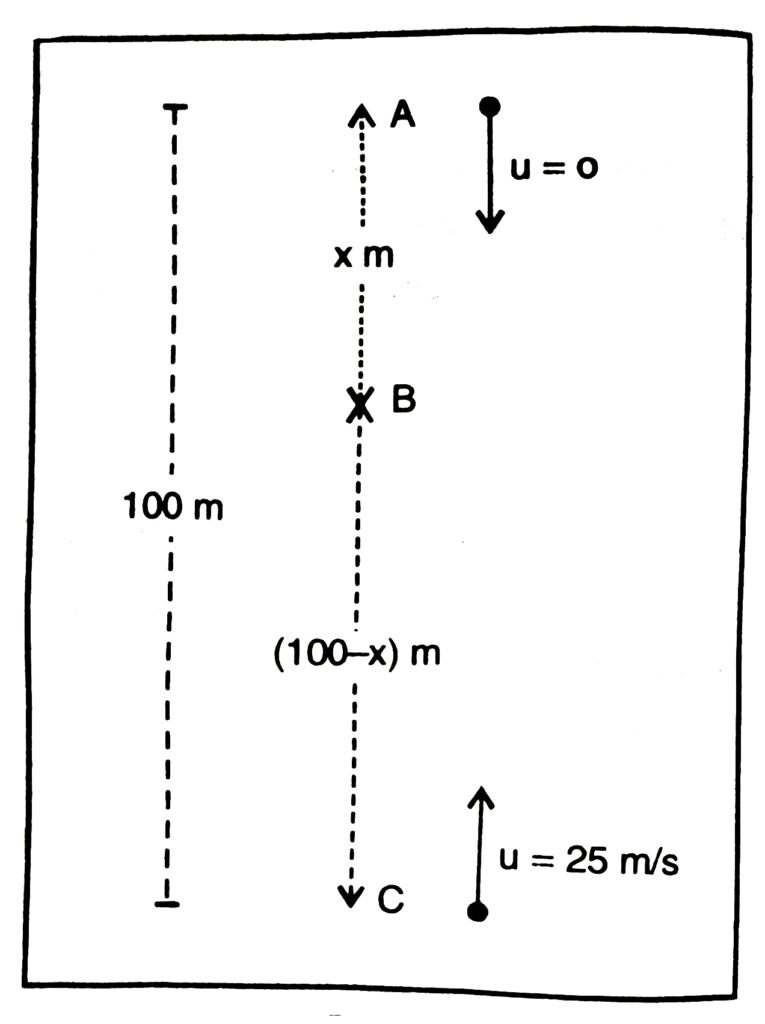


i.e the first stone will cover a distance of 80 m in the downward direction. and second stone will cover upward distance = 100 – x
= 100 – 80
= 20 m Ans.
ADDITIONAL IMPORTANT QUESTIONS
LONG ANSWER TYPE QUESTIONS
Q. 1. Define Newton’s universal law of gravitation and establish mathematical formula for force of attraction between two objects.
Ans.— Newton’s universal law of gravitation— Every particle in this universe attracts each and every particle, the force of attraction is
(i) directly proportional to the product of both the masses and.
(ii) Inversely proportional of the square of the distance between the two. This force always acts along the line joining the two masses.
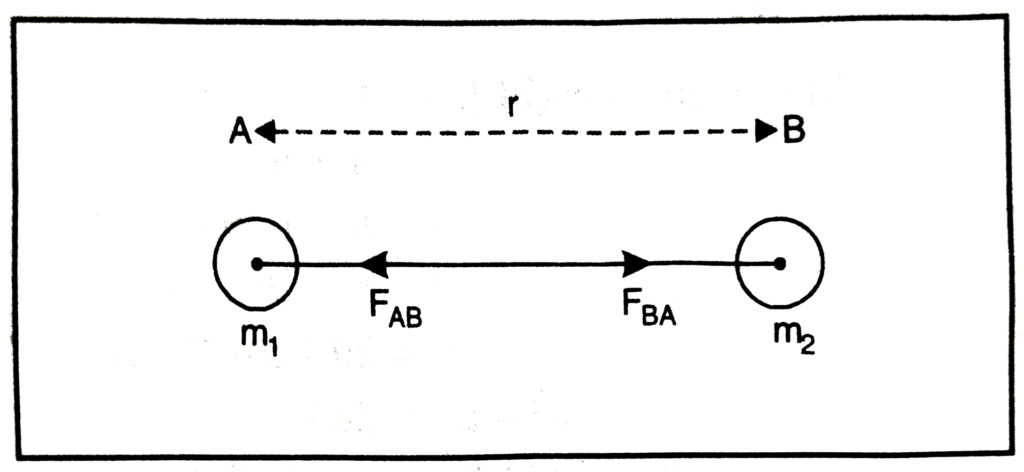
Derivation of Mathematical Formula. From the fig. let there are two balls A and B having masses m₁ and m₂ distance between them is ‘r’.
According to Newton’s third law of motion ball A exerts a force FRBA on the ball B and ball B exerts a force FAB on the ball A. These forces are equal and opposite
FAB = – FBA
Let, FAB = – FBA
then according to law of gravitation
F ∝ m1m2 ….(i)
and F ∝ 1/r² ….(ii)
from (i) and (ii)
F ∝ m1 × m2 / r²
or, F = G m1 × m2 / r²
Where G is universal gravitational constant. This is named so since its numerical value remains constant in whole of the universe and the formula is known as Newton’s universal law of gravitation.
Value of G
G = 6.67 × 10 10–11 Nm2 / kg2
Q. 2. Write Kepler’s law in context with the motion of planets. .
Ans.— By the 16th centuary, a lot of data on the motion of planets had been collected by many astronomers. Johannes Kepler derived three laws based on these data. These are known as Kepler’s laws. These are—
1. Law of orbits (First laws)—The orbit of a planet is an ellipse and the sun is at one of the foci, as shown in fig. In this fig. Sun is shown at O.
2. Law of area (Second laws)— The line joining the planet and sun sweep equal areas in equal intervals of time. Thus, time taken for the motion from A to B is same as for the motion from C to D and area – OAB and OCD are equal.

3. Law of time period (Third law)— The cube of mean distance of a planet from the sun is directly proportional to square of its orbital time period
T2 ∝ r3
But Kepler could not give a theory which explained the motion of planets.
Newton showed that due to motion of planets sun exerts force of gravtation on them. i.e.
r3 / T2 = constant.
Q. 3. How did Robert proved experimentally that all bodies fall in vacuum with same acceleration?
Or
How did Robert Boyle show experimentally that a coin and a piece of paper when dropped simultaneously from same height in vacuum fall with same acceleration.
Ans.— Boyle’s Experiment. As shown in fig. Robert Boyle took a long glass tube. A heavy coin and a piece of paper were placed inside the tube. The ends of the tube were closed. Air from the tube was removed with the help of a vacuum pump. When the tube was quickly inverted it was seen that coin and a piece of paper hit the bottom of the tube at the same time. Now the experiment was repeated with air inside the glass tube.

This time it was observed that a piece of paper falls slowly whereas the coin immediately hit the bottom of glass tube. This experiment proves that in vacuum all bodies irrespective of their masses (both light and heavy) fall towards earth with same acceleration
Q. 4. (a) Prove that acceleration due to gravity is independent of mass. (b) Find the value of ‘g’.
Ans.— (a) Consider a body of mass ‘m’ lying on the surface of earth. Suppose M are respectively mass and radius of earth.
Let F be the force of gravity acting on the body

This acceleration is called acceleration due to gravity
∴ g = Gm / R2
This equation is free from mass ‘m’ . This shows that due to force of gravity the acceleration produced in an object is independent of its mass.
(b) To find the value of ‘g’


Q. 5. Describe those factors which are responsible for variation in the value of acceleration due to gravity ‘g’ ?
Ans.— Variation in the value of acceleration due to following factors : Variation in g with altitude-Value of ‘g’ is maximum on the surface of earth. As we move in upward direction (higher altitudes) value of ‘g’ goes on decreasing. We can calculate value of ‘g’ at altitude using a mathematical formula. If
ge = acceleration due to gravity on the surface of earth
gh = acceleration due to gravity at height h
R = radius of earth
we know

(ii) Variation in g due to shape of earth—
Earth is not exactly spherical. It is some what egg shaped. Its radius at than that at equator as shown in fig.

As shown in fig. radius of earth at equator is 6378 km and radius of earth at poles is 6357 km. Thus, value of gp at poles is gp = 9.831m s –² (maximum) and minimum value at equator is g = 9.782 m s-2. We use average value of g calculated from ge and gp .
(iii) Effect of depth— If we go deep under the earth e.g. in caves or in mines, value of ‘g’ is decreased value of g goes on decreasing, if depth goes on increasing. At the centre of earth, value of g is zero.
Wd / We = gd / ge = [1 – d/R]
Q. 6. Establish the relation between ‘g’ and ‘G’.
Or
Deduce an expression for it in terms of mass of the earth ‘M’ and universal gravitational constant ‘G’.
Or
Show that the acceleration due to gravity of an object is independent of its mass.
Ans.— Relation between ‘g’ and ‘G’. Suppose the earth is a sphere of mass M and radius R, Consider a body of mass m lying at a distance ‘r’ from the centre of the earth. According to Newton’s law of gravitation, the force of attraction between the earth and the body,
F = GMm / r2 …(i)
This force of gravity produces an acceleration ‘g’, is the body of mass m.
Hence, from Newton’s second law,
F = Mass × Acceleration
F = m × g ….(ii)
From equations (i) and (ii) we get
mg = GMm / r2
or, g = GM / r2 ….(iii)
This equation gives relation between acceleration due to gravity ‘g’ at points far away from the earth and gravitational constant ‘G’.
Since (iii) does not involve ‘m’ it is therefore evident that ‘g’ does not depend upon the mass of the body.
SHORT ANSWER TYPE QUESTIONS
Q. 1. Which one is greater-the gravitational force of the earth on 1 kg iron or the force of gravitation applied by 1 kg on earth ?
Ans.— According to Newton’s law of Gravitation there exists of mutual force of attraction between two objects. Therefore, neither the earth applies force on iron nor iron on earth. Since the mass of iron is less than the mass of the earth, therefore earth attracts 1 kg mass towards it with a greater force which is noticeable.
Q. 2. Why is G called universal gravitational constant ?
Ans.— G is called universal gravitational constant because its numerical value is same in the whole universe. This value is G = 6.67 x 10-11 Nm²/ kg².
Q. 3. Is the value of ‘g’ at a given place same for different bodies or it is variable ?
Ans. From the relation between the acceleration due to gravity ‘g’ and universal gravitational constant G, we know
g = GM / r2
From this From this equation it is evident that the value of ‘g’ does not depend upon the mass of the body. Thus we reach a conclusion that at a given place the value of g is same for different bodies.
Q. 4. Why does a body becomes weightless at the centre of earth ?
Ans.— We know value of g goes on decreasing as we continue moving deep into the earth and value of acceleration due to gravity (g) = 0 at the centre of earth. Thus, a body whose mass is m,
Weight of body = m × 0 = 0
Therefore, body becomes weightless.
Q. 5. A tennis ball jumps higher at hills than at planes. Explain.
Ans.— Value of g decreases with altitude, thus gravitational force acting on ball at hills is less as a result ball jumps higher at hills than at planes.
Q. 6. The weight of an object on the surface of earth is 9.8 N. What does this statement mean ?
Ans.— We know that value of ‘g’ on the surface of earth is 9.8 m/s² and the relation for weight of an object is :
w = m × g
9.8 = m × 9.8
or, m = 9.8 / 9.8
∴ m = 1 kg
The given statement therefore means the mass of the object on earth is 1 kg.
Q. 7. What type of motion a freely falling body execute under gravity ?
Ans.—A body falling freely under gravity executes uniform accelerated motion. If bodies with different masses and different shapes are allowed to fall freely in vacuum, they all will have same acceleration due to gravity.
Q. 8. Give points of difference between Acceleration due to gravity (g) and Universal gravitational constant (G).
Ans.— Difference between g and G :
| Acceteration due to gravity (g) | Gravitational constant (G). |
| It represents acceleration acquired by the body due to on insiero fois gravity. | It represents force of attraction between two masses of 1 kg each lying 1 m apart. |
| Its value is different at different places on earth surface. | Its value is constant at all places. Thus, it is called universal constant. |
| Its value at the surface of earth 900 is 9.8 m/s². | Its value is 9.67 x 10-11 Nm²kg-². |
| It is a vector quantity. | It is a scalar quantity. |
Q. 9. You buy W weight of sugar at a place situated on equitorial line and then take it to Antarctica. Will that sugar weigh same there? If not whether it would be more or less.
Ans.— The value of ‘g’ at Antarctica is not same as on equator. The value of ‘g’ increases on Antarctica therefore, sugar bought at any place on equitorial line when taken to Antarctica would have more weight but its mass will remain the same because mass is a constant quantity.
Q. 10. Why cannot we move a finger without disturbing all the stars ?
Ans.— When we move our finger, then distance between finger and all other things in the universe change and as a result force of gravitation also changes. Thus, all the things get disturbed, although this disturbance is negligible.
Q. 11. Distinguish between Gravitation and Gravity.
Ans.— Gravitation. Gravitation is the force of attraction between any two bodies in the universe. The attraction between the sun and the earth, the attraction between a table and a chair are examples of gravitation.
Gravity. Gravity is a special case of gravitation when one of the two bodies is the earth. Gravity is the attraction between the earth and any object lying on or near its surface. A ball thrown upward falls back on the surface of the earth due to earth’s force of gravity.
Q. 12. Explain why a small piece of stone is not attracted towards another big piece of stone on the earth’s surface ?
Ans.— Because of very small value of G, the force of attraction between any two such ordinary sized bodies is so small that it cannot produce motion in them.
Q. 13. The earth attracts an apple. Does the apple also attract with earth ? If it does, why does the earth not move towards the apple ?
Ans.— The apple also attracts the earth with an equal and opposite force. The mass of the earth is very large compared to that of apple. So, the acceleration produced in earth is very small as compared to that in the apple. Hence, the motion of the earth towards the apple is not appreciable and therefore, is not noticeable.
Q. 14. If the force of gravity somehow vanishes today, why would we be sent being in space ?
Ans.— In the absence of force of gravity, the centripetal force required to keep us rotating along the earth would not be available. As a result would fly off along the tangent to with into the space.
NUMERICAL PROBLEMS (SOLVED)
Q. 1. Two spheres of 1 kg mass each are separated by 3m. Calculate the gravitational force between then. Given G = 6.67 × 10-11 Nm2 / kg2.
Sol.— Here m1 = m2 = 1 kg
Distance between two spheres, (r) = 3 m
Gravitational constant (G) = 6.67 × 10-11 Nm2 / kg2
We know, F = G. m1 × m2 / r2
F = 6.67 × 10-11 × 1 × 1 / (3)2
= 6.67 × 10-11 × 1 × 1 N / 9
= 0.741 × 10-11 N
∴ F = 7.41 × 10-12N (Approx) Ans.
Q. 2. The radius of moon is 1.7 × 106 m and mass is 7.35 × 1022 kg. What is the acceleration due to gravity on the surface of moon ? Given G = 6.67 × 10-11 Nm2 / kg2
Sol.— Radius of moon, (R) = 1.7 × 106 m
Mass of moon, (M) = 7.35 × 1022 kg
Gravitational constant, (G) = 6.67 × 10-11 Nm2 / kg2 (Given)
We know, acceleration due to gravity on moon
g = GM / R2

Q.3. Find the change in weight percentage of a body when it is taken from equator to peoples. Polar radius is 6357 km and equtitorial radius is 6378 km.
Sol.— Polar radius, (r) = 6357 km
Equitorial radius, (R) = 6378 km

Q. 4. At what height above the earth surface, the acceleration due to gravity will be half that on the surface of earth ? Suppose R is the redius of earth.
Sol.— Let h be the height above earth surface where

∴ h = 0.414 R Ans.
Q. 5. A stone dropped from the edge of a roof top. If it crosses 2 m high window in 0.1 second then what is the distance between the upper end of window and the roof ?

Sol.— Distance covered in crossing the window
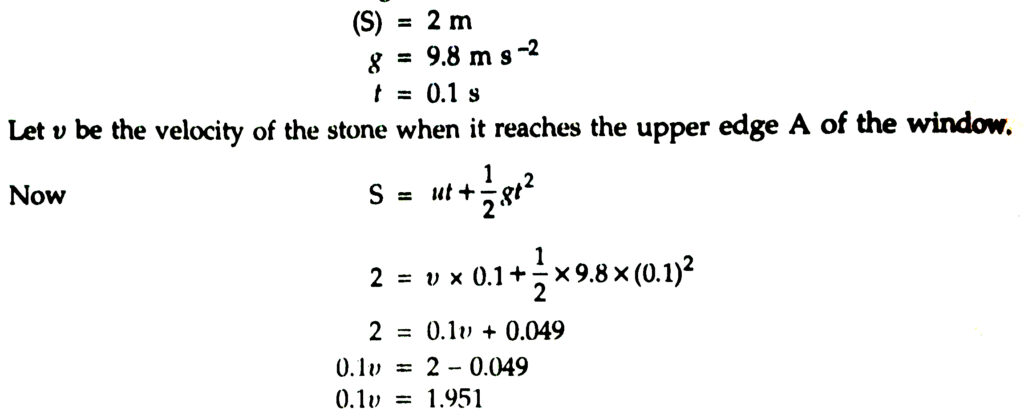

VERY SHORT ANSWER TYPE QUESTIONS
Q. 1. What is g on the moon as compared to that on earth ?
Ans.— Nearly 1/6 th of its value on earth.
Q. 2. What is unit of G ?
Ans.— It is Nm² kg -².
Q. 3. What is the mass of the earth ?
Ans.— It is about 6 × 1024 kg.
Q. 4. What is essential property of matter-mass or weight ?
Ans.— Mass is the basic and essential property. It is constant everywhere. Weight of a body varies from place to place.
Q. 5. What is SI unit of weight of a body ?
Ans.— It is newton (N).
Q. 6. The earth’s gravitational force causes an acceleration of 5 m s-2on a 1 kg mass somewhere in the space. How much will be the acceleration of a 3 kg mass at that place ?
Ans.— Same i.e., 5 m s-2 since g at a place is independent of mass of the body.
Q. 7. Why one can jump higher on the surface of moon than on the earth ?
Ans.—The g at moon surface is nearly 1/6th of that at the surface of earth. Hence can jump six times higher on the moon with a given initial velocity.
Q. 8. Give the value of universal gravitational constant in S.I. units. one
Ans.— (G) = 6.67 x 10-11 Nm²/kg²
The value of gravitational constant.
Q. 9. The value of ‘G’ on the surface of earth is 6.67 x 10-11 Nm²/kg². What is its value on the surface of moon ?
Ans.— Since G is universal constant so its value on moon surface will be same as on the earth surface i.e. G = 6.67 × 110-11 Nm²/kg².
Q. 10. State two factors on which the gravitational force between two objects depends.
Ans.— The gravitational force between two objects depends on : (i) their masses (ii) distance between them.
Q. 11. Write the formula to find the magnitude of gravitational force between the earth and an object on the surface of the earth.
Ans.— F = G Mm / r2
Q. 12. Can the mass of a body be zero.
Ans.—No, mass of body can never be zero.
Q. 13. The weight of an object on the moon is ………………. its weight on the earth.
Ans.— The weight of an object on the moon is 1/6th its weight on the earth.
Q. 14. You find your mass to be 42 kg on a weighing machine. Is your ma mass less than 42 kg ?
Ans.— Mass is a constant quantity. So, it can not be more or less than 42 kg.
Q. 15. How does the vary from equator to poles ?
Ans.—The value of ‘g’ increases as we move from equator to poles.
Q. 16. What will be the weight of an object on the earth whose mass is 10 kg ?
Ans.— Weight of the object on earth
(W) = m × g
= 10 kg × 10 m s -²
= 100 N
Q. 17. Write the S.I. unit of G.
Ans.— Nm²/kg².
Q. 18. Fill in the blank:
The weight of an object on the moon is …………. its weight on the earth.
Ans.— 1/6th.
MULTIPLE CHOICE QUESTIONS
Select the correct answer :
1. Mass of body on moon is :
(A) same as that on the earth
(B) 1/6th of that at the surface of the earth
(C) 6 times as that on the earth
(D) none of these.
Ans.— (A) same as that on the earth
2. In vacuum all the freely falling objects have same :
(A) speed
(B) velocity
(C) acceleration
(D) force.
Ans.— (C) acceleration
3. When an object is thrown up, the force of gravity :
(A) is opposite to the direction of motion
(B) is in the same direction as direction of motion s
(C) decreases as it rises up
(D) increases as it rises up.
Ans.— (A) is opposite to the direction of motion
4. The force of gravitation between two bodies does not depend on :
(A) their separation
(B) the product of their masses
(C) the sum of their masses
(D) the gravitation constant.
Ans.— (C) the sum of their masses
5. The acceleration due to gravity :
(A) has the same value everywhere in the space
(B) has the same value everywhere on the earth
(C) varies with lititude on the earth
(D) is greater on the moon due to its smaller diameter.
Ans.— (C) varies with lititude on the earth
6. A person weighs W at Delhi. The weight of the person on the peak of Mount Everest will be :
(A) = W
(B) < W
(C) > W
(D) zero.
Ans.— (B) < W
7. Gravitational force (F) between earth of mass M and on object of mass m lying on the surface of the earth (radius of earth = R) is :
(A) GM/mR²
(B) GMm/R²
(C) GMn/R
(D) GMmR²
Ans.— (B) GMm/R²
8. Gravity is the force of attraction between :
(A) the sun and the moon
(B) the moon and the satellite
(C) the earth and an object
(D) the sun and jupiter.
Ans.— (C) the earth and an object
9. The gravitational force between two bodies varies with distance r as :
(A) 1/r
(B) 1/r²
(C) r
(D) r²
Ans.— (B) 1/r²
10. The value of G is :
(A) 9.8 m s -²
(B) 9.8 × 10-11 Nm² kg-²
(C) 6.773 × 10-11 Nm² kg-²
(D) 6.773 × 10-11 Nm² kg-²
Ans.— (C) 6.773 × 10-11 Nm² kg-²
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here