WBBSE 10th Class Science Solutions Physical Science & Environment Chapter 2 Behaviour of Gases
WBBSE 10th Class Science Solutions Physical Science & Environment Chapter 2 Behaviour of Gases
West Bengal Board 10th Class Science Solutions Physical Science & Environment Chapter 2 Behaviour of Gases
WBBSE 10th Class Physical Science & Environment Solutions
Synopsis
Boyle’s Law and Charles’ Law
- Pressure of a gas is defined as the normal force exerted by the gas molecules on unit area of the wall of the container (in which the gas is kept).
- Units of pressure in CGS system and Sl are dyn/cm² and N/m², respectively. N/m² is also called Pa (pascal). 1 Pa = 10 dyn/cm²
- Dimensional formula of pressure is ML-1T-2 .
- The volume of a gaseous substance means the volume of the container in which it is kept.
- Unit of volume in SI is m³ and in CGS system is cm³. One practical unit of volume is litre (L).
1 m³ = 1000 L, 1 L = 1000 cm³,1 m³ = 106 cm³
- Dimensional formula of volume is L³.
- Manometer is used to measure pressure of a gas or air. This is also called pressure gauge.
- The pressure exerted by a 76 cm of mercury at 0°C at sea level at latitude of 45° is called the standard atmospheric pressure or normal atmospheric pressure (atm).
1 atm = 1.013 × 106 dyn/cm²Two other units of pressure are bar and torr.1 bar = 106 dyn/cm²and 1 torr = pressure exerted by 1 mm long mercury column= 1332.8 dyn/cm²
TOPIC – A
Boyle’s Law and Charles’ Law
SHORT AND LONG ANSWER TYPE QUESTIONS
Q.1 Explain the pressure of a gas on the basis of molecular motion and collision of gas molecules with the walls of the vessel.
Ans. The force of attraction amongst the molecules of a gaseous material is negligible. So the gas molecules are always moving randomly. The molecules always collide amongst themselves and also with the walls of the vessel and undergo change of momentum. The rate of change of momentum is force, i.e., the wall exerts force on the molecules. In reaction to the force exerted by the walls, gas molecules also exert force on the walls. This force per unit area acting perpendicularly on the wall of the vessel is the pressure of the gas.

Q. 2 Define pressure of a gas. What are the units of pressure in CGS system and SI? Establish a relation between these two units.
Ans. Pressure of a gas is the force per unit area exerted by the gas molecules on the walls of the vessel.
Units of pressure in CGS system and Sl are dyn/ cm² and N/m², respectively.
The relation between the units is
Q. 3 What is the volume of a gas? What are the units of volume in CGS system and SI?
Ans. The volume of a gas is the volume of the container in which it is kept.
The units of volume in CGS system is cm³ or ml and in Sl is m³.
Q.4 The height of the mercury column is h1 in the open-end arm of the manométer U-tube and it is h₂ in the other arm of the U-tube. Compare the pressure of enclosed gas in the manometer with the atmospheric when pressure: (1) when h₁> h₂, (2) h₁< h₂, (3) when h₁ = h₂.
Ans. (1) When h₁> h₂, it is understood that the pressure of the enclosed gas is more than the atmospheric pressure. If the pressure of the enclosed gas is and the atmospheric p1 pressure of that place is p0, then
p₁ = p0 + pressure of a mercury column of height (h₁-h₂)
∴ p₁ = p0 + (h₁-h₂) dg
where density of mercury is d and acceleration due to gravity at that place is g.

(2) If h₁ < h₂, it is understood that the pressure of the enclosed gas is less than atmospheric

pressure. If the pressure of the enclosed gas is p2 , then p2 = p0 – (h₂ – h₁)dg.
(3) If h₁ = h₂, it is understood that the pressure of the enclosed gas inside the manometer is equal to the atmospheric pressure. In this case, if the pressure of the enclosed gas p3, then p3 = p0.
Q. 5 By taking some amount of air on the top of the mercury column in a defective barometer, determine the pressure of the atmosphere.
Ans. Let us assume, the height of mercury in this defective barometer is H₁ cm and the height of air column above the mercury column is x₁ cm. If the area of cross section inside the tube is A cm², then the volume of air, V₁ = x₁A cm³. If the atmospheric pressure is equal to the height of a mercury column of H cm, the pressure of this V₁ volume of air,
p₁ = pressure of (H-H₁) cm of mercury column. Now the open end of the barometer immersed in mercury is raised a little upward. If the height of mercury in the tube is H₂ and the height of air column above the mercury column is x₂ cm then the volume of enclosed air, V₂ = x₂A cm³.
Since the mass of enclosed air and temperature remain constant, we get from Boyle’s law,
p1V1 = p2V2
or, (H – H1) · x1A = (H – H2) · x2A

Q.6 Write down Boyle’s law and explain it. Or, State the law which establishes the relation p₁V₁= p₂V2.
Or, Write down the law from which the relation between the volume and the pressure of an ideal gas is known.
Ans. Boyle’s law: At constant temperature, the volume of a fixed mass of a gas is inversely proportional to the pressure of the gas.
Explanation: If V and p are the volume and the pressure of the gas respectively, then according to Boyle’s law,

where K1 is a constant whose value depends on the mass and the temperature of the gas. Therefore, with the temperature of a fixed mass of gas remaining constant, the product of the pressure and the volume of the gas is a constant. Now, if the temperature of a fixed mass of a gas remains constant and V₁, V₂ and V3 are the volumes of the gas at pressures p₁, p2 and p3 respectively, then according to Boyle’s law,
p1V1 = p2V2 = p3V3 = ··· = K₁ (constant)
Q.7 Write down Charles’ law and explain it.
Ans. Charles’ law: At constant pressure, the volume of a given mass of a gas increases or decreases by 1/273 of its volume at 0°C for every 1°C rise or fall in temperature.
Explanation: Let the volume of a given mass of a gas at constant pressure be V0 at 0°C. By keeping the pressure constant, if the temperature of the gas is changed, then according to Charles’ law at 1°C the volume of the gas becomes
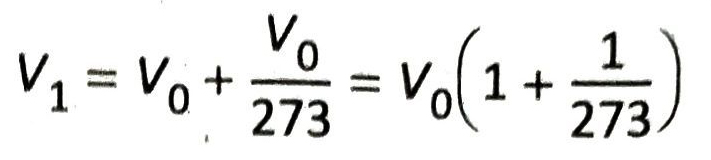
At 2°C, the volume of the gas becomes

In a similar way, at t°C the volume of the gas becomes
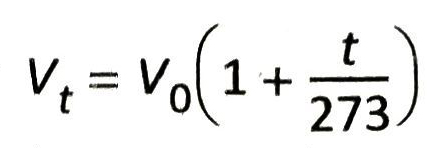
Similarly, keeping the pressure constant, if the temperature is decreased by t°C, the volume of the gas becomes
Q.8 Draw the graph of V-t of Charles’ law and give an idea of absolute zero temperature from it.
Ans. At constant pressure, if a graph of a given mass of gas is drawn by taking temperature (t) as abscissa and volume (V) at that temperature as ordinate, then the curve obtained is a straight line [Fig.].

If the straight line is extended backward, it cuts the temperature axis at -273°C. This means that at constant pressure, the volume of a gas becomes zero at -273°C. This temperature is called the absolute zero temperature.
Q.9 Write Charles’ law according to the absolute scale of temperature.
Ans. If the volume of any gas of a given mass is Vo at 0°C temperature, then according to Charles’ law, the volume of the gas at constant pressure and t₁°C becomes

where T₁ is the reading of t₁°C temperature in absolute scale.
Similarly, volume of the same gas at constant pressure and t₂°C becomes

where T₂ is the reading of t₂°C temperature in absolute scale.
Now, adding equations (1) and (2), we get

So, at constant pressure, the volume of a given mass of gas is directly proportional to the absolute temperature of the gas.
This is an alternative form of Charles’ law.
Q.10 Why is the term m ‘fixed mass of a gas’ mentioned while stating Boyle’s law?
Ans. The term ‘fixed mass of a gas’ is always mentioned at the time of stating Boyle’s law because pressure and volume of the gas depend on mass. If the mass is changed, pressure and volume also get changed.
Q.11 Establish a relation between m³ and L.
Ans. 1L = 10³ cm³
∴ 1m³ = 106 cm³ = 10³. 10³ cm³ = 10³ L
Q.12 Draw the p-V curve according to cording to Boyle’s law.
Ans. At constant temperature, the volume (V) and the pressure (p) of a fixed mass of gas are plotted. Here, Vis plotted along the abscissa and p is plotted along the ordinate. The graph is shown in Fig. 10. This is the p-V graph of Boyle’s law. The nature of the curve in the graph is rectangular hyperbola.
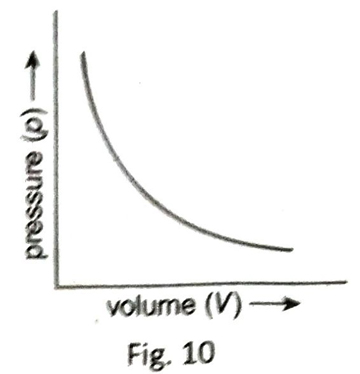
Q.13 Draw the pV-p curve according to Boyle’s law.
Ans. In Fig. 11, we find a curve where the pressure p of a gas of fixed mass under constant temperature is plotted along the abscissa and the product (pV) of the pressure and the volume is plotted along the ordinate. This is the (pV-p) curve of Boyle’s law. Its nature is straight line and it is parallel to the pressure axis.

Q.14 In the case of a real gas, how does the total volume of the molecules of the gas influence Boyle’s law?
Ans. In case of real gases, we cannot neglect the volume of the gas molecules and hence, pressure can be increased only up to a definite level at a certain temperature. For this reason, Boyle’s law cannot be accurately applied at any temperature.
Q.15 When a balloon is inflated, both its pressure and volume increase, Is Boyle’s law violated here?
Ans. When the balloon is inflated, the mass of air inside the balloon does not remain constant. When air is pumped into the balloon, the mass of air inside it increases. We know that there are two constants in Boyle’s law-mass of the gas and its temperature. As the mass of air does not remain constant, so Boyle’s law is not applicable here. Hence, there is no question of its violation.

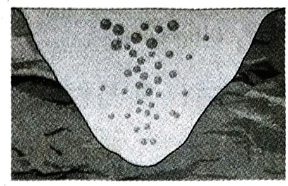
Q.16 Why does the volume of an air bubble increase when it goes up from deep inside a water body?
Ans. Pressure of water increases as one goes deeper inside a water body. So, when air bubble comes upward from the depth of a water body, the pressure of water on it decreases gradually. Now suppose the temperature of water is uniform everywhere. Thus, according to Boyle’s law, when an air bubble comes upward from the depth, its volume is inversely proportional to the pressure of water, i.e., volume increases as pressure decreases.
Q.17 What is absolute scale of temperature?
Ans. Physicist Lord Kelvin introduced a new scale for measurement of temperature whose zero point is taken as -273°C and the value of each degree is taken to be equal to one degree of Celsius scale. In SI, a temperature of 0.01°C is considered as 273.16 K in this scale. This scale is called the absolute scale of temperature.
VERY SHORT ANSWER TYPE QUESTIONS
Choose the correct answer
1. In Boyle’s law,
A. only mass of the gas remains constant
B. only temperature of the gas remains constant
C. mass and pressure of the gas remain constant
D. mass and temperature of the gas remain constant
Ans. D
2. The volume (V) of a definite mass of an ideal gas is plotted against its temperature (t°C) at a constant pressure. What is the temperature at which the curve intersects the temperature axis?
A. 0°C
B. –136.5°C
C. –273°C
D. 273°C
Ans. C
3. In which scale of temperature, it is not possible for the value of temperature to be negative?
A. Celsius scale
B. Fahrenheit scale
C. absolute scale
D. all of these
Ans. C
4. Pressure and volume of a definite mass of gas are given by p and V, respectively. If pressure is increased by 25% keeping the temperature constant, what is the new volume?
A. 0.6V
B. 0.75V
C. 0.8V
D. 0.85 V
Ans. C
5. 1 Pa = how many dyn/cm²?
A. 1
B. 10
C. 100
D. 1000
Ans. B
6. The nature of p-V curve according to Boyle’s law is
A. straight line
B. circle
C. parabola
D. rectangular hyperbola
Ans. D
7. The nature of pV-p curve according to Boyle’s law is
A. straight line
B. circle
C. rectangular hyperbola
D. none of the above
Ans. A
8. Value of absolute zero in Fahrenheit scale is
A. –452.4°F
B. –462.4°F
C. –459.4°F
D. –463.4°F
Ans. C
9. Unit of pressure in SI is
A. N/m²
B. bar
C. torr
D. dyn/cm²
Ans. A
10. 1m³ = how many cm³ ?
A. 10³
B. 104
C. 105
D. 106
Ans. D
11. 1m³ = how many L?
A. 1
B. 10
C. 100
D. 1000
Ans. D
12. The temperature of a fixed mass of gas is changed from 0°C to 30°C at constant pressure. What is the ratio of its initial and final volume?
A. 91 : 101
B. 91 : 100
C. 91 : 111
D. 91 : 121
Ans. A
13. The temperature of a fixed mass of gas is changed from 0°C to 30°C by heating at constant pressure. How many times is the final volume of the initial volume?
A. 1.2 times
B. 1.5 times
C. 2 times
D. 3 times
Ans. C
14. The volume of a definite mass of gas at room temperature and a pressure of 76 cm of mercury is 1 L. What is its volume at a pressure of 38 cm of mercury if the temperature remains constant?
A. 1.5 L
B. 2 L
C. 3 L
D. 4 L
Ans. B
15. At constant temperature, if the pressure on a definite mass of gas becomes 1/4 of its initial value then the volume increases by
A. 2 times
B. 3 times
C. 4 times
D. 5 times
Ans. B
16. An idle gas at 27°C is heated at constant pressure so as to triple its volume. The temperature of the gas will be
A. 600 K
B. 900°C
C. 627°C
D. 900°F
Ans. C
Answer in brief
1. Which instrument is used to measure pressure of air enclosed in a container?
Ans. Manometer is used to measure the pressure of air enclosed in a container.
2. Pa (pascal) is unit of which physical quantity?
Ans. Pa is the unit of pressure.
3. What is the relationship between Pa and N/m² ?
Ans. 1Pa = 1N/m²
4. While measuring pressure of a gas in a closed container by a manometer, level of mercury is higher in the open-end arm than the other arm. What does it signify?
Ans. It signifies that pressure inside the closed container is greater than the atmospheric pressure.
5. While measuring pressure of a gas in a closed container by a manometer, level of mercury is lower in the open-end arm than the other arm. What does it signify?
Ans. It signifies that pressure inside the closed container is lesser than the atmospheric pressure.
6. Pressure of a gas depends on which factors?
Ans. The pressure of a gas depends on its mass, volume and temperature.
7. At constant pressure, the volume of a certain quantity of a gas depends on which factor?
Ans. The volume of a certain quantity of a gas at constant pressure depends on the temperature of the gas.
8. Mention the constants in Boyle’s law.
Ans. Constants in Boyle’s law are: (1) mass of gas and (2) temperature.
9. Mention constants in Charles’ law.
Ans. Constants in Charles’ law are: (1) mass of gas and (2) pressure of gas.
10. What is the relationship between Celsius scale and absolute scale of temperature?
Ans. If the temperature of a body is t°C in Celsius scale and TK in absolute scale, then T = t + 273.
11. What is absolute temperature?
Ans. Absolute temperature is the temperature of a body according to a scale where zero is taken as absolute zero.
12. What is the value of freezing point of water in absolute scale?
Ans. Freezing point of water in absolute scale is 273 K.
13. What is the boiling point of water in absolute scale?
Ans. Boiling point of water in absolute scale is 373 K.
14. What is the nature of V-t graph according to Charles’ law?
Ans. The V-t graph according to Charles’ law is a straight line intersecting the x-axis at -273 K.
15. What is the nature of V-T graph according to Charles’ law?
Ans. The nature of V-T graph according to Charles’ law is a straight line passing through origin.
16. At which temperature, the V-T curve of Charles’ law intersects the temperature axis?
Ans. The V-T curve of Charles’ law intersects the temperature axis at OK.
17. Is it possible to have a temperature lower than the absolute temperature?
Ans. No, it is not possible to have a temperature lower than the absolute temperature.
18. What would be the volume of an ideal gas at absolute zero temperature?
Ans. Volume of an ideal gas at absolute zero temperature is zero.
19. What is the value of 400K in Celsius scale?
Ans. The value of 400K in Celsius scale = (400-273)°C = 127°C
20. If there is a 273 K change in temperature of a body, what is the corresponding value of this change in Celsius scale?
Ans. A change of 273 K in the temperature of the body results in a change of 273°C in Celsius scale.
21. If the temperature of a body changes from 270 K to 273 K, what is its corresponding increase in Celsius scale?
Ans. Increase in temperature of the body = (273-270)K: = 3 K = 3°C (increase of temperature in Celsius scale)
22. If the temperature of a body changes from 270 K to 273 K, what is the present temperature of the body in Celsius scale?
Ans. The present temperature of the body = 273K = 0°C
23. Does the absolute zero temperature of a gas depend on its nature, mass, volume or pressure?
Ans. No, absolute zero temperature of a gas does not depend on its nature, mass, volume or pressure.
24. At low pressure or high pressure do the real gases the roughly follow equation pV = KT?
Ans. Real gases follow roughly the equation pV = KT at low pressure.
Fill in the blanks
1. The volume of a gas increases if its temperature is increased or pressure is …………
Ans. decreased
2. The volume of a gas decreases if its temperature is decreased or pressure is ………..
Ans. increased
3. …………… developed an air-pump to experimentally verify Boyle’s law.
Ans. Robert Hooke
4. When air bubbles rise up from the bottom surface of deep water, then volume ………….
Ans. increases
5. If the volume of a fixed mass of gas at 0°C temperature is Vo, then its volume at t°C temperature and at constant pressure is …………
Ans. V0(1+t/273)
6. In reality, we …………. get a temperature less than the absolute zero temperature.
Ans. do not
7. …………. , a scientist introduced the concept of absolute scale of temperature.
Ans. Kelvin
8. Among solid, liquid and gaseous, materials, force of attraction between the molecules is highest in ……….
Ans. solid
9. ………… law is the law relating pressure and volume of a gas of fixed mass at constant temperature.
Ans. Boyle’s
10. ……….. law is the law relating volume and temperature of a fixed mass of gas at constant pressure.
Ans. Charles’
11. Due to lack of experimental proof, the complete idea of atoms and molecules during Avogadro’s time was ………
Ans. hypothetical
12. If pressure of an enclosed air is more than the atmospheric pressure, the level of mercury in the open-end arm of a manometer is ………….. than the other arm.
Ans. higher
13. If pressure of an enclosed air is less than the atmospheric pressure, the level of mercury in the open-end arm of a manometer is ………… than the other arm.
Ans. lower
TOPIC – B
Combination of Boyle’s Law and Charles’ Law, Ideal Gas Equation, Avogadro’s Law
SHORT AND LONG ANSWER TYPE QUESTIONS
Q.1 Establish the combined form of Boyle’s combined form of Boyle’s and Charles’ law.
Ans. Suppose, pressure and volume of a fixed mass of any gas at absolute temperature T are p and V, respectively.
According to Boyle’s law, V ∝ 1/p (when mass of gas and T are fixed).
According to Charles’ law, V ∝ T (when mass of gas and p are fixed).
Thus, according to the law of combined variation,

where K is a proportional constant.
Let the initial pressure, volume and absolute temperature of a fixed mass of gas be p₁, V₁, T₁ and final pressure, volume and absolute temperature be p₂, V₂ and T₂ respectively. Then from equation (1), we get
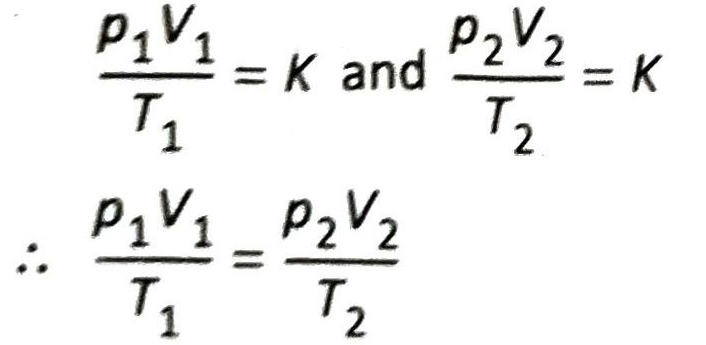
This is the combined form of Boyle’s law and Charles’ law.
Q.2 Under what circumstances, a real gas may behave like an ideal gas?
Or, Give the arguments in favour of considering a real gas as an ideal gas.
Ans. The volume of a definite mass of a real gas increases steadily when the pressure on it is reduced under constant temperature. Again, the volume of a definite mass of a real gas increases steadily when the temperature of it is increased under constant pressure. As the volume of the gas increases, the mutual distance between its molecules also increases. As a result, the value of mutual attractive force between the molecules is also reduced. For an ideal gas, it is assumed that there is no mutual attractive force between the molecules. With these arguments, a real gas behaves like an ideal gas under the lowest possible pressure or the highest possible temperature.
Q. 3 What are the contributions of Avogadro’s hypothesis?
Ans. Contributions of Avogadro’s hypothesis: (1) Atoms and molecules are differentiated for the first time, in Avogadro’s hypothesis. (2) Gay-Lussac’s law of gaseous volume can be explained satisfactorily with the help of Avogadro’s hypothesis. (3) With this hypothesis, correlation can be established between Dalton’s atomic theory and Gay-Lussac’s law of gaseous volume.
Q.4 The molar volumes of real gases at any given temperature and pressure are more or less equal and its limiting value at STP is 22.4 L.mol-¹. From the above experimental facts, deduce Avogadro’s hypothesis.
Ans. Value of molar volume does not depend on the nature of the gaseous material. If the temperature and the pressure remain constant, then the values of molar volumes of different real gases remain nearly equal. If the volume of n mol of a gas is V, then molar volume becomes. v/n As the volume of a gas changes due to change of its temperature and pressure, so the molar volume also changes due to change of temperature and pressure. It has been experimentally proved that at standard temperature and pressure, i.e., at STP, the value of the molar volume of any gaseous material is more or less the same and its limiting value is 22.4 L or 22400 mL. This volume is called the molar volume of a gas at STP. So, at STP, 22.4 litres of every gas contain equal number of molecules. From this experimental result, scientist Avogadro postulated his famous eory regarding volume and molecules of any gaseous material. This theory is known as Avogadro’s hypothesis.
Q.5 Explain how Avogadro’s law combines Gay-Lussac’s law and Dalton’s atomic theory.
Ans. It is known that hydrogen chloride (HCI) gas is formed when hydrogen (H) gas and chlorine (CI) gas react with each other. The reaction is given by
H2 + Cl2 = 2HCl
According to Gay-Lussacs’s law of gaseous volume, 1 unit volume of H has to react with 1 unit volume of Cl to produce 2 units volume of HCl.
Now, according to Avogadro’s hypothesis,
1 elementary particle of H+1 elementary particle of Cl = 2 elementary particles of HCl
Meanwhile according to Dalton’s atomic theory, the smallest elementary particle of matter is atom which is indivisible. Therefore for hydrogen or chlorine, the elementary particle is molecule rather than an atom.
Atoms and molecules were first differentiated while explaining Gay-Lussac’s gaseous volume from Avogadro’s hypothesis. Hence, Avogadro’s law combined Dalton’s atomic theory and GayLussac’s law of gaseous volume.
Q.6 Show that wet air is lighter than dry air by using the molar masses of water, nitrogen and oxygen.
Or, Give the reason for air to be lighter in rainy season than in winter.
Ans. We know, density = mass/volume · By any means, if the amount of water vapour increases in air, mass of air decreases and as a result, density of air decreases. Amount of nitrogen and oxygen is high in dry air.
Molar mass of nitrogen is 28 g and molar mass of oxygen is 32g. Again, molar mass of water (H2O) = 1 × 2 + 16 = 18 g
Now, suppose, some amount of dry air is taken in a closed vessel. Then, by keeping temperature and volume unchanged, 4 molecules of N2 and 1 molecule of O2 are taken out of the vessel and 5 molecules of H2O are introduced.
In this case, mass (M₁) of (4 molecules of N2 + 1 molecule of O2)

Hence, M2 < M1. Clearly, total mass of wet air inside the vessel is also reduced in this process. As a result, density of wet air inside the vessel is also reduced. Thus, wet air of rainy season is lighter than dry air of winter.
Q.7 Establish the ideal gas equation formed by combining Boyle’s law, Charles’ law and Avogadro’s hypothesis.
Ans. According to Boyle’s law,

where R is the molar gas constant or universal gas constant. This equation is the ideal gas equation for n mol of gas.
Q.8 Write down the basic assumptions of kinetic theory of an ideal gas.
Ans. The basic assumptions of the kinetic theory of an ideal gas are as follows:
- All the gases are composed of many molecules. Molecules of the same gas are of same nature but molecules of different gases are of different nature.
- Gas molecules behave like point masses. So, volume of the molecules is negligible compared to the volume of the vessel.
- Until the molecules collide amongst themselves and with the walls of the vessel, they move in straight lines with uniform speed. As a result of the collision, the motion of the molecules become disorderly.
- The total linear momentum and the total kinetic energy of the molecules before and after the collision remain unchanged.
- No attractive or repulsive force acts within the gas molecules, i.e., there is no potential energy of the molecules and the entire energy is kinetic energy.
Q.9 Give two arguments in favour of the mobility of gas molecules.
Ans. Pressure and diffusion are the two properties of gases which prove that the gas molecules are mobile. Gas molecules always collide amongst themselves and also with the walls of the vessel. A force is exerted on the wall when the gas molecules collide against it. Pressure of a gas is equal to this force per unit area acting perpendicular to the wall of the vessel.
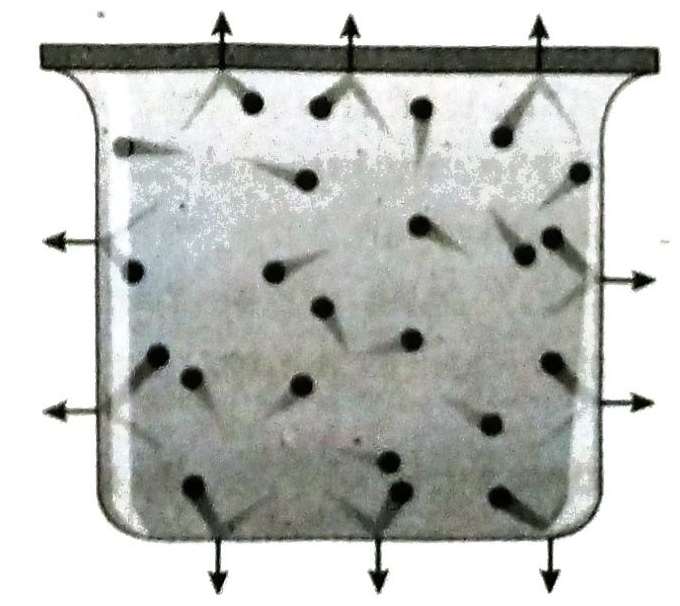
Further, two or more gases mix amongst themselves on their own. This is called diffusion. Therefore, both pressure of a gas and diffusion. arise due to movement of the gas molecules.
Q.10 Discuss the influence of pressure on the volume of a gas.
Ans. If the pressure on an enclosed gas is increased, distance between the molecules decreases. As a result, volume of the gas decreases. Due to decrease in the volume, number of collisions per second on unit area of the wall increases. As a result, pressure of the gas increases and the external pressure and the internal pressure become equal and act in opposite directions. In the same way, if the external pressure is decreased, distances between the molecules increase and as a result, volume increases. Due to increase of the volume, number of collisions per second on unit area of the wall decreases and consequently, the pressure of the gas decreases. Here also, the external pressure and the internal pressure become equal and act in opposite directions.
Q.11 What is diffusion? Which properties of the gas molecules are known due to diffusion?
Or, If an incense stick is ignited inside the room, the fragrance of the stick spreads within the room in a very short time. This phenomenon takes place due to which property of the gas? Write down the reasons.
Ans. Diffusion is the phenomenon by which two or more non-reacting gases (light or heavy) are mixed spontaneously to form a homogeneous mixture, when they come in contact with each other.
If an incense stick is ignited inside a room, the fragrance of the stick spreads within the room in a very short time. As soon as the stick is ignited, there is collision among the gas molecules and also with the molecules of the air. Due to frequent collisions, the direction of motion of the gas molecules gets changed every moment. The intermolecular space is much more than the volume of the gas molecules. As a result, the motion of the molecules of a particular gas enables them to enter into another gas through that intermolecular space and spread within a short time.
So, it is known through the process of diffusion that gas molecules are in motion and their motion is disorderly.
Q.12 Why the volume of a real gas of a definite mass at constant temperature and high pressure does not decrease in accordance with Boyle’s law, even if the pressure on it is increased?
Or, Boyle’s law is applicable for an ideal gas but not for a real gas at high pressure. Why?
Ans. According to the conditions of kinetic theory of gases, total volume of the molecules of a gas is negligible compared to the volume occupied by the gas. But molecules of a real gas, though small, have a finite volume. If pressure is increased, the above mentioned condition remains valid upto a pressure of 1 atmosphere, but at higher pressure the molecules of the gas come very near to each other. As a result, when the pressure is increased on the real gases already kept at high pressure, their volumes do not decrease likewise according to Boyle’s law.
Q.13 How is the presence of intermolecular forces responsible for deviation of a real gas from an ideal gas?
Ans. The pressure of a real gas is less than that of an ideal gas at same temperature and for same mass and volume. This is a deviation of an ideal gas from a real gas.
Explanation: When a gas molecule remains inside the vessel and is slightly away from the wall of the vessel, then it experiences an equal attractive force by the molecules all around it from every direction. As a result, resultant force on that molecule becomes zero. But when a molecule is very near the wall of the vessel, then the molecules inside the vessel and away from the wall exert an inward resultant force on that molecule. As a result, the velocity of the molecule is reduced and thus strikes the wall at a lower speed. Now according to the kinetic theory of an ideal gas, there are no intermolecular forces between the molecules. So, real gas exerts comparatively less amount of pressure on the wall due to the presence of intermolecular forces.

Q.16 Mention two observations which prove the presence of mutual attractive forces between the gas molecules.
Ans. The following two observations prove the presence of intermolecular forces in a real gas:
- Any gas gets condensed into liquid at a definite temperature when its temperature is reduced. Explanation: When temperature is reduced, kinetic energy of the gas molecules is also reduced. As a result, the molecules come nearer to each other only due to mutual attractive force. More the molecules come nearer to each other, more the value of intermolecular force increases. Hence, the gas gets condensed into liquid.
- The pressure of a real gas is slightly less than the pressure of an ideal gas under similar conditions.
Explanation: When a molecule comes very near to the wall of a closed vessel, then that molecule exerts comparatively less force on the wall. This is due to the fact that the molecule which has come closer to the wall of the vessel is attracted by the other molecules away from the wall. So, pressure of the gas is slightly less than the pressure of an ideal gas under similar conditions.
VERY SHORT ANSWER TYPE QUESTIONS
Choose the correct answer
1. Real gases behave like ideal gas at
A. high pressure and low temperature
B. low pressure and high temperature
C. low pressure and low temperature
D. high pressure and high temperature
Ans. B
2. Molar mass of water is
A. 16 g
B. 18 g
C. 20 g
D. 22 g
Ans. B
3. Mass of 5 mol hydrogen gas is
A. 5g
B. 10g
C. 20g
D. 15 g
Ans. B
4. During collision of molecules of an ideal gas
A. only linear momentum remains conserved
B. only kinetic energy remains conserved
C. both linear momentum and kinetic energy remain conserved
D. neither linear momentum nor kinetic energy remains conserved
Ans. C
5. Energy of the molecules of an ideal gas is
A. only potential energy
B. only kinetic energy
C. the sum of potential energy and kinetic energy
D. the difference of kinetic energy and potential energy
Ans. B
6. Which quantity is a constant in the equation pV = nRT?
A. p
B. V
C. T
D. R
Ans. D
7. Value of universal gas constant in CGS system is
A. 8.31 × 106 erg · mol-1 . K-1
B. 8.31 × 107 erg · mol-1 . K-1
C. 8.31 × 108 erg · mol-1 . K-1
D. 8.31 × 109 erg · mol-1 . K-1
Ans. B
8. If x number of molecules are present in volume V of He gas at pressure p and temperature T, then the number of molecules present in a volume 3V of O2 gas at the same pressure and temperature is
A. x
B. 3x
C. x/3
D. 9x
Ans. B
9. The freezing point of water in absolute scale is
A. 0 K
B. 273 K
C. 373 K
D. 173 K
Ans. B
10. According to the kinetic theory of gases, at what temperature the molecule of an ideal gas has zero kinetic energy?
A. 273 K
B. 300 K
C. 0 K
D. 100 K
Ans. C
11. 84g N2 = how many moles?
A. 1
B. 2
C. 3
D. 4
Ans. C
12. What is the molecular mass of CO2 when mass of 11.2 L of CO2 at STP is 22g?
A. 22
B. 44
C. 88
D. 11
Ans. B
13. Number of molecules present in 7g of N2 gas is
A. 12.044 × 1023
B. 1.506 × 1023
C. 3.011 × 1023
D. 6.022 × 1023
Ans. B
14. The amount of work done by expansion of 1 mol ideal gas against fixed pressure when its temperature is increased by 1 K is
A. R
B. 2R
C. 3R
D. 4R
Ans. A
15. The volume of 2.2 g of CO2 at 27°C and a pressure of 570 mm of mercury column is
A. 4.92 L
B. 0.82 L
C. 3.28 L
D. 1.64 L
Ans. D
16. The behaviour of real gases show maximum deviation from the behaviour of ideal gas under
A. low pressure and low temperature
B. low pressure and high temperature
C. high pressure and low temperature
D. high pressure and high temperature
Ans. C
Answer in brief
1. At low temperature or high temperature do the real gases roughly follow the equation pV = KT?
Ans. Real gases roughly follow the equation pV = KT at high temperature.
2. How is the pressure of a definite mass of gas related to the motion of its molecules?
Ans. Keeping the volume of a definite mass of gas constant, if the velocity of the molecules of the gas increases, pressure of the gas inside the vessel also increases.
3. What is molar volume?
Ans. The volume occupied by one gram mole of any gaseous substance (elementary or compound) at a fixed temperature and pressure is called the gram molar volume or molar volume.
4. Does the value of molar volume depend on the nature of the gas?
Ans. No, the value of molar volume does not depend on the nature of the gas.
5. The value of molar volume depends on which factor?
Ans. The value of molar volume depends on the pressure and temperature of the gas.
6. What is the limiting value of molar volume of any real gas at STP?
Ans. The limiting value of molar volume of any gaseous material at STP is 22.4 L or 22400 mL.
7. What is meant by the volume of a gas in Avogadro’s hypothesis?
Ans. Volume of a gas in Avogadro’s hypothesis means the volume of the space occupied by the gas.
8. Who is the first scientist to differentiate between atoms and molecules?
Ans. Avogadro is the first scientist to differentiate between atoms and molecules.
9. How to reduce the density of air of a place at a definite temperature?
Ans. If the amount of water vapour at a place at a definite temperature increases due to som reason, density of air gets reduced.
10. The number of molecules in a balloon filled with hydrogen gas is N. What is the number of molecules in a balloon filled with equal volume of nitrogen at the same temperature and pressure?
Ans. The number of molecules in a balloon containing equal volume of nitrogen gas at the same temperature and pressure is also N.
11. Between dry air and wet air, which one has less density?
Ans. Wet air has less density than dry air.
12. Is there any change in the kinetic energy of the gas molecules in a perfectly elastic collision?
Ans. In a perfectly elastic collision, kinetic energy of the gas molecules remains conserved.
13. The fragrant fumes of a burning incense stick placed at one corner of the room are perceived by smell at another corner of the room. Which property of the gas molecules is demonstrated by this?
Ans. The property of motion of gas molecules is demonstrated by this.
14. The fragrant fumes of a burning incense stick placed at one corner of the room are perceived by smell at another corner of the room. What information about the motion of the gas molecules is available from this phenomenon?
Ans. Due to the mutual collisions of the gas molecules, there is a continuous change in their directions-this information is available from the given phenomenon.
15. What is the number of molecules in 22.4 L of a gas at STP?
Ans. The number of molecules in 22.4 L of a gas at STP is 6.022 × 1023.
16. How can the pressure of a certain quantity of a gas kept in a closed vessel and attached with a piston be increased without changing its temperature?
Ans. The pressure of gas inside the closed vessel increases if the piston is pushed inside the vessel, without changing the temperature.
17. What is the difference between an ideal gas and a real gas on the basis of intermolecular forces?
Ans. Though the value of intermolecular forces in the case of an ideal gas is zero, it is not so in the case of a real gas.
18. Write down the ideal gas equation for n mol of a gas.
Ans. The ideal gas equation for n moles of a gas is pV = nRT.
19. Write down the ideal gas equation for 1 mol of a gas.
Ans. The ideal gas equation for one mole of a gas is pV = RT.
20. Is the equation pV = nRT applicable in the same way to all ideal gases?
Ans. Yes, the equation pV = nRT is applicable in the same way to all ideal gases.
21. What is the unit of universal gas constant R in CGS system and SI?
Ans. The unit of universal gas constant R in CGS system and SI are erg mol-1.K-1 and J. mol-1. K-1, respectively.
22. What is the value of universal gas constant R in cal mol-¹. K-¹?
Ans. The value of universal gas constant in calmol-1. K-¹ is 1.987.
23. What is the value of universal gas constant R in L.atm.mol-1. K-¹?
Ans. The value of universal gas constant in L.atm.mol-1. K-1 is 0.082.
24. What is the relation between the volume of the gas and the total volume of the molecules in case of an ideal gas?
Ans. In case of an ideal gas, total volume of the molecules of the gas is considered to be negligible as compared to the volume occupied by the gas.
25. What is the nature of the collision between two molecules of an ideal gas?
Ans. The collision between two molecules of an ideal gas is an elastic collision because both linear momentum and kinetic energy are conserved in this case.
26. What is the nature of the energy of gas molecules?
Ans. The gas molecules possess kinetic energy.
27. What is condition of diffusion?
Ans. According to the condition of diffusion, when two or more gases which do not react with each other are kept in contact, they may undergo diffusion.
28. Can diffusion take place against gravitation?
Ans. Yes, diffusion can take place against gravitation.
29. A real gas can be converted into liquid by reducing its temperature. What can be inferred about intermolecular force from this phenomenon?
Ans. This phenomenon gives a preliminary idea about the intermolecular force in a real gas.
30. Due to which condition of kinetics, the pressure of an ideal gas is greater than the pressure of a real gas under the same condition?
Ans. The condition that there is no attraction or repulsion amongst the molecules of an ideal gas is responsible for the given occurrence.
31. What is the net attractive force on the molecules of a gas when it remains inside a vessel?
Ans. The net attractive force on the molecules of the gas is zero when it remains inside a vessel.
32. When does a net attractive force act on the molecules of a gas inside a vessel?
Ans. A net attractive force acts on the molecules of a gas inside a vessel when they are very close to the wall of the vessel.
33. Is it possible to convert an ideal gas into a liquid?
Ans. As there is no attractive force amongst the molecules of the ideal gas, hence it is not possible to convert an ideal gas into a liquid.
34. Is it possible to convert a real gas into a liquid?
Ans. As attractive forces are present amongst the molecules of the real gas, it is possible to convert a real gas into a liquid.
Fill in the blanks
1. There is …………. force of attraction between the molecules of an ideal gas.
Ans. no
2. If the pressure of a definite mass of gas is quadrupled at constant temperature, ……….. becomes one fourth.
Ans. volume
3. Mass of 2 mol of CO2 at STP is ………..
Ans. 88 g
4. Volume of 4g of H2 at STP is …………..
Ans. 44.8 L
5. Molar mass of water is ………..
Ans. 18 g.mol-1
6. Value of molar volume does not depend on the …………. of the gas.
Ans. nature
7. If the number of molecules present in 2 g of H2 at STP is N, then the number of molecules present in 64g of O2 at STP is ……….
Ans. 2N
8. If Avogadro number is N, then number of molecules present in 8.5g of NH3 gas is …………
Ans. N/2
9. If the temperature of an enclosed gas increases, then kinetic energy of the molecules also …………
Ans. increase
10. Compared to the time required by a gas molecule to traverse its free path, the time of collision is ………..
Ans. negligible
11. During collision of two molecules, both linear momentum and ………….. are conserved.
Ans. kinetic energy
12. Force of attraction ………….. between molecules of a real gas.
Ans. exists
13. Value of pV/T for one mole of an ideal gas is …………..
Ans. R
14. Moist air is ……………. than dry air.
Ans. lighter
16. Unit of molar mass in CGS system is ………….
Ans. g · mol-1
State whether true or false
1. One mole of any gas at STP occupies 22.4 L volume and 6.022 × 1023 molecules.
Ans. True
2. Value of molar volume depends upon the nature of the gas.
Ans. False
3. Real gases behave like ideal gases at low pressure and high temperature.
Ans. True
4. Mean free path of a gas molecule is inversely proportional to the number of molecules per unit volume.
Ans. True
5. The collision between two molecules of an ideal gas is an inelastic collision.
Ans. False
6. The value of universal gas constant in L · atm · mol-1 · K-1 is 0.082.
Ans. True
7. Dimensional formula for universal gas constant is ML2T2NΘ-1.
Ans. False
8. In case of an ideal gas, volume of the gas molecules is neglected.
Ans. True
9. At constant pressure, the density of a gas is inversely proportional to its absolute temperature.
Ans. True
10. The value of R in the equation pV = RT, depends on the values of p , V and T.
Ans. False
11. Total kinetic energy of the molecules of a gas at 0 K is zero.
Ans. True
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here