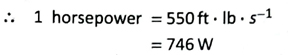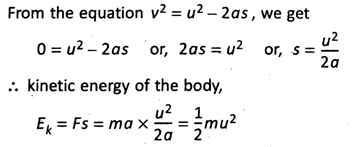WBBSE 9th Class Science Solutions Physical Science & Environment Chapter – 5 Work, Power and Energy
West Bengal Board 9th Class Science Solutions Physical Science & Environment Chapter – 5 Work, Power and Energy
WBBSE 9th Class Physical Science & Environment Solutions
Synopsis
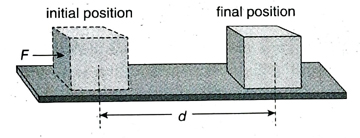
- When on object is displaced from its initial position under the action of a force, then I work is said to be done. Work is a scalar quantity.
- If d is the displacement of the object and F is the force applied, then work done, W = Fd.
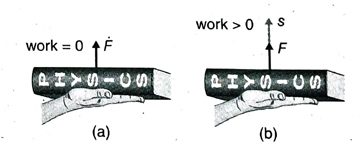
- During application of force on a body, if the body gets displaced in the direction of the applied force, then work is said to be done by the force. This is also called positive work.
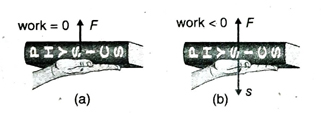
- During application of force on a body, if the body gets displaced in the direction opposite to that of the applied force, then work is said to be done against the force. This is also called negative work.
- When the displacement of an object is at an angle of 90° with the direction of force, then no work is done by the applied force. This type of force is called no-work force.
- Dimensional formula of work is ML²T-².
- In CGS system and SI, the absolute units of work are erg and joule or J respectively.
TOPIC – A
Work
SHORT AND LONG ANSWER TYPE QUESTIONS
1. Define work. How is the quantity of work measured?
Ans. When an object is displaced from its initial position under the action of a force, then work is said to be done.
If applying a force F on a body displaces it by a distance d in the direction of the force, then work done, W=Fd.
2. What do you mean by work done by a force or positive work? Explain with examples.
Ans. During application of force on a body, if the body gets displaced in the direction of the applied force, then work is said to be done by the force. Since force and displacement are in the same direction, the value of this work is positive. Hence, it is called positive work.
For example, when a book is raised upward from the ground, work is said to be done by the force and is positive as the displacement of the book takes place in the same direction as that of the applied force.
3. What do you me mean by work done against a force or negative work? Explain with examples.
Ans. During application of force on a body, if the body gets displaced in the direction opposite to that of the applied force, then work is said to be done against the force. Since applied force and displacement are in the opposite directions, the value of this work is negative. Hence, it is called negative work.
For example, when a book is lowered slowly with constant velocity, an upward force is applied on the book at every moment. In this case, work is said to be done against the force and it is negative work as the displacement of the book takes place in the opposite direction as that of the applied force.
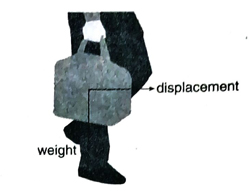
4. What is no-work force? Give two examples of no-work force.
Ans. When the displacement of an object takes place in a direction perpendicular to the direction of the force, then no work is done by the applied force. This type of force is called no-work force.
Examples:
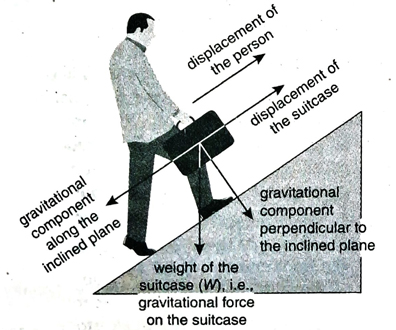
(1) A man walks along a horizontal path with a suitcase in his hands. Force of gravity acts downward on the suitcase, but in a direction perpendicular to the displacement of the suitcase. Here, force of gravity is a no-work force [Fig.].
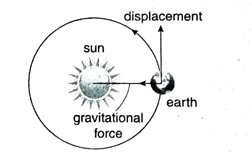
(2) Let us assume that due to the gravitational force of the sun, the earth is moving in circular orbits around the sun. At any position of the earth, the gravitational force acts along the radius towards the centre of the orbit and the direction of displacement is along the tangent at that point of the circular path. This force of the sun on the earth is a no-work force since the direction of displacement of the earth at every point of its orbit is perpendicular to the force [Fig.).
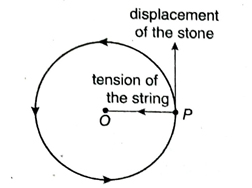
5. A stone attached to a thread, is rotated around a finger in a horizontal plane. Which force is working in which direction due to this rotation? What is the direction of the displacement of the stone at any moment? Give reasons in favour of your answer. Explain how much work is done by you due to this rotation.
Ans. A strong pull is felt by the finger due to rotation of the stone. The faster this stone is rotated, the more this pull is experienced. The stone rotates due to the pull toward the centre along the radius of the circle (along the thread in this case). This force is called centripetal force.
It can be said from experience that if the thread breaks during rotation by any means, then no force is applied on the stone through the thread. The stone is dislodged tangentially from the circular path. This means that during revolution, the direction of displacement of the stone is always tangential to the circle.
The pull of the thread is along the radius of the circle and the displacement of the stone is tangential to the circle. This means that applied force and displacement are perpendicular to each other. Hence, this force on the stone is a no-work force.
6. A man is walking up an inclined plane with a box in his hand. Is the gravitational fatione force doing any work on the box?
Ans. In Fig., it is shown how gravity attracts the box in a straight downward direction.
As a result, a component of gravity, W₂ works downward along the inclined plane. But the displacement of the box takes place in upward direction along the inclined plane. So, gravity is doing positive work in this case.
7. In a tug-of-war game, both the sides pull the rope with equal strength in opposite directions. What is the amount of work done by each side?
Ans. In a tug of war game, both the sides pull the rope with equal strength but there is no displacement of the rope towards either side. As there is no displacement of the point of application of force, no work is done by the applied force and hence, the work done by each side is zero.
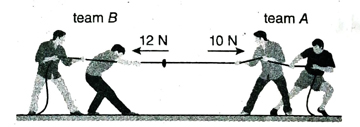
8. In a tug-of-war game between teams A and B, team A which applies a force of 10N is defeated by team B which applied a force of 12 N. In this case, which team has done positive work and which team has done negative work?
Ans. In a tug-of-war game, team B has won. This means that team B has applied comparatively more force than team A. So, displacement of team A has taken place towards team B. In this case, point of application of force i.e., displacement of team A has taken place towards direction of force applied by team B. Hence, team B has done positive work.
On the other hand, team A has also applied a force of 10 N on team B. In spite of that, displacement has taken place towards team B. Actually, team B has slided backwards in the game. Hence, it may be said that displacement of team B was brought about by team A against the direction of force. So, team A has done negative work.
9. A motor car is running on a horizontal road with uniform velocity. Is the engine of the car doing work in this condition?
Ans. Friction of the ground works against the motion of the car when it moves on a horizontal plane. To maintain uniform velocity of the car, its engine applies a force equal to the frictional force in the direction of movement and for displacement of the car against friction, the engine of the car works. If the velocity of car=v; frictional force = F, then work done by the engine per second = Fv.
10. A man walks to the top of a hill along a steep path. Another man having the same mass as the first one, goes to the top via a complex route. Which individual does greater amount of work?
Ans. Work done by an object or an individual is the product of the force applied on it and the displacement of the object or individual.
As the masses of the two men are the same in this case, so their weights are also same. This means that each man has applied the same force against his weight to climb the hill.
Again, displacement is defined as the linear distance between the initial and final positions of the moving object or individual. In this case, displacements for both the men are the same as they have climbed the top of the hill from the ground level. As a result, both have done the same work.
[Note: Frictional force has not been taken into account in the given case. In reality, different amounts of frictional forces act on them while climbing the hill. Hence, the amount of work done by the two men is different in that case.]
11. A man is swimming against the current in such a way that he is stationary with respect to the shore. Is he doing any work?
Ans. As there is no displacement with respect to the shore, no work is done with respect to the shore. But there is displacement with respect to the river water, so work done by the man is not zero with respect to water.
VERY SHORT ANSWER TYPE QUESTIONS
Choose the correct answer
1. Which of the following vehicles does more work to traverse a fixed distance in the same path carrying the same weight?
A. bullock cart
B. bicycle
C. horse cart
D. same work is done by all the vehicles
Ans. D
2. Unit of work in Sl is
A. watt
B. erg
C. joule
D. dyne
Ans. C
3. In a tug of war,
A. the defeated team does positive work
B the defeated team does negative work
C. the victorious team does negative work
D. no work is done by either of the teams
Ans. B
4. A body makes a complete round in a circular path and during its journey, average applied force on it was F, r being the radius of the circular path. What is the total amount of work done by the body?
A. zero
B. 2лгF
C. 2rF
D. лrF
Ans. A
5. Gravitational force is a no-work force. This is because
A. displacement of the body does not occur in the direction of gravitational force
B. displacement of the body occurs in a direction perpendicular to the direction of gravitational force
C. displacement of the body occurs in the direction opposite to that of gravitational force
D. there is no displacement of the body
Ans. B
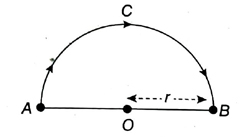
6. A body starts its journey from point A, traverses a path ACB and reaches point B. Average applied force, F acts on the body during the entire course of its journey. If the path ACB is semicircular with a radius r, the amount of work done by the body is
A. Zero
C. πrF
C. 2лrF
D. 2rF
Ans. D
7. A body held in hand is brought downward. Here, work is done against the force because
A. the direction of applied force is downward
B. the direction of gravitational force on the body is downward
C. the direction of displacement of body is downward
D. the direction of force applied on the body is upward but displacement of the body is downward
Ans. D
8. Work done by winding the spring of a manual-winding watch is stored in the watch as
A. sound energy
B. kinetic energy
C. potential energy
D. light energy
Ans. C
9. Suppose you start racing from a fixed position in a field and come back to the same place. What is the total work done?
A. zero
B. positive quantity
C. negative quantity
D. none of these
Ans. A
10. The angle between the applied force and displacement in the case of no work force is
A. 0°
B. 45°
C. 90°
D. 180°
Ans. C
11. The work done on an object does not depend upon the
A. force applied
B. initial velocity
C. displacement
D. angle between force and displacement
Ans. B
Answer in brief
1. Product of two vector quantities is a scalar quantity. Give an example.
Ans. Force and displacement are vector quantities but their product, work is a scalar quantity.
2. Give an example of no-work force.
Ans. Centripetal force is a no-work force.
3. What is the dimensional formula of work?
Ans. Dimensional formula of work is ML²T-².
4. What is the absolute unit of work in SI?
Ans. The absolute unit of work in Sl is joule (J).
5. What is the absolute unit of work in CGS system?
Ans. The absolute unit of work in CGS system is erg.
6. 1J = how many erg ?
Ans. 1J= 107 erg
7. What is the angle between force and displacement in case of no-work force?
Ans. In case of no-work force, angle between force and displacement is 90°.
8. How much work is done by a weight-lifter when he stands with a weight above his head?
Ans. As the weight-lifter stands still with the weight above his head without any displacement, no work is done by him.
9. The earth moves around the sun due to the force exerted by the sun on the earth. Is any work being done by the sun due to this motion of the earth?
Ans. No, force of attraction or gravitational force of the sun on earth is a centripetal force which is a no-work force.
10. Does work depend on the speed with which a body is raised upward?
Ans. No, work done depends on displacement of the body and not on the speed with which the body is raised upward.
11. Apart from no-work force, is it possible for the value of work done to be zero in any other case?
Ans. Yes, if the displacement of a body is zero even after the application of force, amount of work done is zero.
12. What is the value of work related to potential energy in a place where gravity is zero?
Ans. Value of work related to potential energy in a place of zero gravity is zero.
13. In a tug of war game, which side does work when the rope remains motionless?
Ans. As there is no displacement of the rope, none of the sides is doing any work.
14. A book is raised upward with uniform velocity. In this case, is work being done against the force or by the force?
Ans. As the displacement of the book is in the direction of the applied upward force, work is being done in favour of the force.
15. A book is lowered downward with uniform velocity. In this case, is work being done against the force or by the force?
Ans. As the displacement of the book is downward but the book is held using an upward force, work is done against the force.
16. A book held in hand, is displaced horizontally with uniform velocity. What is the relationship between force and work in this case?
Ans. In this case, the applied force is a no-work force.
17. Can we recover the work done under a force?
Ans. Work done can be recovered if it is done under a force where mechanical energy is conserved.
18. A stone is thrown upward. Is work being done by or against the force of gravity?
Ans. In this case, work is done against the force of gravity since displacement of the stone is upward but gravitational force acts downward.
19. When is work done by a force positive?
Ans. work done by a force is positive when the displacement of the body is in the direction of the force.
20. When is work done by a force negative?
Ans. Work done by a force is negative, when the displacement of the body is in the direction opposite to the direction of the force.
21. How much work is done by a weight-lifter when he stands with a weight above his head?
Ans. If the weighter-lifter stands still with the weight above his head without any displacement, no work is done by him.
22. Does work depend on the speed with which a body is displaced?
Ans. No, work done depends on displacement of the body, not on the speed with which the body is displaced.
23. What is the work done by the force of gravity on a satellite moving round the earth?
Ans. The force of gravity acts at right angle to the displacement of the satellite, so work done is zero.
Fill in the blanks
1. Work is a ………… quantity.
Ans. scalar
2. The applied force does not do any work if the angle between force and displacement is …………
Ans. 90°
3. Centripetal force is a ……….. force.
Ans. no-work
4. Any car traversing the same path carrying the same weight does the same amount of ………….
Ans. work
5. Negative work denotes that work is done ……….. the force.
Ans. against
6. A boy fails to lift a water-filled bucket in spite of his attempts. Amount of work done by the boy is …………
Ans. zero
7. Work done by the string of a simple pendulum during oscillation is ……….
Ans. zero
8. ………… work is done when a mass is taken up with constant velocity by holding it in hand.
Ans. Positive
State whether true or false
1. It is said that work has been done when there is displacement of an object due to the application of an external force on a body.
Ans. True
2. Negative work is done when the point of application of force moves in a direction opposite to that of the applied force.
Ans. True
3. It is said that work has been done when there is displacement of an object due to the application of an external force on a body.
Ans. True
4. Positive work is done when the point of application of force moves in a direction of the applied force. 4
Ans. True
5. When an airplane takes off the work done by its weight is positive.
Ans. False
6. Work is a vector quantity.
Ans. False
7. In a tug-of-war the stronger team does positive work.
Ans. True
TOPIC – B
Power
SHORT AND LONG ANSWER TYPE QUESTIONS
1. Define power. What is the relationship between power and work done?
Ans. Power is defined as the rate of doing work with respect to time.
If amount of work W is done in time t, then power, P = W/t.
2. What is the dimensional formula of power? What are the dimensions of power?
Ans. Dimensional formula of pwer
Dimensions of power are 1 in length, 2 in mass and-3 in time.
3. What is the relationship between power and velocity?
Ans. We know, power = work (W) / time (t)
Suppose a small displacements of a body takes place in the direction of a constant force F while being acted on the body for a time t.
∴ work done, W = Fs
So, power, P = W/t = Fs/t = Fv, where v is the instantaneous velocity and time interval t is very small.
4. Suppose a man walks a distance of 3 m in a horizontal path in 5 s with a bucket of water in hand. Then he climbs up 3 m in a staircase in 5 s with the same bucket. Explain in which case, the man has more power.
Ans. While walking in a horizontal plane with a bucket in hand, the force of graving acts in a direction opposite to the weight of the bucket. But the displacement of the bucket is horizontal, i.e., in a direction perpendicular to the force applied on the bucket. Hence, this is a no-work force. As the amount of work is zero, value of power is also zero. But while going up the staircase with the bucket, work is done against gravity. As a result, value of power is not zero. Hence, power is more in the second case.
5. What do you mean by kilowatt and horsepower?
Ans. Kilowatt: 1 kW (kilowatt) is defined as the power of doing 1000J of work in 1 s. So, 1 kW = 1000 W.
Horsepower: 1 horsepower is defined as the power of doing 550 ft lb of work by any machine or by a system in 1s.
6. The power of an engine is 5 horsepower. What do you mean by the above statement?
Ans. As 1 hp = 746 W, 5 hp = 5 × 746 = 3730 W. That is, the power of the engine is 3730 W. This means that the engine can do a work of 3730 J per second.
7. Sand is falling from the lower portion of a sand filled moving truck. How does the kinetic energy of this truck change if the power spent by the engine remains unchanged?
Ans. Power of the engine of the moving truck
In this case, due to the fall of sand from the truck, its mass (m) decreases gradually. But according to the question, in order to keep the power spent by the engine constant, the velocity (v) of the truck has to be increased in the same proportion. Thus, the value of the quantity mg x v remains constant.
Since, v increases in spite of mv remaining constant, hence the kinetic energy of the truck increases in this case.
VERY SHORT ANSWER TYPE QUESTIONS
Choose the correct answer
1. The product of applied force on a body with its speed gives a measure of its
A. power
B. energy
C. work
D. momentum
Ans. A
2. Horsepower is the unit of which of the following physical quantities?
A. work
B. power
C. kinetic energy
D. potential energy
Ans. B
3. Amount of work done by a machine of 1000W power in 1 minute is
A. 60000 J
B. 1000 J
C. 600 J
D. 100 J
Ans. A
4. A body is lifted from the ground slowly to a certain height in the first case. Again in the second case, the same body is lifted more rapidly to the same height from the ground. Which of the following statements is true?
A. Though the amount of work done is same in both the cases, amount of power is higher in the first case
B. Though the amount of work done is same in both the cases, amount of power is higher in the second case
C. In both the cases, work and power are different
D. In both the cases, work and power are same
Ans. B
5. 100W is written on an electric bulb. W is the unit for which quantity?
A. electrical energy
B. electrical power
C. electrical work
D. mechanical energy
Ans. B
6. Power of the engine of a motorbike is generally expressed in which unit?
A. horsepower
B. watt
C. joule/second
D. erg/second
Ans. A
7. Which of the following physical quantities has joule/hour as its unit?
A. work
B. kinetic energy
C. force
D. power
Ans. D
8. Rate of doing work by a body with respect to time is called
A. force
B. power
C. energy
D. linear momentum
Ans. B
9. Compared to one kilowatt (kW), one horsepower (hp) is
A. more
B. less
C. same
D. cannot be said
Ans. B
10. A train moves against a frictional force of 5000 N at a velocity of 25 m/s. What is the power of the engine of the train?
A. 1250 W
B. 125000 J/s
C. 1.25 × 106 W
D. 12.5 W
Ans. B
11. A boy does a work of 400 erg in 5s and a girl takes 10s to do the same work. Which of the following statements is correct?
A. The boy has more power
B. The girl has more power
C. Both have the same power
D. None of the above
Ans. A
12. Which of the following physical quantity have the unit J/h?
A. work
B. kinetic energy
C. force
D. power
Ans. D
Answer in brief
1. What is the unit of power in Sl?
Ans. Watt is the unit of power in Sl.
2. What is the relationship between work and power?
Ans. Relationship between work and power is expressed by power = work/time
3. What is the relationship between power and velocity?
Ans. Relationship between power and velocity is expressed by
power = applied force × velocity of the body
[In this case, velocity of the body means instantaneous velocity.]
4. Horsepower is the unit of which quantity?
Ans. Horsepower is the practical unit of power in FPS system.
5. 1 horsepower = how many W?
Ans. 1 horsepower = 746 W.
6. 1 kW = how many horsepower?
Ans. 1 kW 1.34 horsepower
7. What do you mean by 1 kilowatt of power?
Ans. One kW (kilowatt) is defined as the power required to do a work of 1000J in one second, i.e., 1 kW = 1000 W.
8. The power of a pump is 1.2 kW. What do you mean by the above statement?
Ans. The power of a pump is 1.2 kW means that the pump can do a work of 1.2 kJ or 1200 J in one second.
Fill in the blanks
1. Division of the unit of work by the unit of power gives the unit of …………….
Ans. time
2. Multiplication of the unit of force by the unit of ………… gives the unit of power.
Ans. velocity
3. Power × ………….. = work.
Ans. time
4. Power is a ………… physical quantity.
Ans. scalar
5. Power of a motor is 373 W. In hp unit the power of the motor is ………….
Ans. 0.5
6. Power of an agency depends upon how fast ………… is done by it.
Ans. work
State whether true or false
1. Power is a scalar quantity.
Ans. True
2. Power is the capacity of a body to do work.
Ans. False
3. 1 horsepower = 746 kW.
Ans. False
4. Rate of work done is power.
Ans. True
5. Horsepower is a practical unit of power.
Ans. True
6. The power of a pump is 1 kW – means that the pump can perform 1000 J work in 1 s.
Ans. True
TOPIC – C
Energy
SHORT AND LONG ANSWER TYPE QUESTIONS
1. What is energy? What is its dimensional formula? What are its units in CGS system and Sl?
Ans. Energy is the capacity of a body to do work.
Energy is measured by the amount of work a body can do. So, units and dimensional formulas of energy and work are the same.
Dimensional formula of energy is ML²T-².
Units of energy in CGS system and SI are erg and joule, respectively.
2. Name different forms of energy.
Ans. Energy is present in nature in different forms. These are- 1. mechanical energy, 2. heat energy, 3. chemical energy, 4. sound energy, 5. electric energy, 6. magnetic energy, 7. light energy, 8 atomic energy.
3. What is mechanical energy? How many types of mechanical energy are there? Name them.
Ans. Mechanical energy is the energy that is possessed by an object due to its motion or position or change of configuration or due to all these three.
Mechanical energy is of two types: 1. kinetic energy and 2. potential energy.
4. What is kinetic energy? Establish the formula for kinetic energy of a body of mass m moving with velocity u.
Ans. Kinetic energy is the energy acquired by a body by virtue of its motion.
Suppose, a body of mass m is moving in a straight line with velocity u. A constant force F is applied against the motion of the body to bring it to rest after traversing a distance s.
As the body has traversed a distance s against a force F, it has the capacity to do Fs amount of work. Hence, its kinetic energy = Fs.
If a is the deceleration of the body for applying force F against its motion, then a = F/m.
It stops after travelling a distance s, so its final velocity, v = 0.
5. Can the kinetic energy of a body be negative? Explain.
Ans. The formula for measuring the kinetic energy of a body is 1/2mv², where m is its mass and v is its velocity.
The value of m can never be negative. On the other hand, v² is a squared quantity and hence its value can never be negative. So, kinetic energy of a body cannot be negative.
6. A body with kinetic energy 10J is thrown upward. If air resistance is ignored, what is the potential energy of the body at the highest point?
Ans. At the highest point, the kinetic energy of the body becomes zero. Hence, according to the law of conservation of energy, potential energy becomes 10J.
7. Explain elastic potential energy and gravitational potential energy with examples.
Ans. A stone is thrown from a rubber catapult with a high velocity. Here, when the rubber band is stretched to increase its length, it develops a capacity to work which enables it to throw the stone with high velocity. This energy of the stretched string is potential energy in nature and is called elastic potential energy.
Again, work is done if a body is raised to some height against gravity. Then, it also develops some capacity to work. For example, if a hammer is placed on a nail standing erect on the ground, it does not pierce the ground but if the hammer is raised to some ight and then hit straight on the top of the nail, the nail enters a bit into the ground. Here, displacement of the nail is due to application of force by the hammer. In this case, when the hammer is raised upward, it develops the capacity of doing work. We may say that some amount of gravitational potential energy is stored in the hammer in this way.
8. Give an example of the potential energy of a body due to change of its position.
Ans. Hydroelectricity is produced by confining water in a raised place with a barrier. In this case, potential energy is stored in water due to change of its position.
9. Give an example of the potential energy of a body due to change of its shape.
Ans. The energy used by an archer to pull the string back in his bow is stored in the elastic material of the bow. This is an example of potential energy due to change of shape.
10. A body has energy but no momentumis this situation possible?
Ans. Yes, it is possible. A body when thrown upward, it stops for a moment at the highest point. At that moment, it has no momentum but has gravitational potential energy.
11. A ball is kept on the top of a staircase. Is it possible to know without disturbing the ball, if there is any mechanical energy in it? How would one know if there is any potential energy stored in it?
Ans. The ball is at rest on the top of the staircase. If it is not disturbed, it will forever remain in this state. This is due to the law of inertia. This means that the ball is an inert object and does not move itself. Thus, if it is not disturbed, it cannot do any work. As energy is defined as a measure of the ability of a body to do work, unless the ball is shaken (disturbed), external manifestation of energy in it is not possible. So, it is not known whether there is any mechanical energy in the ball or not.
As the ball is pushed from the top of the staircase, it starts rolling down the staircase. As a result, it may be said that the ball possesses kinetic energy. As energy cannot be created, so it may be reasoned that the potential energy stored in the ball changes into this kinetic energy. Hence, in this way we come to know that gravitational potential energy is stored in this ball while it is on the top of the staircase.
12. Write and explain the law of conservation of mechanical energy.
Ans. According to the law of conservation of mechanical energy, in the absence of any dissipative force (e.g. friction, air resistance etc.), the total mechanical energy of a body or an agency always remains constant.
A stone is thrown up in a perpendicular direction. The more it goes up, more is the decrease of its velocity and finally, it comes to rest for a moment. Then it starts falling downwards and as it comes down, its velocity increases. The stone was thrown upwards with a definite velocity or definite kinetic energy. Now as it goes up, its velocity decreases and kinetic energy also decreases. But its potential energy increases equivalently.
If air resistance is ignored, it can be proved that the decrease in kinetic energy of the stone is equal to the increase in its potential energy. That is, at any moment in its state of motion, the sum of kinetic energy and potential energy of the stone or total mechanical energy remains constant. There is only a transformation from kinetic energy to potential energy or potential energy to kinetic energy. For example, at the highest point, the stone stops for a moment and at that time, there is no kinetic energy of the stone. Entire kinetic energy has been converted to potential energy. Next, when the stone drops downwards, then the potential energy decreases and the kinetic energy increases. As the stone continues to drop down, its velocity continues to increase.
VERY SHORT ANSWER TYPE QUESTIONS
Choose the correct answer
1. When the speed of a body is doubled, its kinetic energy becomes
A. doubled
B. quadrupled
C. halved
D. quartered
Ans. B
2. When both the mass and the speed of a body is doubled, its kinetic energy becomes
A. four times
B. eight times
C. ten times
D. half
3. Energy is
A. the rate of doing work
B. the capacity of doing work
C. the power of doing work
D. all of the above
Ans. B
4. Amount of energy accumulated by a piece of stone falling freely just before touching the ground is
A. total kinetic energy
B. total potential energy
C. equal amounts of kinetic energy and potential energy
D. heat energy and sound energy
Ans. A
5. The mechanical energy of a body thrown upward is
A. maximum at the highest point
B. minimum at the highest point
C. highest at the moment of just touching the ground
D. same at all points
Ans. D
6. Total energy of an oscillating simple pendulum for which the theory of conservation of mechanical energy holds good is
A. maximum at the central position
B. maximum at the terminal position
C. minimum at the central position
D. always constant
Ans. D
7. In question no. 6, kinetic energy of the pendulum is
A. maximum at the central position
B. maximum at the terminal position
C. minimum at the central position
D. always constant
Ans. A
8. In question No. 6, potential energy of the pendulum is
A. maximum at the central position
B. maximum at the terminal position
C. minimum at the central position
D. always constant
Ans. B
9. Two objects have the same kinetic energy but their masses are in the ratio of 4:9. Ratio of linear momentum of the objects is
A. 4:9
B. 9:4
C. 2:3
D. 3:2
Ans. C
10. Ratio of masses of two objects is 1:2 and ratio of their kinetic energies is 2:1. What is the ratio of their linear momentum?
A. 1:1
B. 2:1
C. 1:2
D. 1:4
Ans. A
11. Linear momentum of two objects is same but the ratio of their masses is 2:3. Ratio of kinetic energies of these two objects is
A. 3:2
B. 2:3
C. 4:9
D. 9:4
Ans. A
12. With increasing height of a body from the surface of the earth, the value of its gravitational potential energy
A. increases
B. decreases
C. remains same
D. none of the above
Ans. A
13. One empty lorry and a similar lorry loaded with goods are moving with the same speed. Which one of them has greater kinetic energy?
A. loaded
B. empty
C. both have the same energy
D. none of the above
Ans. A
14. Which of the following statements is not false?
A. A moving body has no kinetic energy
B. Potential energy is stored in a compressed spring
C. Unit of power is W/m²
D. Dimensional formula of work is ML-²T²
Ans. B
15. Mechanical energy is the sum of which of the following energies?
A. kinetic energy and potential energy
B. light energy and chemical energy
C. sound energy and light energy
D. heat energy and light energy
Ans. A
16. If the kinetic energy of a moving object increase by 20%, its linear momentum increases by
A. 10%
B. 11%
C. 20%
D. 21%
Ans. A
17. If a body moves with retardation its kinetic energy
A. decreases
B. increases
C. remain unchanged
D. increases first and then decreases
Ans. A
Answer in brief
1. What is the relationship between kinetic energy and the momentum of a body of mass m?
Ans. If E is the kinetic energy of the mass m, its linear momentum, P = √2mE.
2. If a body is raised some distance from the earth’s surface and then released, which energy is transformed to which energy?
Ans. In this case, gravitational potential energy stored in the body is transformed into its kinetic energy.
3. What is the nature of energy conversion in the case of an arrow being shot from a bow?
Ans. An archer stores potential energy in the bow by bending its string which gets converted to kinetic energy when the arrow is shot.
4. What is the condition of applicability of the law of conservation of mechanical energy?
Ans. Condition for applicability of the law of conservation of mechanical energy is that no dissipative force should be present.
5. If air resistance is taken into consideration, is mechanical energy conserved in case of a body falling under gravity?
Ans. No, if air resistance is taken into consideration, mechanical energy is not conserved in case of a body falling under gravity.
6. A body has momentum but no energy-is this situation possible?
Ans. No, it is not possible because if a body has momentum, it must have kinetic energy.
7. What is the dimensional formula of kinetic energy?
Ans. Dimensional formula of energy is ML²T-².
8. Mechanical energy is the sum of which energies?
Ans. Mechanical energy is the sum of kinetic energy and potential energy.
9. What is the relationship between work and energy?
Ans. Energy is the capacity of a body to do work.
10. What is the relationship between the units of work and energy?
Ans. Energy is measured in the same unit as that of work.
11. What is potential energy?
Ans. Energy acquired by a body by virtue of its position or configuration is called its potential energy.
12. Name the type of energy possessed by a raised hammer.
Ans. Potential energy.
Fill in the blanks
1. When the velocity of a body is doubled, then its kinetic energy is …………
Ans. quadrupled
2. When the kinetic energy of a body is increased nine times, linear momentum becomes ………..
Ans. three times
3. If two bodies have different masses but same kinetic energy, then the ………. body has more momentum.
Ans. heavier
4. If two bodies with different masses but same momentum, then the ………. body will have less kinetic energy.
Ans. heavier
5. A body of mass m is released from a height h. If resistance due to air is neglected, its kinetic energy at a distance of h/2 from the ground is ………..
Ans. mgh/2
6. According to the law of conservation of energy, ………….. can neither be created nor destroyed.
Ans. energy
7. Total mechanical energy of a body is ………… when it falls under the influence of gravity.
Ans. conserved
8. Kinetic energy ………….. be negative.
Ans. cannot
9. Gravitational potential energy ………….. be negative.
Ans. can
10. If a bullet is fired from a gun, kinetic energy of the bullet is …………. than the kinetic energy of the gun.
Ans. greater
11. If the kinetic energies of two bodies of mass Im and 4m are in the ratio 2:1, then ratio of the momentum of the bodies is ……….
Ans. 1: √2
12. Gravitational potential energy is present due to existence of …………
Ans. gravitation
13. ………… is the energy acquired by a body by virtue of its motion.
Ans. Kinetic energy
14. Energy is expressed in the unit of ………….
Ans. work
State whether true or false
1. In Sl, the absolute unit of energy is joule (J).
Ans. True
2. Energy acquired by a body by virtue of its position or configuration is called its kinetic energy.
Ans. False
3. If a body changes its position against gravity, it gains certain amount of energy which is called gravitational potential energy.
Ans. True
4. Kinetic energy of a body can be negative.
Ans. False
5. Mechanical energy of a freely falling body is conserved.
Ans. True
6. Linear momentum of a body of mass m and kinetic energy E is 2mE.
Ans. False