JKBOSE 10th Class Maths Solutions chapter – 10 Circles
JKBOSE 10th Class Maths Solutions chapter – 10 Circles
J&K 10th Class Maths Solutions chapter – 10 Circles
Jammu & Kashmir State Board JKBOSE 10th Class Maths Solutions
INTRODUCTION
We have studied in Class IX that a circle is a collection of all points in a plane which are at a constant distance (radius) from a fixed point (centre). We have also studied various terms releated to a circle like chord, segment, sector, arc etc. Let us now examine the different situations that can arise when a circle and a line are given in a plane.
Consider a circle and a line PQ. There can be three possibilities given in Fig. below:
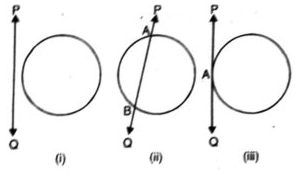
In Fig. (i), the line PQ and the circle have no common point. In this case, PQ is called a nonintersecting line with respect to the circle. In Fig. (ii), there are two common points A and B that the line PQ and the circle have. In this case, we call the line PQ a secant of the circle. In Fig. (iii), there is only one point A which is common to the line PQ and the circle. In this case, line is called a tangent to the circle.
We might have seen a pulley fitted over a well which is used in taking out water from the well. Look at Fig. Here the rope on both sides of the pulley, if considered as a ray, is like a tangent to the circle representing the pulley.
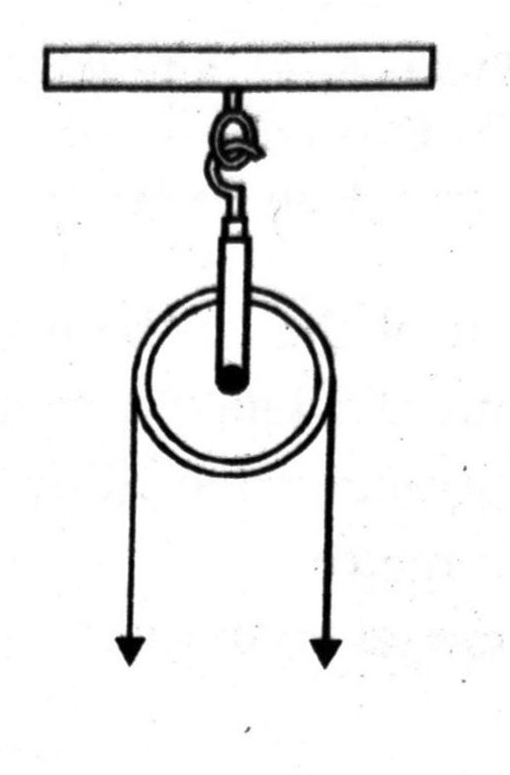
In this chapter, we will study about the existence of the tangents to a circle and also study some of their properties.
TEXT BOOK EXERCISE 10.1
Q. 1. How many tangents can a circle have?
Solution. Since at any point on a circle, there can be one and only one tangent. But circle is a collection of infinite points, so we can draw infinite number of tangents to a circle.
2. Fill in the blanks :
(i) A tangent to a circle intersects it in………. point(s).
(ii) A line intersecting a circle in two points is called a…………
(iii) A circle can have …….. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ………….
Solution.
(i) A tangent to a circle intersects it in one point.
(ii) A line intersecting a circle in two points is called a secant.
(iii) A circle can have two parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called point of contact.
Q. 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D)√119 cm.
Solution. According to given information we draw the figure such that,
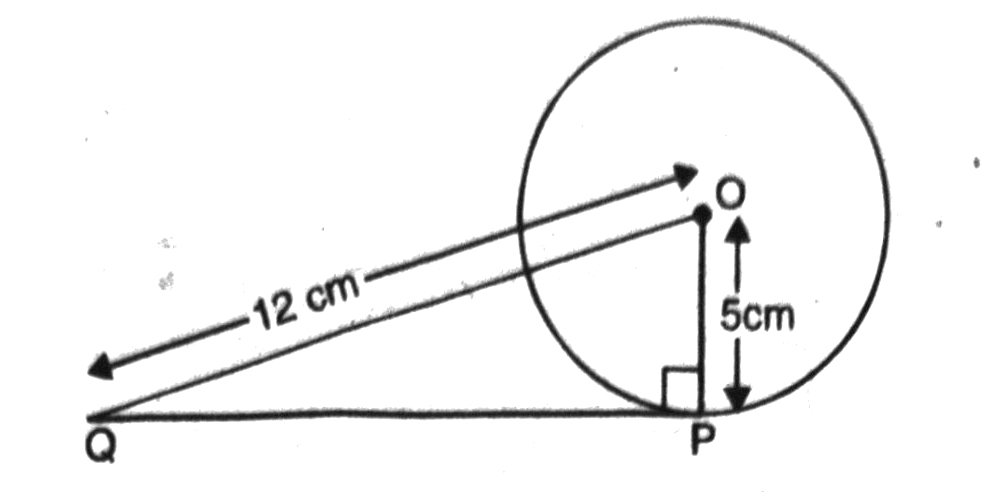
OP = 5 cm and OQ = 12 cm
∵ PQ is a tangent and OP is the radius
∴ ∠OPQ = 90°
Now, in right angled Δ OPQ,
By Pythagoras Theorem,
OQ² = OP² + QP²
Or (12)² = (5)² + QP²
Or Qp² = (12)² – (5)²
Or QP² = 144 – 25 = 119
Or QP = √119 cm.
Hence, option (D) is correct. Ans.
Q.4. Draw a circle and two lines parallel to a given line such that one is a tangent and other a secant to the circle.
Solution. According to the given information we draw a circle having O as centre and I is the given line.
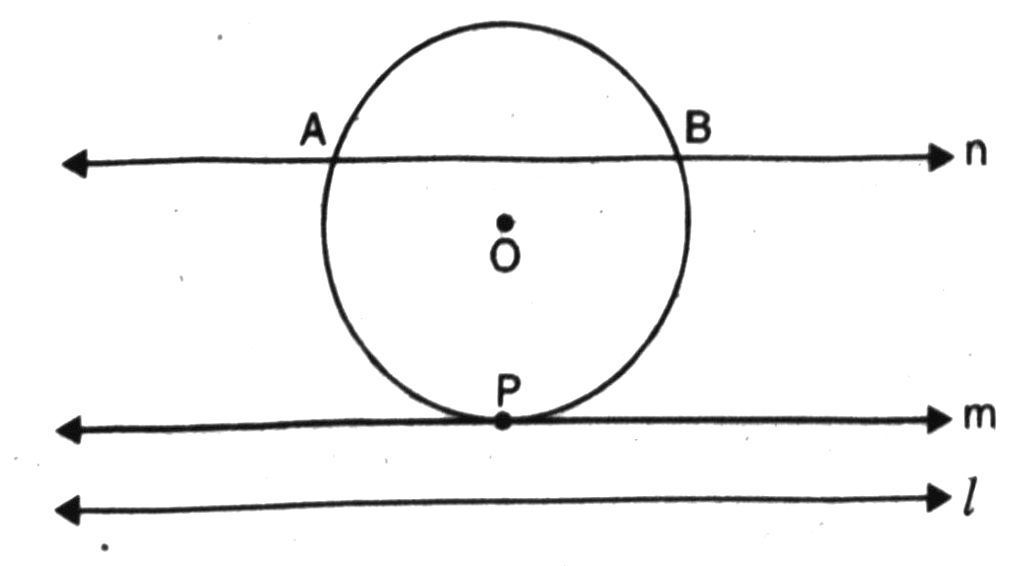
Now, m and n be two lines parallel to a given line l such that m is tangent as well as parallel to l and n is secant to the circle as well as parallel to l.
TEXT BOOK EXERCISE 10.2
In Q. 1 to 3, choose the correct option and give justification.
Q. 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Solution. A circle with centre O from a point, the length of the tangent to a circle is 24 cm and distance of Q from the centre is 25 cm.
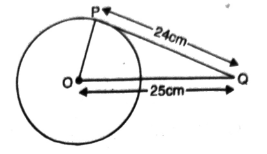
∴ ∠QPO = 90°
Now, in right angled ΔQPQ,
OQ² = PQ² + OP²
(25)² = (24)² + OP²
or 625 = 576 + OP²
or OP² = 625 – 576
or OP² = 49 = (7)²
or OP = 7 cm
∴ Option (A) is correct. Ans.
Q. 2. In Fig., if TP and TQ and two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°.
If TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110°, then find ∠PTQ.
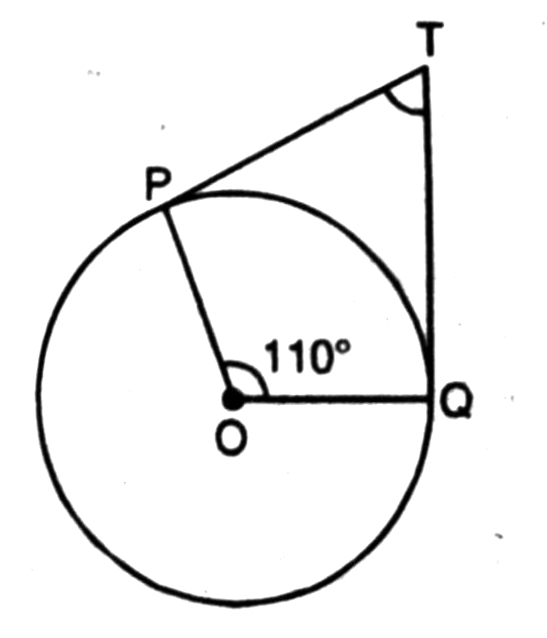
Solution. In figure, OP is radius and PT is tangent to circle.
∴ ∠OPT = 90°
Similarly, ∠OQT 90° and ∠POQ = 110° (Given)
Now, POQT is a Quadrilateral.
∴ ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
110° + 90° + ∠QTP + 90° = 360°
Or ∠QTP + 290° = 360°
Or ∠QTP = 360°-290°
Or ∠QTP = 70°
∴ Option (B) is correct. Ans.
Q. 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°.
Solution. In given firgure, OA is radius and AP is a tangent to the circle.
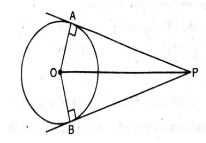
∴ ∠OAP = 90°
Similarly, ∠OBP = 90°
Now, in right angled ΔPAO and ΔPBO
∠PAO = ∠PBO = 90°
OP = OP (Common side)
OA = OB (radii of same Circle)
∴ ∠PAO ≅ ΔPBO [RHS congruence]
∴ ∠AOP = ∠BOP [CPCT]
Or ∠AOP = ∠BOP = 1/2 ∠AOB ….(1)
Also, In Quad. OAPB,
∠OBP + ∠BPA + ∠PAO + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
∠AOB = 360° – 260°
∠AOB = 100° …(2)
Form (1) and (2), we get
∠AOP = ∠BOP = 1/2 × 100° = 50°
∴ option (A) is correct. Ans.
Q. 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution. Given. A circle with center O and AB as its diameter l and m are tangents at points A and B
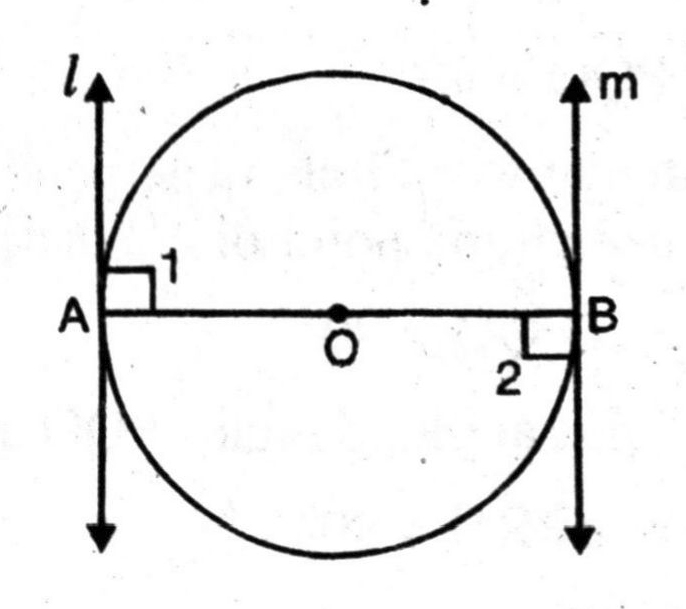
To Prove. l || m
Proof. OA is the radius and I is the tangent. to the circle.
∴ ∠1 = 90°
Similarly, ∠2 = 90°
Or ∠1 = ∠2 = 90°
But these are alternate angles between two lines, when one transversal cuts them.
∴ l || m
Hence, tangents drawn at the ends of a diameter of a circle are parallel.
Q. 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution. Given. A circle with centre O. AB its tangent meet circle at P.
i.e., P is the point of contact
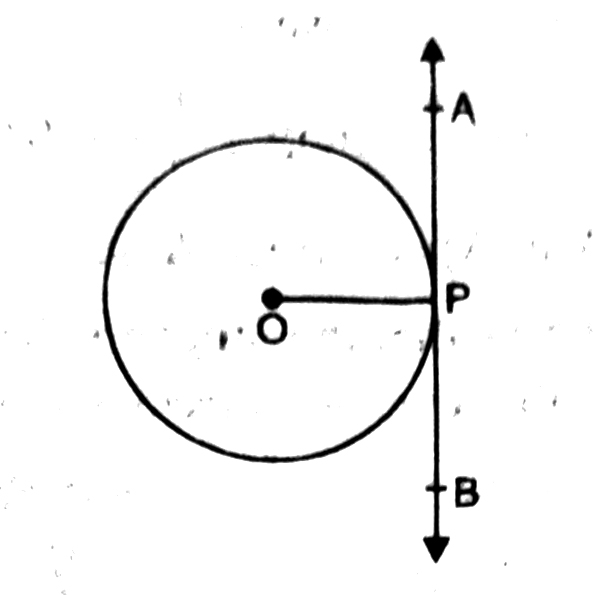
To Prove. Perpendicular at the point of contact to the tangent to a circle passes through the centre.
Construction. Join OP.
Proof. The perpendicular to a tangent line AB through the point of contact passes through the centre of the circle because only one perpendicular, OP can be drawn to the line AB through the point P.
Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre.
Q. 6. The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm find the radius of the circle.
Solution. A circle with centre ‘O’ A is any point outside the circle at a distance of 5 cm from the centre.
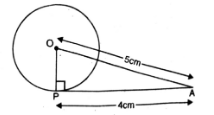
Length of tangent = PA = 4 cm
Since, OP is the radius and PA is the tangent to the circle.
∴ ∠OPA = 90°
Now, in right angled ΔOPA,
Using Pythagoras Theorem,
OA² = OP² + PA²
(5)² = OP² + (4)²
Or OP² = 25 – 16
Or OP² = 9 = (3)²
Or OP = 3 cm.
Hence, radius of the circle is 3 cm. Ans.
Q. 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution. Two concentric circles having same centre O, and radii 5 cm and 3 cm respectively. Let PQ be the chord of larger circle but tangent to the smaller circle.
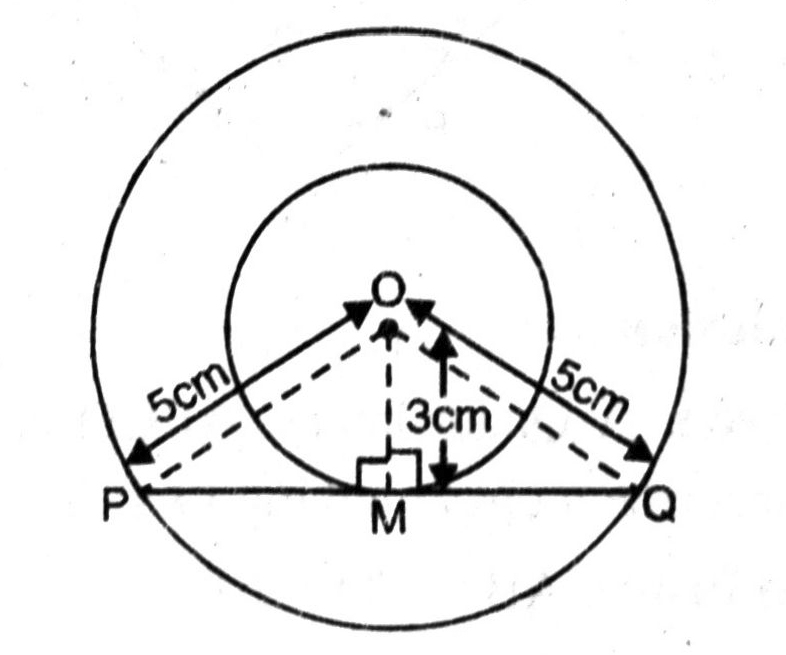
Since, OM be the radius of smaller circle and PMQ be the tangent.
∴ ∠OMP = ∠OMQ = 90°
Consider, right angled triangles OMP and OMQ,
∠OMP = ∠OMQ = 90°
OP = OQ [radii of same circle]
OM = OM [common side]
∴ ΔOMP ≅ OMQ [RHS congruence]
∴ PM MQ [CPCT]
Or PQ = 2 PM = 2 MQ
Now, in right angled Δ OMQ,
Using Pythagoras Theorem,
OQ² = OM² + MQ²
(5)² = (3)² + (MQ)²
Or MQ² = 25 – 9
Or MQ² = 16 (4)²
Or MQ = 4 cm
Length of chord PQ = 2 MQ = 2 (4) cm = 8 cm
Hence, length of required chord is 8 cm. Ans.
Q. 8. A quadrilateral ABCD is drawn to the circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
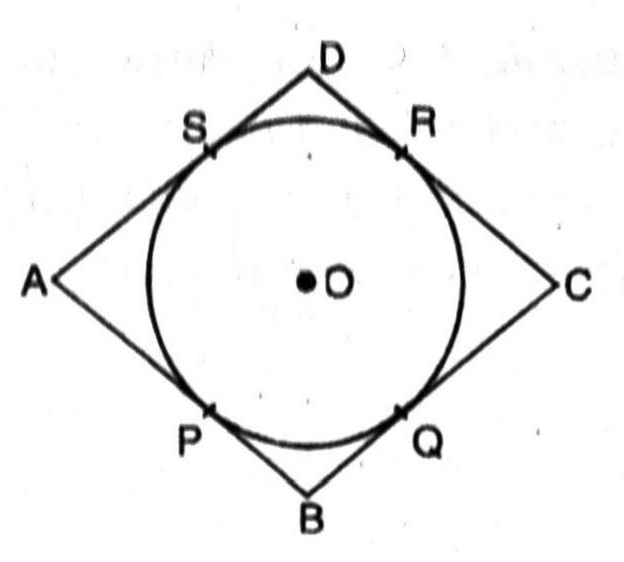
Solution :
Given. A Quadrilateral ABCD is drawn to circumscribe a circle having O as its centre.
To Prove. AB+CD = AD + BC
Proof. Since the lengths of tangents drawn from an external point to a circle are equal.
Now, B is any point outside the circle and BP; BQ are tangents to the circle.
∴ BP = BQ …(1)
Similarly, AP = AS …(2)
and CR = CQ …(3)
Also, DR = DS …(4)
Adding (1), (2), (3) and (4), we get
(BP + AP) + (CR + DR) = (BQ + CQ) + (AS + DS)
AB + CD = BC + AD
is the required result.
Q. 9. In figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°
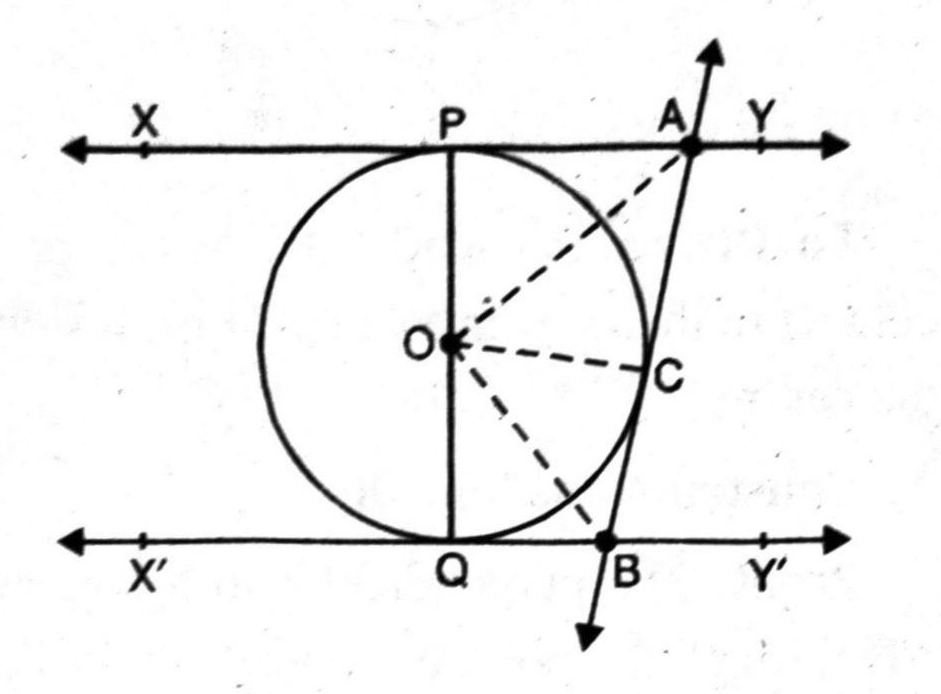
Solution. Given. A circle with centre O having two parallel tangents XY and X’Y’ and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B.
To Prove. ∠AOB = 90°
Contruction. Join OC, OA and OB.
Proof. Since the lengths of tangents drawn from an external point to a circle are equal.
Now, A is any point outside the circle from two tangents PA and PC are drawn to the circle.
∴ PA = PC
Also, in A POA and Δ AOC,
PA = PC (Proved)
OA = OA (common side)
OP=OC (radii of same circle)
∴ ΔPOA ≅ ΔAOC [SSS congruence]
and ∠PAO = ∠CAO [CPCT]
Or ∠PAC = 2 ∠PAO = 2 ∠CAO …(1)
Similarly, ∠QBC = 2 ∠OBC = 2 ∠OBQ …(2)
Now, ∠PAC + ∠QBC = 90° + 90° = 180°
[Sum of the interior angles on the same side of transversal is 180%],
Or 2∠CAO + 2∠OBC = 180°
[Using (1) & (2)]
Or ∠CAO + ∠OBC = 180°/2 = 90° …(3)
Now, in ΔOAB,
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180°
[Using (3)]
Or ∠AOB = 180° – 90° = 90°
Hence, ∠AOB = 90°
Q. 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution. Given. A circle with centre O. P is any point outside the circle from PQ and PS are the tangents to the given circle.
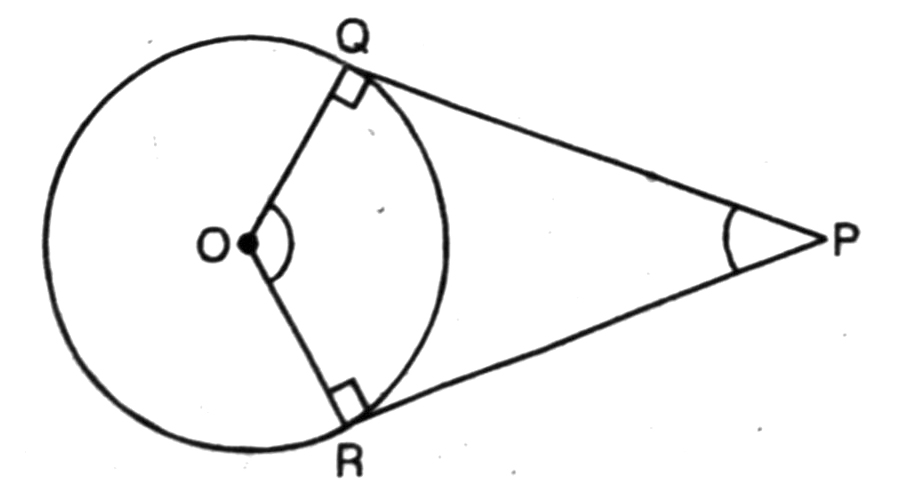
To Prove. ∠ROQ + ∠QPR = 180°
Proof. OQ is the radius and PQ is tangent from point P to the given circle.
∴ ∠OQP = 90° …(1)
[∵ The tangent at any point of a circle is perpendicular to the radius through the point of contact]
Similarly, ∠ORP = 90° …(2)
Now, in quadrilateral ROQP,
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
Or ∠ROQ + 90° + 90° + ∠QPR = 360°
[Using (1) & (2)]
Or. ∠ROQ + ∠QPR + 180 = 360°
Or ∠ROQ + ∠QPR = 360° – 180°
Or ∠ROQ + ∠QPR = 180°
Hence, the angle between the two tangents drawn from and external. point to a circle is supplementary to angle subtended by the line segment joining the points of contact at the centre.
Q. 11. Prove that the parallelogram circumscribing a circle is a rhombus.
Solution. Given. A parallelogram ABCD circumscribed a circle with centre O.
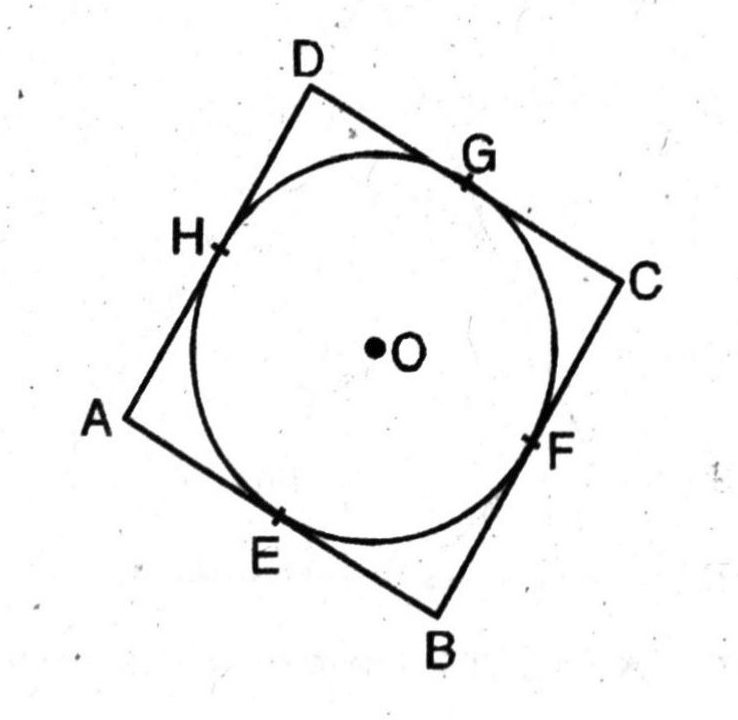
To Prove. ABCD is a rhombus.
Proof. Since the lengths of tangents drawn from an external point to a circle are equal. Now, B is any point outside the circle and BE; BF are tangents to the circle.
∴ BE = BF …(1)
Similarly, AE = AH …(2)
and CG = CF …(3)
Also DG = DH …(4)
Adding (1), (2), (3) and (4), we get
(BE + AE) + (CG + DG)
= (BF + CF) + (AH + DH)
Or AB + CD = BC + AD …(5)
Now, ABCD is a parallelogram,
∴ AB = CD and BC = AC …(6)
From (5) and (6), we get
AB + AB = BC + BC
Or 2AB = 2BC or AB = BC
Or AB = BC = CD = AD
∴ ABCD is a rhombus.
Hence, parallelogram circumscribing a circle is a rhombus.
Q. 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig). Find the sides AB and AC.
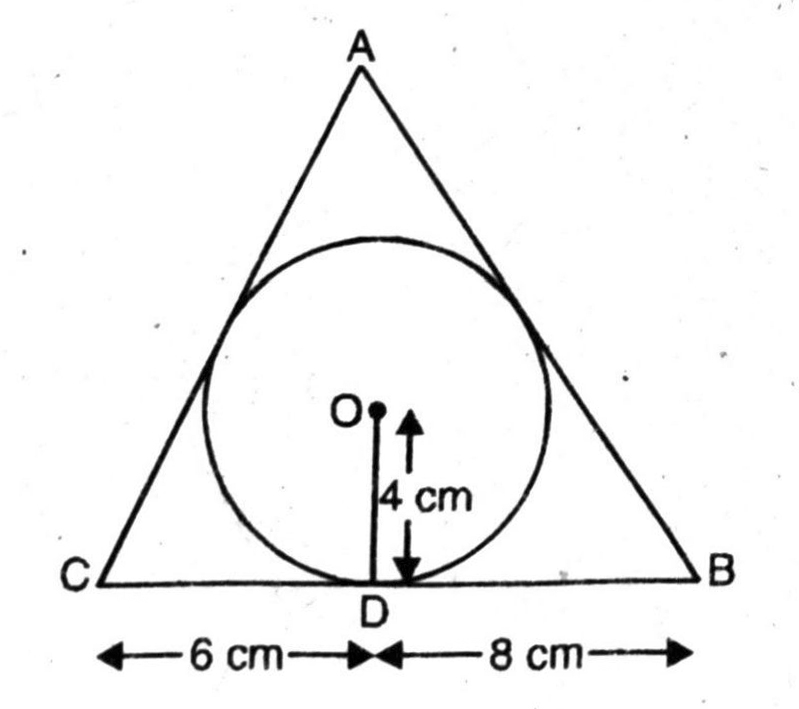
Solution. A triangle ABC is drawn to circumscribe a circle of radius 4 cm and the sides BC, CA, AB of AABC touch the circle at D, E, F respectively. Since the lengths of tangents drawn from on external point to a circle are equal.
∴ AE = AF = x cm (say)
CE = CD = 6 cm
and BF = BD = 8 cm
Since the tangent at any point of a circle is perpendicular to the radius through the point of contact.
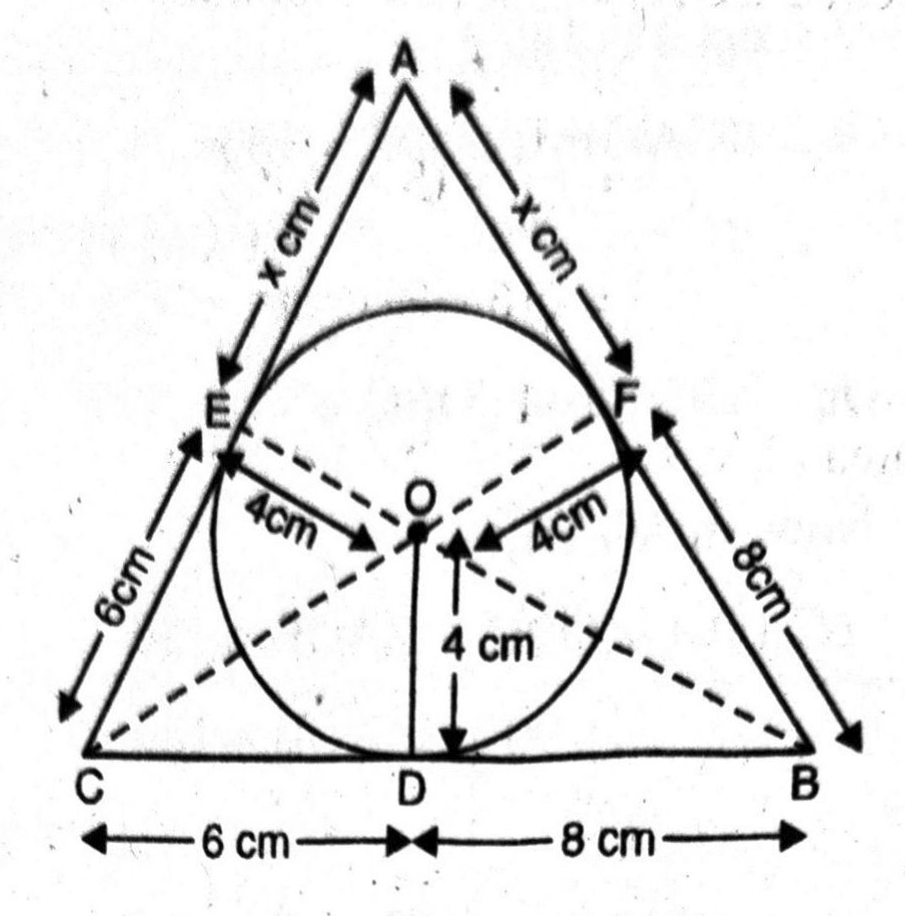
∴ OD ⊥ AB; OE ⊥ AC and OF ⊥ AB.
Also, OE = OD = OF = 4 cm.
Consider, Δ ABC
a = AC = (x + 6) cm;
b = CB = (6 + 8) cm = 14 cm
c = BA = (8 + x) cm


∴ AC = (x + 6) cm
= (7 + 6) cm = 13 cm
and AB = (x + 8) cm
= (7 + 8) cm = 15 cm
Hence, AB = 15 cm AC = 13 cm Ans.
Q. 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Given. A quadrilateral PQRS circumscribing a circle having centre O. Sides PQ, QR, RS and SP touches the circles at L, M, N, T respectively.
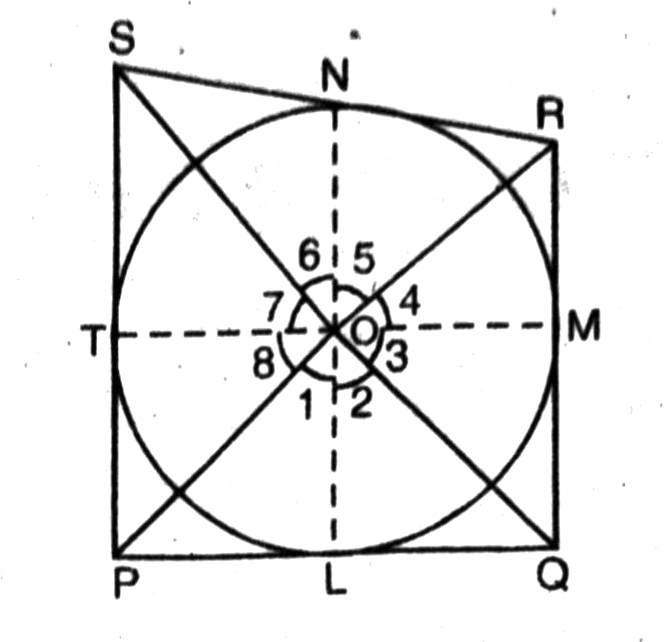
To Prove.
∠POQ + ∠SOR = 180°
and ∠SOP + ∠ROQ = 180°
Construction.
Join OP, OL, OQ, OM, OR, ON, OS, OT
Proof. Since the two tangents drawn from an external point subtend equal angles at the centre.
∴ ∠2 = ∠3; ∠4 = ∠5 ; ∠6 = ∠7; ∠8 = ∠1 …(1)
But, sum of all angles around a point is 360°
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
Or ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
Or 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
Or (∠1 + ∠2) + (∠5 + ∠ 6) = 360°/2 = 180°
Or ∠POQ + ∠SOR = 180°
Similarly, ∠SOP + ∠ROQ = 180°
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here