j&k 10th Maths 

JKBOSE 10th Class Maths Solutions chapter – 11 Construction

Ajit kumar 65 Views 0 Comments

JKBOSE 10th Class Maths Solutions chapter – 11 Construction

J&K 10th Class Maths Solutions chapter – 11 Construction

Jammu & Kashmir State Board JKBOSE 10th Class Maths Solutions

INTRODUCTION

In class IX, we have done certain constructions using a straight edge (ruler) and a compass, e.g. bisecting an angle, drawing the perpendicular-bisector of a line segment, some constructions of triangles etc. and also gave their justification. In this chapter, we shall study some more constructions by using the knowledge of earlier constructions would also be expected to give the mathematical reasoning behind, why such constructions work.

TEXT BOOK EXERCISE 11.1

In each of the questions, give the justification of the construction also.

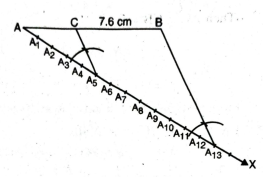
Q. 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5: 8. Measure the two parts.
Solution. Given : A line segment of length of 7.6 cm.
Steps of construction :
  1. Take a line segment AB = 7.6 cm.
  2. Draw any ray AX, making an acute angle ∠BAX.
  3. Locate 5+ 8 = 13 (given ratio 5: 8) points A1, A2, A3, A4, A5…….. A10, A11, A12, A13 on ray AX such that A1 A2 = A2A3 = A3 A4 =….. = A11A12 = A12 A13.
  4. Join BA13.
  5. Through point A5, draw a line A5C || A13B (by making an angle equal to ∠AA13B) at A5 intersecting AB at ‘C’. Then AC : CB = 5:8
Justification :
Let us see how this method gives us the required division.
In ΔAA13B,
Since A5C || A13B
∴ By Basic Proportionality Theorem,
This shows that ‘C’ divides AB in the ratio 5:8.
On measuring the two parts,
AC = 2.9 cm and CB = 4.7 cm
Alternative Method
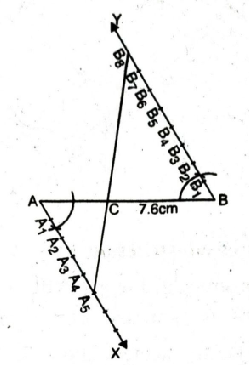
Steps of construction :
  1. Take a line segment AB = 7.6 cm.
  2. Draw any acute angle ∠BAX
  3. Draw angle ∠ABY such that ∠ABY = ∠BAX.
  4. Locate the points A1, A2, A3, A4, A5 on ray AX such that A1 A2 = A2A3 = A3 A4 = A4 A5.
  5. Locate the points, B1, B2, B3, B4, B5, B6, B7, B8 on ray BY such that B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8
  6. Join A3Bg let it intersects AB at point ‘C’.
Then AC CB = 5:8
Justification :
In ΔACA5 and Δ BCB8,
∠ACA5 = ∠BCB8 [vertically opp. ∠s]
∠BAA5 = ∠ABB8 [construction]
∴ ΔACA5 ~ ΔBCB8 [AA-similarity cond.] ..
∴ Their corresponding sides must be in the same ratio.
Hence AC : CB = 5 : 8.
Q. 2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of corresponding sides of the first triangle.
Solution.
Steps of construction :
1. Construct a. triangle ABC with given measurements. AB = 5 cm, AC = 4 cm and BC = 6 cm.
2. Make any acute angle ∠CBX below the side BC.
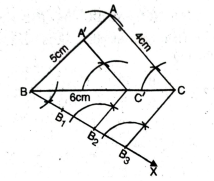
3. Locate three points (greater of 2 and 3 in 2/3) B1, B2, B3, on BX such that BB1 = B1B2 = B2B3.
4. Join B2C.
5. Through B2 (smaller of 2 and 3 in 2/3) draw a line parallel to B3C, which intersect BC in C’.
6. Through C’, draw a line parallel to CA meeting BA is A’.
Thus ΔA’BC’ is the required triangle whose sides are 2/3 of corresponding sides of ΔABC.
Justification of construction :
First we will show that first triangle and constructed triangle are similar.
i.e. ΔA ‘BC’ ∼ ΔABC
Consider ΔA ‘BC’ and ΔABC.
∠B = ∠B                        [Common]
∠A’C’B = ∠ACB           [By construction]
ΔA’C’B ∼ ΔACB           [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
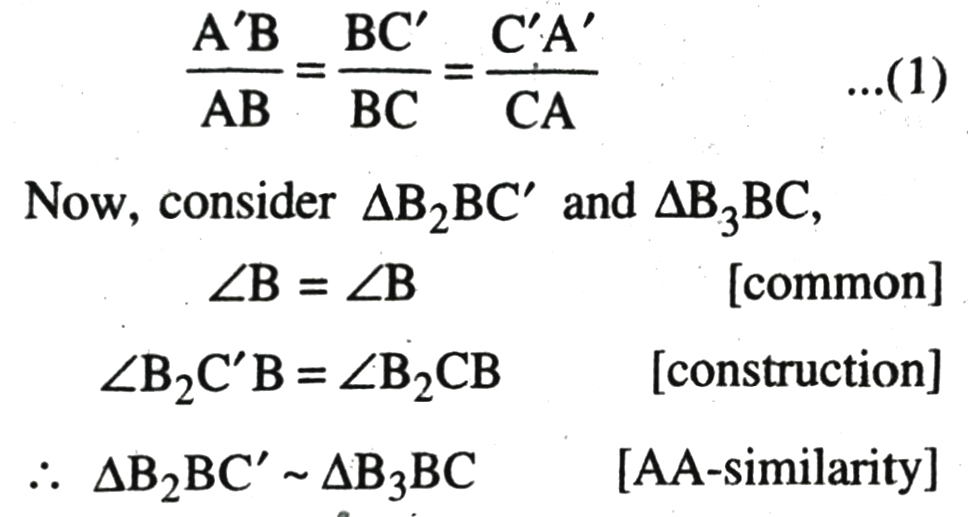
∴ Their corresponding sides must be in the same ratio.
Hence, the construction is Justified.
Q. 3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle. 
Solution.
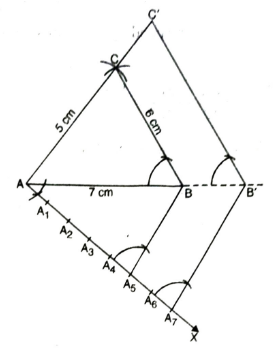
Steps of construction :
1. Construct a triangle ABC in which AB = 7 cm, BC = 6 cm and AC = 5 cm.
2. Make any acute angle ∠BAX below the base AB.
3. Locate seven points A1, A2, A3, A4, A5, A6, A7, on the ray AX such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
4. Join BA5.
5. Through A7, draw a line parallel A5B. Let it meets AB at B’ on being produced such that AB’ = 7/5 AB.
6. Through B’, draw a line parallel to BC which meets AC at C’ on being produced.
ΔAB’C’ is the required triangle.
Justification of the construction.
In ΔABC and Δ AB’C’,
∠A = ∠A    [common]
     ∠ABC = ∠AB’C’ [corresponding ∠s]
∴ ∠ABC ∼ ∠ AB’C’   [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
Again, in Δ AA5B and AA7B’
∠A = ∠A                [common]
∠AA5B = ∠AA7B’           [corresponding ∠s]
∴ ΔΑΑ5Β ~ ΔΑΑ7Β’        [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
Hence, the sides of ΔAB’C’ are 7/5 of ΔABC.
Q. 4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 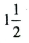times the corresponding sides of the isosceles triangle.
Solution. Given. Base of isosceles triangle is 8 cm and Altitude = 4 cm
To construct: A triangle whose sides are 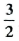 times the sides of isosceles triangle.
Steps of construction : 
1. Take base AB = 8 cm.
2. Draw perpendicular bisector of AB. Let it intersect AB at ‘M’.
3. With M as centre and radius=4 cm, draw an arc which intersects the perpendicular bisector at ‘C’
4. Join CA and CB.
5. ΔABC is an isosceles with CA = CB.
6. Make any acute angle ZBAX below the side BC.
7. Locate three (greater of ‘2’ & ‘3’ in 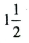or )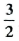
A1, A2, A3 on ‘AX’ such that AA1 = A1 A2 = A2A3.
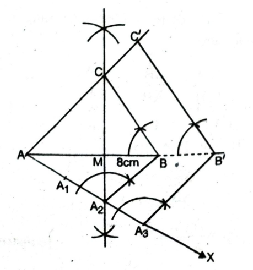
8. Join A₂ (2nd point smaller of ‘2’ and ‘3’ in 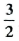)and B.
9. Through A3, draw a line parallel to A2B meet AB is B’ on being produced.
10. Through B’, draw a line parallel to BC which meets AC in C’ on being produced. ΔA B’C’ is the required triangle whose sides are 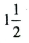times the corresponding sides of ΔABC.
Justification of construction :
First we will prove ΔAB’C’ are ΔABC and similar.
Consider Δ AB’C’ and Δ ABC
∠A = ∠A              [Common]
∠AB’C’ = ∠ABC            [By construction]
ΔAB’C’ ~ ΔABC            [By AA-similarity]
∴ Their corresponding sides must be in the same ratio
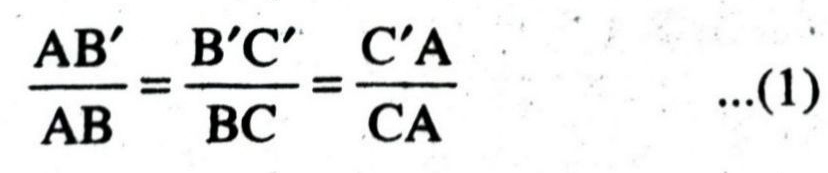
Now consider Δ A3AB’ and Δ A2AB
∠A = ∠A                  [Common]
∠B’A3A = ∠BA2A            [By construction]
∴ ΔΑ3ΑΒ’ ∼ ΔΑ2ΑΒ        [AA-similarity]
∴ Their corresponding sides must be in the same ratio
Hence, given result is justified.
Q.5. Draw a triangle ABC with side BC=6 cm, AB=5 cm and ∠ABC=60°. Then construct a triangle whose sides are ¾ of the corresponding sides of the triangle ABC.
Solution.
Steps of construction :
1. Take a line segment BC = 6 cm
2. Construct an angle of measure 60° at point B. i.e., ∠BAX = 60°.
3. With B as centre and radius 5 cm draw an arc intersecting BX at ‘A’
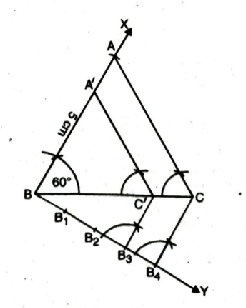
4. Join A and C.
5. At B, make any acute angle ∠CBY below the side BC.
6. Locate four points (greater of 3 and 4 in ¾ ) B1, B2, B3, B4 on BY such that BB1 = B1B2 = B2B3 = B3B4.
7. Join B4 and C.
8. Draw a line through B3 (smaller of 3 and 4 in ¾) parallel to B4C making corresponding angles. Let the line through B3 intersects BC in C’.
9. Through C’, draw a line parallel to CA which intersects BA at A’.
The ΔA’BC’ is the required triangle whose sides are ¾ of sides of ΔABC.
Justification of the construction
Consider ΔA’BC’ and ΔABC,
∠B = ∠B            [common]
∠A’C’B = ∠ACB          [corresponding ∠s]
∴ ΔA’BC’ ∼ ΔABC      [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
Now consider ΔB3B C and ΔB4BC.
∠B = ∠B             [common]
∠C’ B3B = ∠CB4B       [corresponding ∠s]
ΔB3B C’~ AB4BC        [AA-similarity con.]
∴ Their corresponding sides must be in the same ratio.
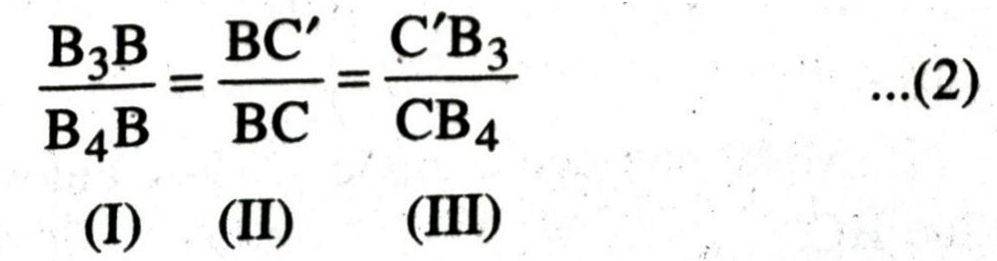
From (I) and (II),
ΔA’BC’ is the required triangle whose sides are ¾ sides of ΔABC.
Q. 6. Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then construct a triangle whose sides are 4/3 times the corresponding sides of ΔABC.
Solution.
Steps of construction :
1. Construct the triangle ABC with the given measurements.
BC=7 cm; ∠B = 45°, ∠A = 105°
By angle sum property of triangle
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C 180 = 150° = 30°
2. Make any acute angle ZCBX at point B, below the sides BC.
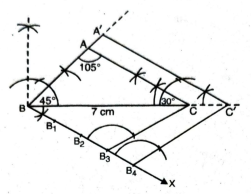
3. Locate four points (greater of 3 and 4 in 4/3) B1, B2, B3, B4 on ‘BX’ such that BB1 = B1B2 = B2B3 = B3B4.
4. Join B3C (smaller of 3 and 4 in 4/3).
5. Through B4, draw a line parallel to B3C meeting BC in C’ on being produced.
6. Through C’, draw another line parallel to CA meeting BA in A’ on being produced.
7. Δ A’BC’ is the required triangle whose sides are 4/3 times the triangle ABC.
Justification of construction
Consider the Δ A’BC’ and Δ ABC,
∠B = ∠B              [common]
∠A’C’B = ∠ACB            [construction]
∴ ΔA’BC’ ∼ ΔABC        [AA-similarity]
∴ Their corresponding sides must be in the same ratio
Again, consider AB4B C’ and AB3BC,
∠B = ∠B            [common]
∠C’B4B = ∠CB3B       [By construction]
∴ Δ B4BC’ ∼ ΔB3BC   [AA-similarity]
∴ Their corresponding sides must be in the same ratio
Hence the construction is justified.
Q. 7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution.
Steps of construction.
1. Draw a right triangle using given conditions. Consider the triangle as ΔABC in which BC = 4 cm; AB = 3 cm and ∠B = 90°.
2. Make any acute angle ∠CBX below the line BC.
3. Locate five points (greater of 5 and 3 in 5/) B1, B2, B3, B4, B5, on BX such that BB1 = B1B2 = B2B3 = B3B4 = B4B5
4. Join B3 (smaller of ‘5’ and ‘3’ in 5/3) and ‘C’.
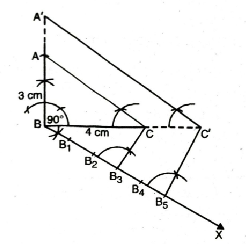
5. Through B5, draw a line parallel to BC meeting BC is c’ on being produced.
6. Again draw a line through C’ parallel to CA meeting BA is A’ on being produced. Δ’ABC’ is the required triangle whose sides are 5/3 times the sides of ΔABC.
Justification of construction :
Consider ΔA’BC’ and ΔABC
∠B = ∠B            [common]
∠A’C’B = ∠ACB         [By construction]
∴ ΔA’BC ∼ ΔABC      [AA-similarity condition]
∴ Their corresponding sides must be in the same ratio
Again, in ΔB5C’ B and ΔB3CB,
∠B = ∠B                  [common]
∠C’B5B = ∠CB3B             [By construction]
∴ ΔΒ5C’B ∼ ΔΒ3CB          [AA-similarity]
∴ Their corresponding sides must be in the same ratio

Hence the construction is justified,

Construction of Tangents

We know that if a point lies inside a circle, there cannot be a tangent to the circle through this point. However if a point lies on the circle, then there is only one tangent to the circle at this point and it is perpendicular to the radius through this point.
  • Take a point on the circle.
  • Join centre of circle and this point i.e. draw the radius of the circle through this point.
  • Draw perpendicular to the radius through this point i.e. construct a right angle (90°) at this point. The perpendicular is the tangent to the circle through this point.
Note: If centre of the circle is not given, you may locate its centre first by taking any two non-parallel chords and then finding the point of intersection of their perpendicular bisectors. Then follow the steps in steps to draw tangent at a point on the circle.

TEXT BOOK EXERCISE 11.2

In each of the following, give also the justification of the construction.

Q. 1. Draw a circle of radius 6 cm from a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. 
Solution.
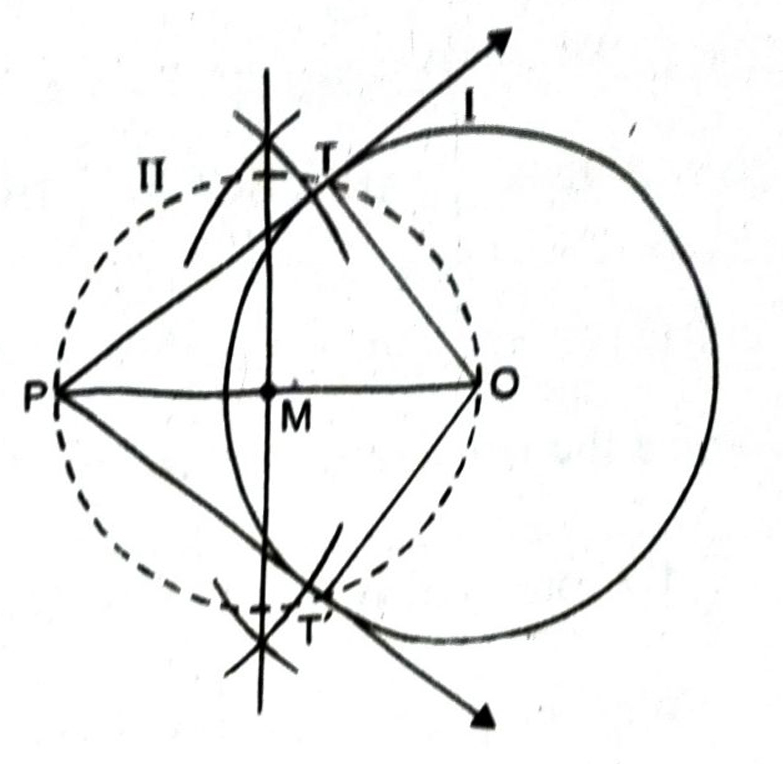
Steps of construction :
  1. Draw a circle (I) of radius 6 cm.
  2. Take a point ‘P’ at a distance of 10 m from the centre of the circle. Join OP.
  3. Draw perpendicular bisector of OP. Let ‘M’ be the mid point OP.
  4. With ‘M’ as centre and radius MO, draw a circle (II) which intersects the circle (I) at T and T’.
  5. Then PT and PT’ are two required tangents.
Justification of construction :
We know that tangent at a point is always perpendicular to the radius at the point. Now we have to prove that ∠PTO = ∠PT’O = 90°;
OT is joined.
Now, PMO is the diameter of circle (II)
and ∠PTO is in the semicircle.
∴ ∠PTO = 90°      [Angle in semicircle is a right angle]
Similarly, ∠PT’O = 90°
∴ PT and PT’ has to be the tangents to the circle at T and T’.
On measuring, the lengths of tangents
i.e., PT = 8.1 cm
       PT’ = 8.1 cm.
[Co-centric circles. Two or more circles having same centre but different radii are called CO-CENTRIC circles.]
Q. 2. Construct a tangent to a circle of radius 4 cm from a point on the co-centric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution. Steps of construction :
  1. Draw a circle with cente ‘O’ and radius 4 cm. Mark it as I.
  2. Draw another circle with same centre ‘O’ and radius 6 cm and mark it as II.
  3. Take any point ‘P’ on circle II. Join OP.
  4. Draw perpendicular bisector of OP. Let it intersects ‘OP’ at M.
  5. With M as centre and radius ‘MO’ or ‘MP’, draw a circle III which intersects the circle ‘I’ at T and T’.
  6. Join PT.
PT is the required tangent.
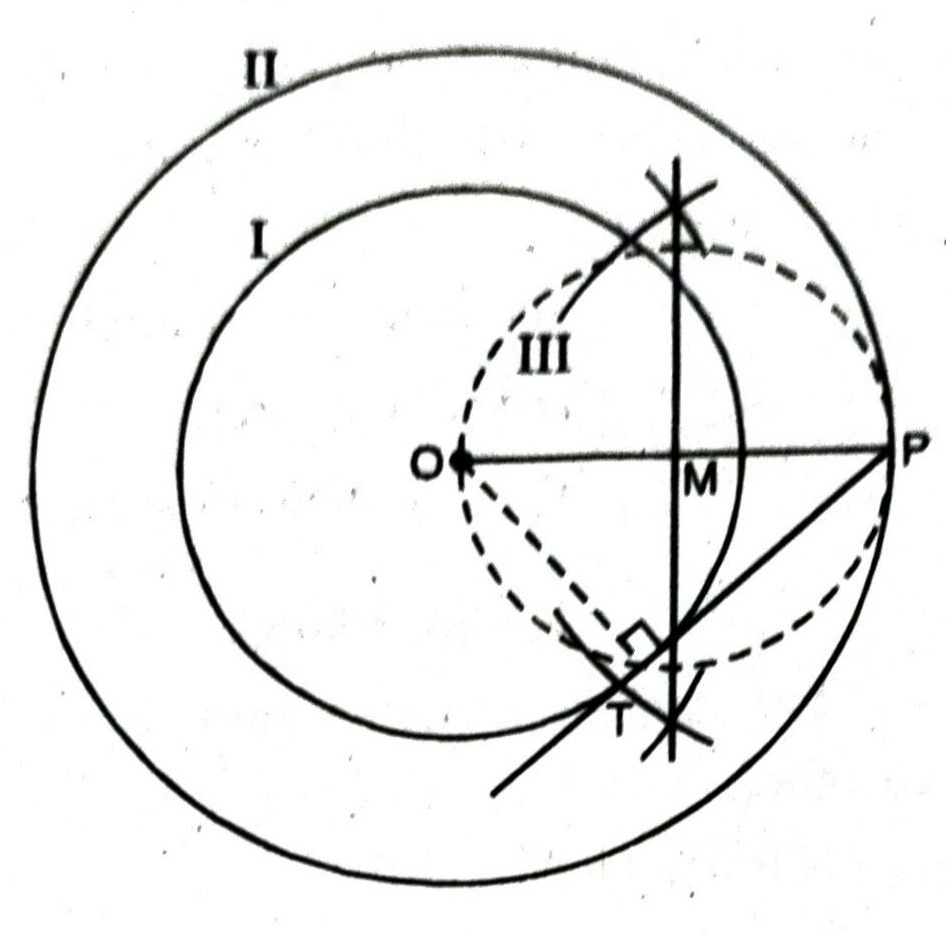
Justification of the construction :
Join OT.
Now OP is the diameter of the circle III.
∠OTP is in the semicircle.
∴ ∠OTP = 90°.                      ……(1)
[∵ Angle in a semicircle is a right angle]
Now OT ⊥ PT                     [using (1)]
∵ A line which makes an angle of 90° with radius at any point on the circle, the line is tangent to the circle.
∴ PT is tangent to the circle ‘I’
i.e., PT is tangent to the circle of radius 4.5 cm.
To calculate the length of tangent :
Consider ΔΟΤΡ,
∠OTP = 90°                  [using (i)]
∴ ΔOTP is a right angled triangle.
OT = 4 cm                 [Radius of I circle(given)]
OP = 6 cm                [Radius of the II circle (given)]
PT = ?                      [to be calculated]
In rt. triangle ΔOTP,
By Pythagoras theorem,
OP2 = OT2 + PT2       [(Hyp)2 = (Base)2 + (Perp.)2]
or      PT2 = OP2 – OT2
       = 62 – 42
       = 36 – 16 = 20
 PT = √20 cm
       = 2√5 = 2 × 2.24 = 4.48 cm.
So, length of tangent by actual calculation = 4.48 cm = 4.5 cm
Length of tangent by measurement = 4.5 cm
Hence, the length of tangent ‘PT’ is verified.
Q. 3. Draw a circle of radius 3 cm. Take two points P and Q on one of its ertended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points ‘P’ and ‘Q’.
Solution.
Steps of construction
1. Draw a circle of radius 3 cm and centre ‘O’.
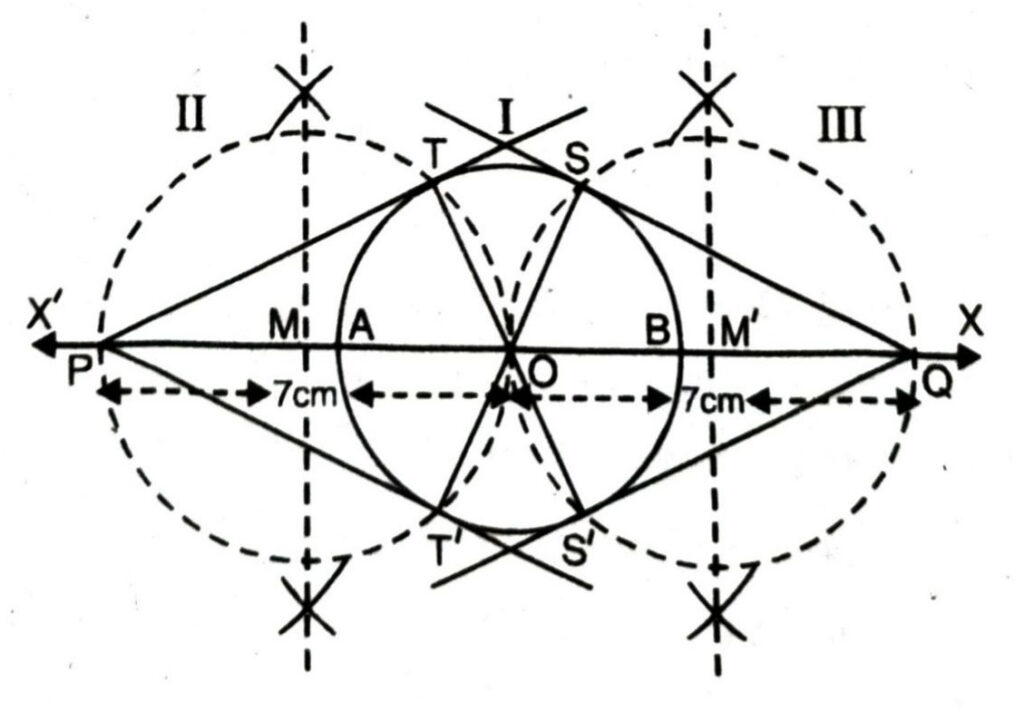
2. Draw its diameter ‘AB’ and extend it in both directions as OX and OX’.
3. Take a point ‘P’ on ‘OX” direction and ‘Q’ on ‘OX’ direction such that OP = OQ = 7 cm.
4. Draw perpendicular bisectors of OP and OQ which intersects OP and OQ at ‘M’ and ‘M” respectively.
5. With ‘M’ as centre and radius = ‘MO’ or MP, draw a circle ‘II’ which intersects the circle ‘I’ at T and T’.
6. Similarly with ‘M” as centre and radius = M’O or MQ, draw a circle (III) which intersects the circle ‘I’ at ‘S’ and ‘S’.
7. Join PT, PT’ and QS and QS’.
Justification of construction :
Join ‘OT’ and ‘OT’ and ‘OS’ and OS’.
To prove ‘PT & PT’ tangents to the circle we will prove that ∠PTO= ∠PT’O = 90°.
Now ‘OP’ acts as the diameter of circle ‘II’ and ∠OTP is in the semicircle.
∴ ∠OTP = 90°           …(1)
[∵ Angle in semicircle is 90°]
But ‘OT’ is the radius of circle ‘I’ and line ‘PT’ touches the circle at ‘T’.
∵ The line which touches the circle at a point and makes an angle of 90° with radius at that point, is tangent to the circle.
∴ PT is tangent to the circle I at point T through point ‘P’.
Similarly PT’, QS and QS’ are tangents to the circle I.
Q. 4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60° ?
Solution.
Steps of construction.
1. Draw the rough sketch of required figure.
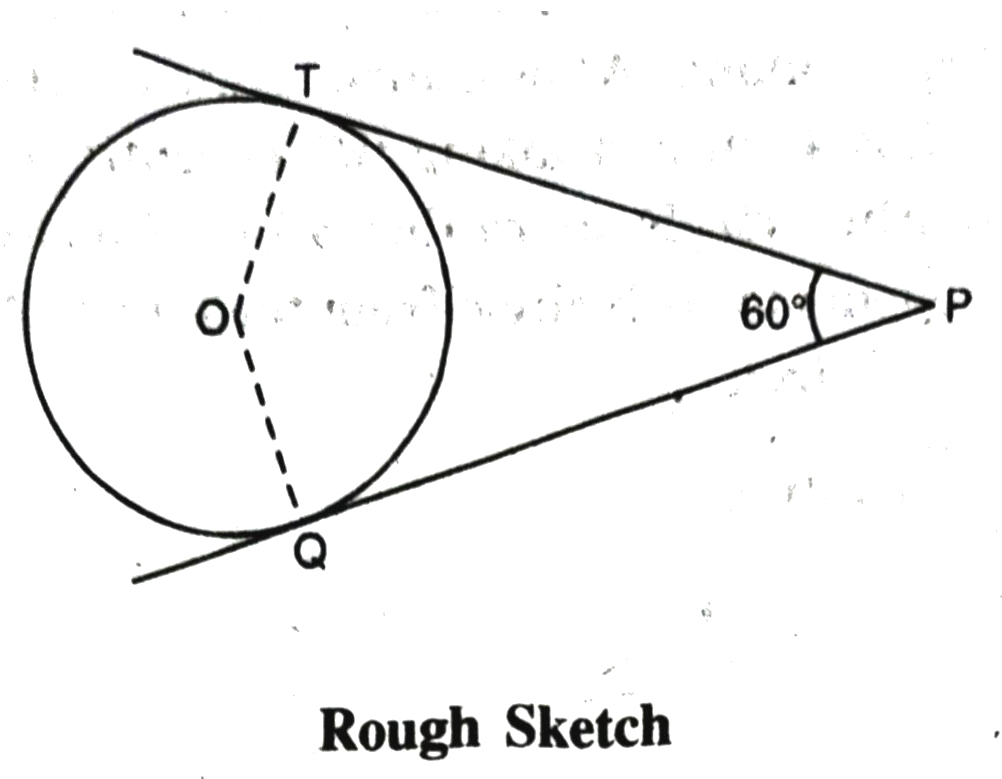
∵ the tangents make an angle of 60° with each other.
∠OTP = ∠OQT = 90°
[Tangent is perpendicular to the radius of circle]
To find inclination of radii with each other ∠TOQ + ∠OTP + ∠OQT + ∠TPQ = 360°
[Angle sum property of quad.]
or ∠TOQ + 90° + 90° + 60 = 360°
or ∠TOQ = 360 – 90° – 90° – 60° = 120°
2. Draw a circle of radius 5 cm.
3. Draw two radii of circle which make an angle of 120° with each other.
4. The radii intersect the circle at ‘A’ and ‘B.
5. Make an angle of 90° at each point A and B, which intersect each other at ‘P’
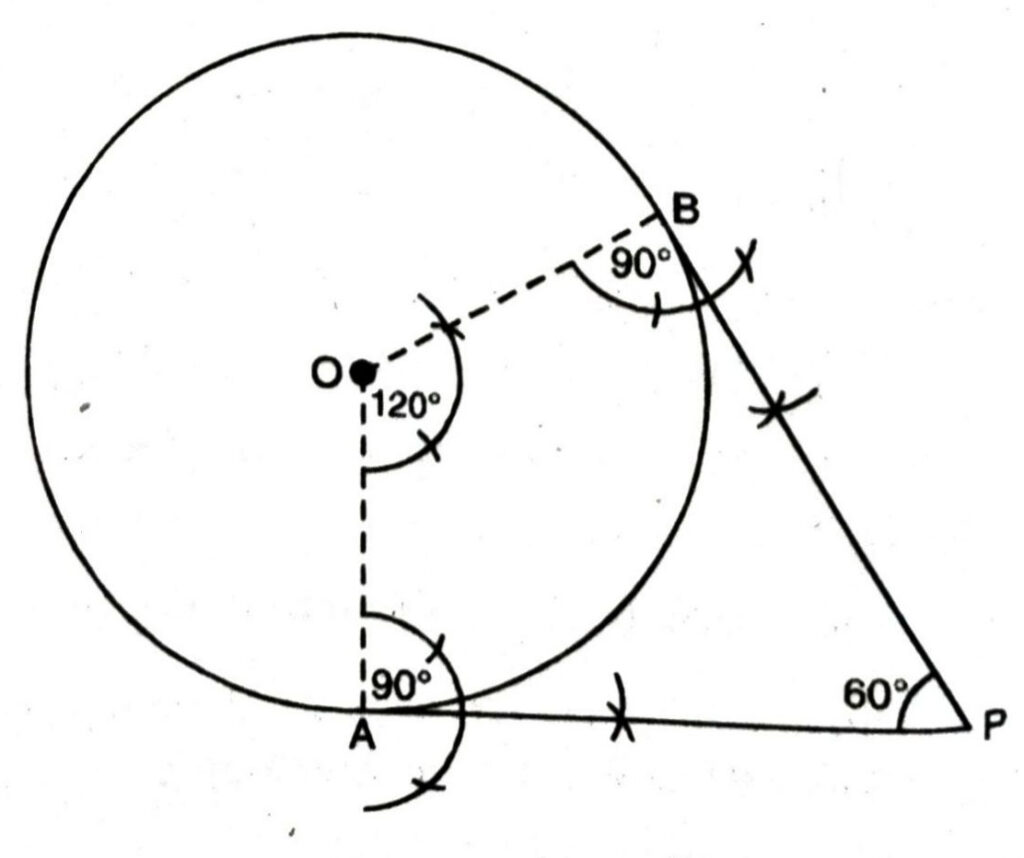
6. PA and PB are the required tangents.
Q. 5. Draw a line segment AB of length 8 cm. Taking ‘A’ as centre, draw a circle of radius 4 cm and taking ‘B’ as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution.
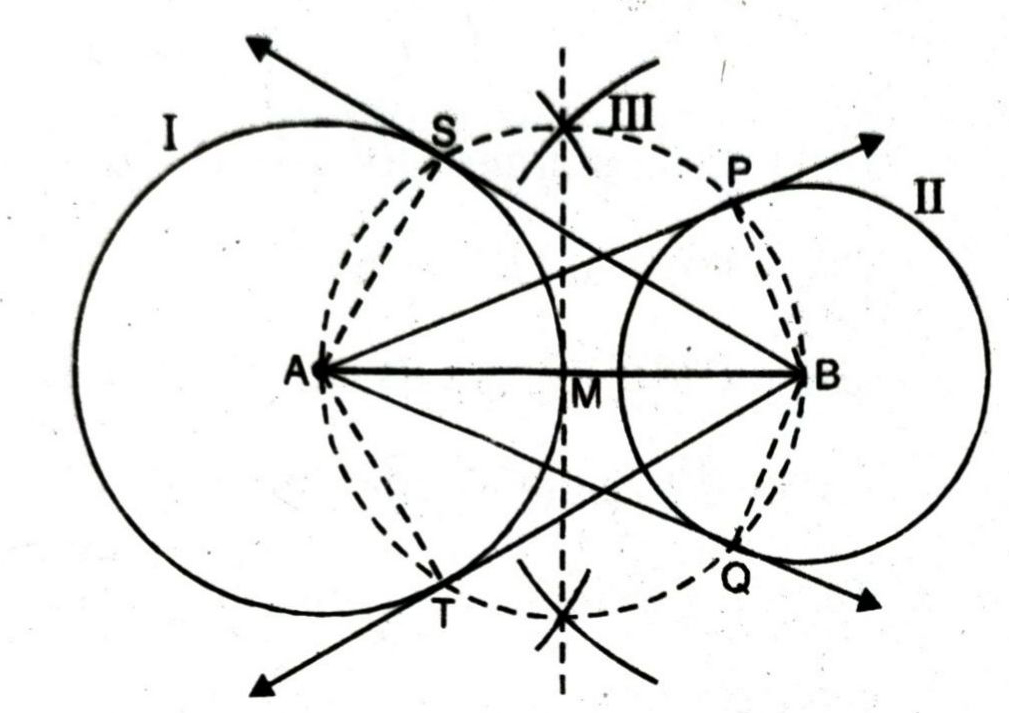
Steps of construction :
  1. Draw a line segment AB = 8 cm.
  2. With ‘A’ as centre and radius 4 a circle (I) cm, draw
  3. With ‘B’ as centre and radius 3 cm, draw a circle ‘II’.
  4. Draw the perpendicular bisector of line segment AB which intersects ‘AB’ at ‘M’.
  5. With ‘M’ as centre and radius MA or MB, draw a circle (III) which intersects the circle (1) at ‘S’ and ‘T’ and circle (II) at ‘P’ and ‘Q’.
  6. Join ‘AP’ and ‘AQ’. These are required tangents to the circle with radius 3 cm. from point ‘A’.
  7. Join ‘BS’ and ‘BT’. These are required tangents to the circle with radius 4 cm from point ‘B’.
Justification of Construction :
In circle (III), AB acts as diameter then ∠ASB and ∠BPA are in semicircle.
∴ ∠ASB = 90°      …(1) [Angle in semicircle]
and ∠BPA = 90° …(2)
But ∠ASB is angle between radius of circle (I) and line segment ‘BS’ and ∠BPA is angle between radius of circle (II) and line segment ‘AP’.
∵ Line segment which is perpendicular to the radius of circle, is tangent to the circle through that point.
∴ BS is tangent to circle (I) at point ‘S’
and AP is tangent to circle (II) at point ‘P’.
Similarly AQ and BT are tangents to the circle (II) and (I) respectively.
Q. 6. Let ABC be a right triangle in which AB= 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from ‘A’ to this circle.
Solution.
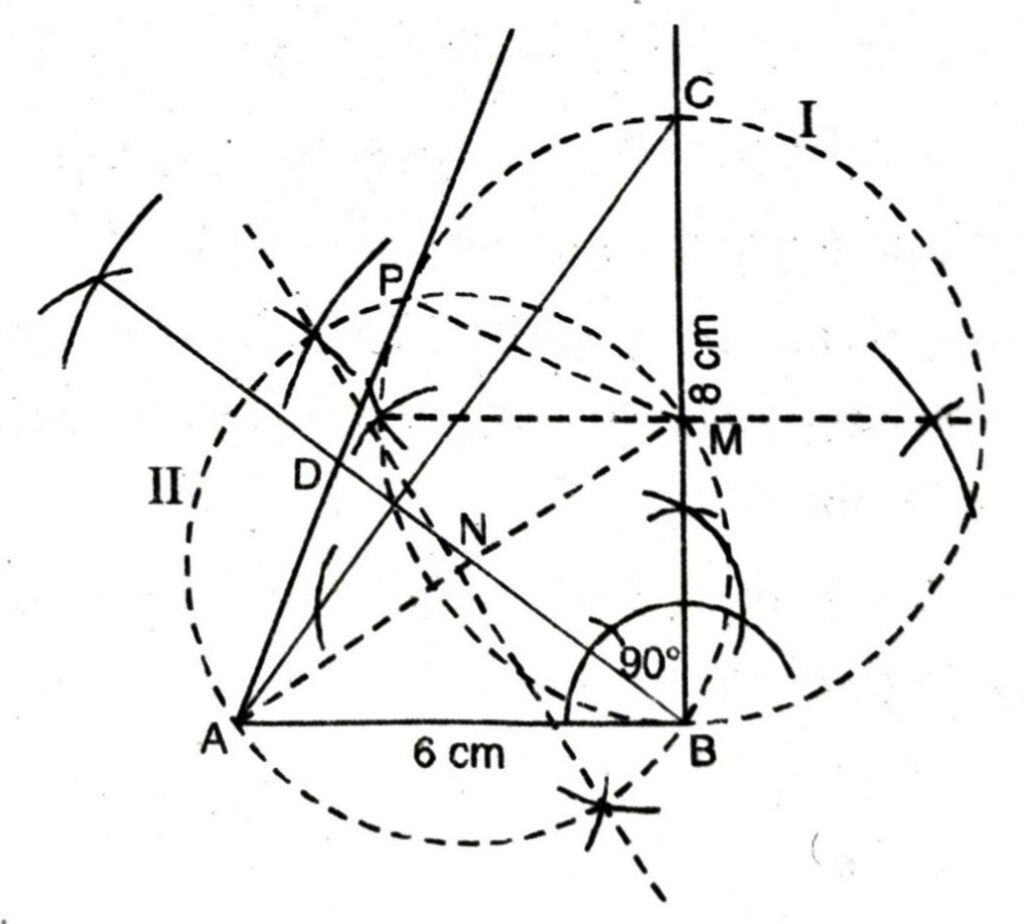
Steps of construction :
  1. Construct rt. angled triangle ABC according to given conditions and measurements.
  2. Draw BD ⊥ AC.
  3. Take mid point of side BC take it as ‘M’.
  4. Take ‘M’ as centre and BC as diameter, draw a circle through B, C, D using property, angle in semicircle is 90° (∠BDC = 90°). Take this circle as I.
  5. Now join ‘A’ and ‘M.
  6. Draw perpendicular bisector of ‘N’. Now with ‘N’ as centre and ‘NA’ or ‘NM’ as radius, draw a circle (II) which intersects the circle (I) at ‘B’ and ‘P’.
  7. Join AP.
  8. AP and AB are the required tangents.
Justification of construction
Line segment ‘AM’ is diameter of circle (II) ∠APM is in semicircle
∴ ∠APM = 90°         [Angle in semicircle]
i.e., MP ⊥ AP
But ‘MP’ is the radius of circle (I) .
∴ AP is tangent to the circle (II)
[∵ Any line to radius of circle at any point on the circle is tangent to the circle.]
Similarly ‘AB’ is tangent to circle (I). .
Q. 7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution. To draw circle with bangle means the centre of circle is unknown. First find the centre of circle.
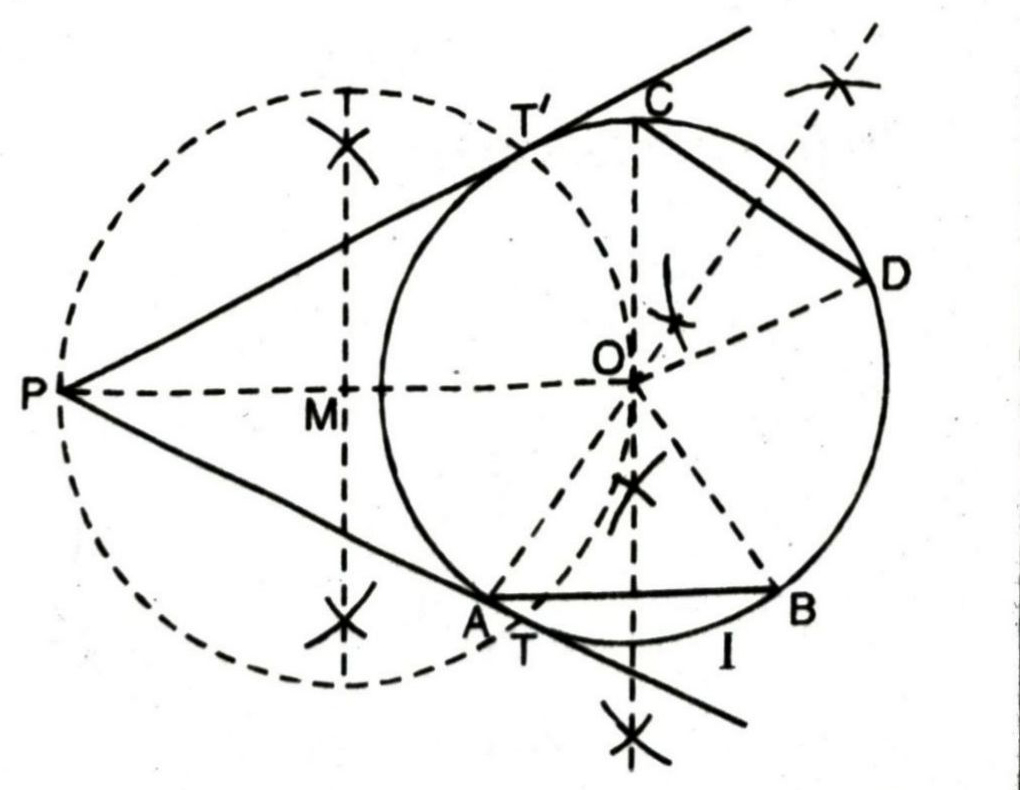
Steps of construction :
1. Draw a circle using a bangle (I).
2. Take any two chords AB and CD (nonparallel) on circle.
3. Draw the perpendicular bisectors of chords AB and CD. The perpendicular bisectors intersect each other
[∵ any point lying on perpendicular bisector of line segment is equidistant from its end points]
[∵ ‘O’ lies on 1 bisector of AB and CD]
∴ OA = OB and OC = OD
∴ OA = OB = OC = OD     (Radii of circle)
∴ ‘O’ is the centre of circle.
4. Take any point ‘P’ out side the circle.
5. Join OP.
6. Draw the perpendicular bisector of OP let ‘M’ the mid point of OP.
7. With ‘M’ as centre and radius ‘MP’ or ‘MO’, draw a circle II which intersects the circle (I) at T and T’.
8. Join PT and PT’, which is required pair of tangents.
Justification of construction :
Tangent at a point is always perpendicular to the radius at the point. Now, we have to prove that ∠PTO = PT’O = 90°.
Join OT.
Now ∠PTO is in the semicircle I.
∴ ∠PTO = 90°
[Angle in semicircle is a right angle]
Similarly ∠PTO = 90°

∴ PT and PT’ has to be the tangents to the circle at T and T’.

Follow on Facebook page – Click Here

Google News join in – Click Here

Read More Asia News – Click Here

Read More Sports News – Click Here

Read More Crypto News – Click Here

Leave a Reply

Your email address will not be published. Required fields are marked *