PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

PSEB 9th Class Maths Solutions Chapter 10 Circles Ex 10.3

Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:

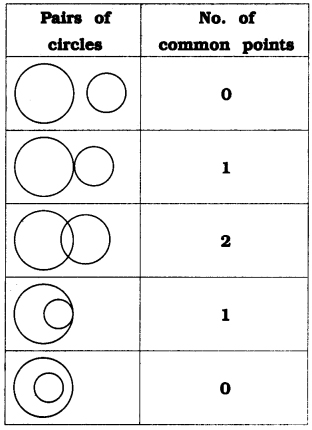
Thus, given a pair of circles, the maximum number of common points they have is 2.

Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Answer:

• In the given circle, draw chords AB and BC with one endpoint B in common.
• Draw l-the perpendicular bisector of AB and m-the perpendicular bisector of BC.
• Let l and m intersect at O.
• Then, O is the centre of the given circle.

Note: Here, any two chords without an end-point in common can be drawn.

Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:

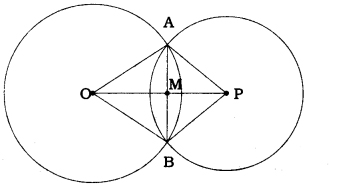
Here, two circles with centre O and P intersect each other at points A and B.
AB and OP intersect at M.
In ∆ OAP and ∆ OBR
OA = OB (Radii of the circle with centre O)
PA = PB (Radii of the circle with centre P).
OP = OP (Common)
∴ ∆ OAP ≅ ∆ OBP (SSS rule)
∴ ∠ AOP = ∠ BOP (CPCT)
∴ ∠ AOM = ∠BOM
Now, in ∆ AOM and ∆ BOM,
AO = BO (Radii of the circle)
∠ AOM = ∠ BOM
OM = OM (Common)
∴ ∆ AOM = ∆ BOM (SAS rule)
∴ AM = BM and ∠ AMO = ∠ BMO (CPCT)
But, ∠AMO + ∠BMO = 180° (Linear pair)
∴ ∠ AMO = ∠ BMO = 180°/2 = 90°
Thus, line OM is the perpendicular bisector of AB.
Hence, line OP is the perpendicular bisector of AB.
Thus, the centres O and P of the circle intersecting in points A and B lie on the perpendicular bisector of common chord AB.

Follow on Facebook page – Click Here

Google News join in – Click Here

Read More Asia News – Click Here

Read More Sports News – Click Here

Read More Crypto News – Click Here