JKBOSE 9th Class Mathematics Solutions Chapter 2 Polynomials
JKBOSE 9th Class Mathematics Solutions Chapter 2 Polynomials
JKBOSE 9th Class Mathematics Solutions Chapter 2 Polynomials
Jammu & Kashmir State Board JKBOSE 9th Class Mathematics Solutions
J&K class 9th Mathematics Polynomials Textbook Questions and Answers
Algebraic Expression. An algebraic expression is a combination of literals and numbers connected by +, -, × and ÷
For example, 3x + 7, x ÷ 1/x, x³ + y are algebraic expressions.
Polynomial. An algebraic expression in which the variables involved have only one non-negative integral exponents, is called a polynomial e.g. 5x + 9, x² + 3x, 2x² + 3x + 7, etc. are polynomials in one variable x only.
In polynomial x² + 3x the expressions x² and 3x are called the terms of the polynomial. So polynomial 2x² + 3x + 7 has three terms namely 2x², 3x and 7. Where the coefficient of x² is 2, coefficient of 3x is 3 and 7 is called the constant term.
Monomials. Polynomials having only one term are known as monomials e.g. 3x², 5x etc. are monomials.
Binomials. Polynomials having only two terms are known as binomials e.g. 4x³ + x, 5x² + 3x² etc. are binomials.
Trinomials. Polynomials having only three terms are known as trinomials. e.g. 6x5 + 3x + 7, x² + 7x + 12 etc. are trinomials.
Remark. The part poly in polynomials means many. The word meaning of polynomial signifies an algebraic expression with many terms. However it is used for monomials, binomials and trinomials also.
Degree of a polynomial in one variable. If the polynomials is in one variable then the highest exponent (power) of the variable is called the degree of the polynomial e.g. (i) 3x + 7 is a polynomial in x of degree one.
(ii) 4 + 2x + 11x² is a polynomial in x of degree two.
(iii) m4 + 2m² + 9 is a polynomial in m of degree 4.
As x0 = 1, therefore a constant is a polynomial of degree zero. The degree of the polynomial say; 4 is zero.
Linear polynomial. A polynomial of degree 1 is called a linear polynomial.
2x + 1, √3y – 1, 5 – z etc. are the examples of linear polynomial.
As a linear polynomial in x has at most two terms, we may denote it in the form ax + b, where a and b are constants and a ≠ 0.
Quadratic polynomial. A polynomial of degree 2 is called a quadratic polynomial.
7 – x², 5y + 3y², 2 – z – z² etc. are some examples of quadratic polynomial.
A quadratic polynomial in one variable will have atmost 3 terms. List few more such quadratic polynomials. We can represent a quadratic polynomial in x as ax² + bx+c, only if a ≠ 0 and a,b,c are constants. A quadratic polynomial in y may be of the form ay² + by + c provided a ≠ 0 and a, b, c are constants.
Cubic polynomial : A polynomial of degree three as a cubic polynomial. 4x³,2x³ + 1; 5x³ + x, 6 − x³,6x³ − x², 2x³ + 4x² + 6x + 7 are some examples of a cubic polynomial in x. A cubic polynomial in one variable can have atmost 4 terms. A cubic polynomial in x may be written in the form ax³ + bx² + cx + d, where a ≠ 0 and a, b, c and d are constants.
Now, we are in a position to think of a polynomial in one variable of degree n? A polynomial in x of degree n can be defined as
p(x) = a0 + a1x + a2x² + ………. anxn
Where a0, a1, a2, ……… an are constants and a ≠ 0. In particular,
if a0 = a1 = a2 = a3 = ……….. an = 0 (all the constants are zeros), the polynomial reduces to 0 which is called zero polynomial.
So far we have dealt with polynomials in one variable only. We can also have polynomials in several variables, for example x² + y² + xyz (where variables are x, y and z), p² + q² + r (where variables are p, q and r), u³+ v² (where variables are u and v), etc. we shall be studying such polynomials in detail later.
Standard form of a polynomial.
The standard form of a polynomial in one variable is that in which the terms of the polynomial are written in the decreasing order of the exponents of the variable.
e.g. polynomial 3x4 + 2x² + 9x + 11 is in its standard form.
TEXT BOOK EXERCISE – 2.1
1. Which of the following expressions are polynomials in one variable and which are not ? State reasons for your answer.
(i) 4x²-3x + 7 (ii) y² + √₂ (iii) 3√t + √2t (iv) y + 2/y (v) x10 + y3 + t50
Solution.— 4x2 – 3x + 7 is a polynomial in x because exponent of x in each of the terms is a whole number.
(ii) y² + √2 is a polynomial in y because exponent of y in each of the terms is a whole number.
(iii) 3√t + √2t is not a polynomial in t because exponent of t in the first term i.e. in 3t1/2 is 1/2 which is not a whole number.
(iv) y +2/y is not a polynomial in y because exponent of y in the second term i.e. in 2y-1 is -1.
(v) x10 + y³ + t50 is a polynomial in three variables x, y and t, because exponent of each variable is a whole number.
2. Write the coefficients of x² in each of the following :
(a) 2 + x² + x (b) 2 – x² + x³ (c) π/2 x2 + x (d) √2x – 1.
Solution.— (a) Coefficient of x² in 2 + x² + x is 1.
(b) Coefficient of x² in 2 – x² + x³ is -1.
(c) Coefficient of x² in π/2 x2 + x is π/2.
(d) Coefficient of x² in √2x – 1
i.e., in 0x² + √2x – 1 is 0.
3. Give one example each of a √2x binomial of degree 35, and of a monomial of degree 100.
Solution.— Binomial of degree 35 is 4x35 – 3 and monomial of degree 100 is √3y100
Note : We can write some more polynomials with different coefficients.
4. Write the degree of each of the following polynomials :
(a) p(x) = 5x3 + 4x2 + 7x
(b) p(y) = 4 – y2
(c) f(t) = 5t – √7
(d) f(x) = 3
Solution.— (a) Highest power term in p(x) is 5x³ and the exponent is 3. So, the degree is 3.
(b) Highest power term in p(y) is – y² and the exponent is 2. So, the degree is 2.
(c) Highest power term in f(t) is 5t and the exponent is 1. So, the degree is 1.
(d) The only term here is 3 which can be written as 3xº and so the exponent is 0. Therefore, the degree is 0.
5. Classify the following as linear, quadratic and cubic polynomials :
(i) x2 + x (ii) x – x3 (iii) y + y2 + 4 (iv) 1 + x (v) 3t (vi) r2 (vii) 7x3 .
Solution.— (i) The polynomial x2 + x is of degree 2. Therefore it is a quadratic polynomial.
(ii) The polynomial x – x³ is of degree 3. Therefore it is a cubic polynomial.
(iii) The polynomial y + y² + 4 is of degree 2. Therefore it is a quadratic polynomial.
(iv) Polynomial 1 + x is of degree 1. Therefore it is a linear polynomial.
(v) 3t is a polynomial of degree 1. Therefore it is a linear polynomial.
(vi) r2 is a polynomial of degree 2. Therefore it is a quadratic polynomial.
(vii) 7x³ is a polynomial of degree 3. Therefore, it is a cubic polynomial.
ZEROES OF A POLYNOMIAL
Consider the polynomial
p(x) = 5x³ – 2x² + 3x – 2
If we replace x by 1 everywhere in the above polynomial, we get
p(1) = 5x (1)³ – 2(1)² + 3(1) – 2
= 5 – 2 + 3 – 2
= 4
We say that the value of p(x) at x = 1 is 4 and is denoted by p (1).
Similarly, p(0) = 5(0)3 – 2(0)² + 3(0) – 2
= -2
Consider the polynomials
p(x) = x – 1,
q(x) = x – 2 and f(x) = x.
What is p(1) ? Note that p(1) = 1 – 1 = 0.
Can you say when q(x) = 0 ?
Yes, q(2) = 0. Do you see f(0) = 0 ?
As p(1) = 0, we say 1 is the zero of the polynomial p(x) = x – 1.
The above fact is stated as follows :
The number which when replaced for the variable makes value of the polynomial zero is called a zero of the polynomial.
You must have observed that the zero of the polynomial x – 1 obtained by equating p(x) to 0 i.e. x-1=0 or x = 1. We say p(x) = 0 is a polynomial equation and 1 is the root of the polynomial equation p(x) = 0. So we say 1 is the zero of the polynomial x – 1 or root of the polynomial equation x-1=0. Consider p(x) = 5. Can you tell what is its zero? It has no zero. In fact, a constant polynomial has no zero. What about the zero of the polynomial p(x) = 0 ? It is said that every real number is a zero of the zero polynomial.
Remark : If p(x) = ax + b is a linear polynomial, can we find a zero for this p(x) ? Let us try. As finding zero of the polynomial p(x) amounts to solve the polynomial equation p(x) = 0, we have
ax + b =, a ≠ 0
or, ax = -b
or, x = -b/a
Do you see that -b/a is unique ? Yes, because for a given value b of b and a non-zero value of a, -b/a is always uniqe.
Let us now list our observations :
1. Zero of a polynomial need not be zero.
2.0 may be a zero of a polynomial.
3. Every linear polynomial has a unique zero.
4. A polynomial may have more than one zero.
TEXT BOOK EXERCISE – 2.2
1. Find the value of the polynomial 5x − 4x² + 3 at
(i) x = 0 (ii) x = -1 (iii) x = 2.
Solution.— (i) The value of polynomial
p(x) = 5x – 4x² + 3 at x = 0 is given by
= 5(0) − 4(0)² + 3
= 0 – 0 +3
= 3
(ii) The value of polynomial
p(x) = 5x – 4x² +3 at x = -1 is given by
= 5 ( − 1) – 4 ( −1)² + 3
= – 5 – 4 + 3
= -6
(iii) The value of polynomial
p(x) = 5x – 4x² + 3
at, x = 2 is given by
= 5(2) – 4(2)² + 3
= 10 – 4 × 4 + 3
= 10 – 6 + 3
= -3
2. Find p (0), p(1) and p(2) for each of the following polynomials :
(i) p(y) = y² – y + 1
(ii) p(t) = 2 + t + 2t² – t³
(iii) p(x) = x³
(iv) p(x) = (x – 1) (x + 1)
Solution.—
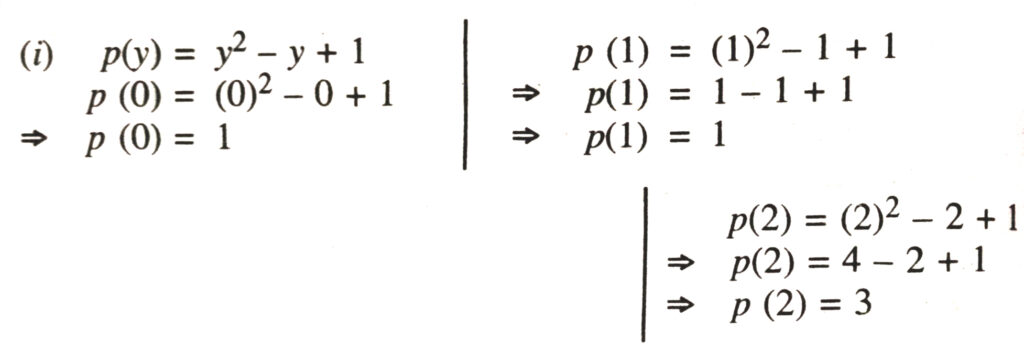
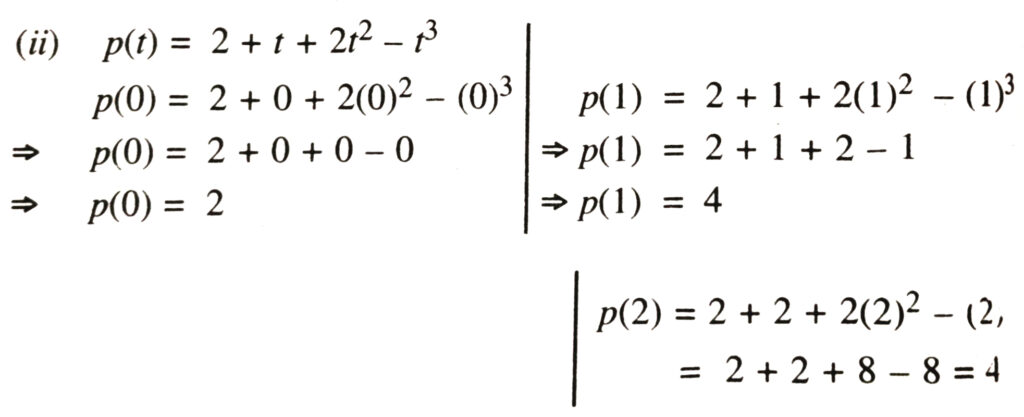
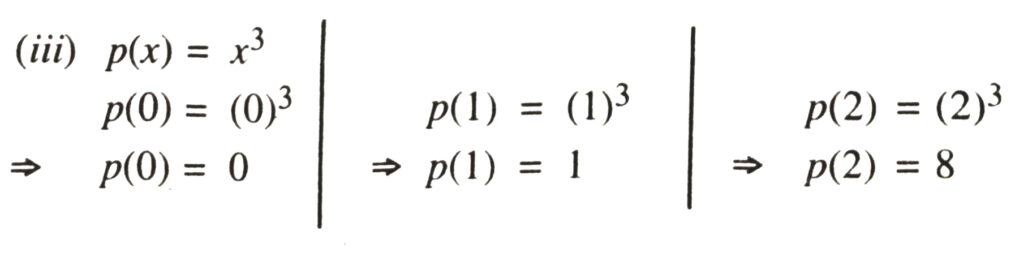
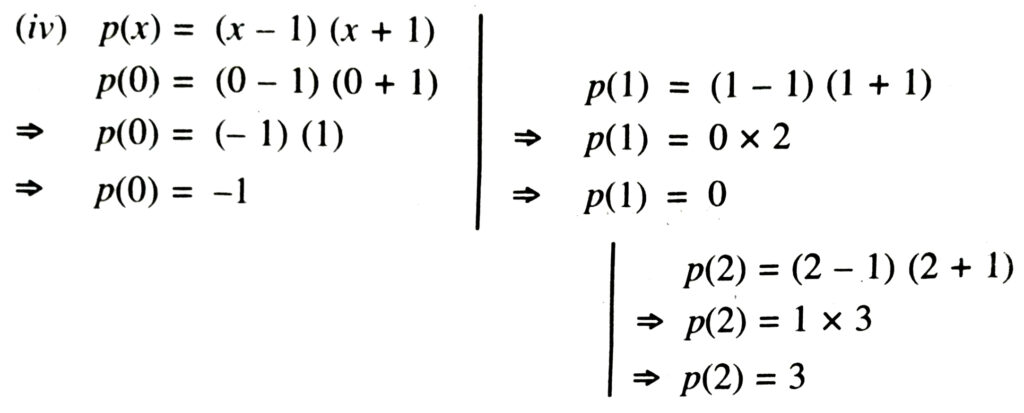
3. Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x) = 3x + 1, x = -1/3
(ii) p(x) = 5x – π, x = 4/5
(iii) p(x) = x – 1, x = 1, -1
(iv) p(x) = (x + 1) (x – 2), x = -1, 2
(v) p(x) = x2 , x = 0
Solution.— (i) Here p(x) = 3x + 1
Substitute x = -1/3 in given polynomial
So, p {-1/3} = 3 × {-1/3} + 1 = -1 +1
⇒ p{-1/3} = 0
It is verified that -1/3 is a zero of the polynomial 3x + 1.
(ii) Here p(x) = 5x – л
Substitute x = 4/5 in given polynomial
So, p{4/5} = 5 × 4/5 – π = 4 – π
⇒ p{4/5} ≠ 0
Therefore it is verified that x = 4/5 is not a zero of the polynomial 5x – π.
(iii) Here p(x) = x² −1
Substitute x = 1 in the given polynomial
So, p(1) = (1)² – 1
= 1 – 1
⇒ p(1) = 0
Therefore x = 1 is the zero of the polynomial x² – 1. Now substitute x = -1, in the given polynomial.
So, p(-1)= (-1)² – 1
= 1 – 1
⇒ P(-1) = 0
Therefore, x = -1 is the zero of the polynomial x² – 1.
(iv) Here p(x)= (x + 1) (x − 2)
Substitute x = -1 in p(x)
So, p(-1)= ( − 1 + 1) (− 1 − 2)
= 0 (-3)
= 0
Therefore it is verified that x = – 1
is the zero of the polynomial
(x + 1) (x – 2)
Now substitute x = 2 in p(x)
So, p(2) = (2 + 1) (2 – 2) = 3 × 0
⇒ p(2) = 0
Therefore it is verified that x 2 is the zero of the polynomial (x + 1)(x – 2)
(v) Here p(x) = x²
Substitute x = 0 in p(x)
So, P(0) = (0)2
⇒ p(0) = 0
Therefore it is verified that x = 0 is the zero of the polynomial x².
4. Find the zero of the polynomial in each of the following cases :
(i) p(x) = x + 5
(ii) p(x) = x – 5
(iii) p(x) = 2x + 5
(iv) p(x) = 3x – 2
(v) p(x) = 3x
(vi) p(x) = ax, a ≠ 0
(vii) p(x) = cx + d, c ≠ 0, c, d are real numbers.
Solution.— (i) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0,
We have x + 5 = 0
⇒ x = -5
So, -5 is the zero of the polynomial x + 5
(ii) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0
We have x – 5 = 0
⇒ x = 5
So, 5 is the zero of the polynomial x – 5.
(iii) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have 2x + 5 = 0
⇒ 2x = -5
⇒ x = -5/2
So, -5/2 is the zero of the polynomial 2x + 5.
(iv) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have 3x – 2 = 0
⇒3x = 2
⇒ x = 2/3
So, 2/3 is the zero of the polynomial 3x – 2.
(v) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have 3x = 0
⇒ x = 0/3
⇒ x = 0
So, 0 is the zero (root) of the polynomial 3x.
(vi) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0.
We have ax = 0
⇒ x = 0/a
⇒ x = 0
So, 0 is the zero (root) of the polynomial ax.
(vii) As finding the zero of the polynomial p(x) amounts to solve the equation p(x) = 0
We have cx + d = 0
where c ≠ 0, c, d are real numbers
⇒ cx = -d
⇒ x = -d/c
So, -d/c is the zero of the polynomial cx + d.
REMAINDER THEOREM
Remainder Theorem. Remainder theorem gives a method to find the remainder without actual division, when a polynomial p(x) with degree ≥ 1, is divided by a binomial of the form (x – a).
Must Remember. If p(x) is a polynomial, then p(x) is the remainder when p(x) is divided by (x − a).
1. If p(x) is divided by x + a, the remainder is p( − a).
2. If p(x) is divided by ax + b, then remainder is P {-b/a} :
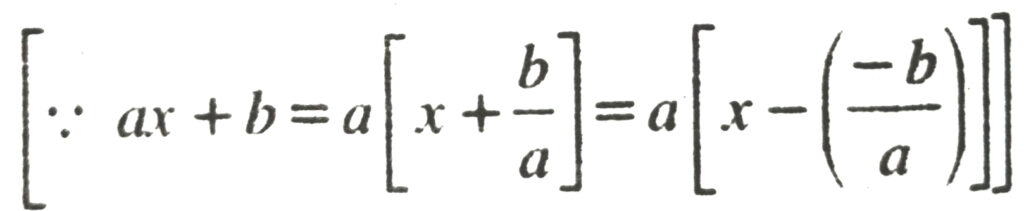
TEXT BOOK EXERCISE – 2.3
1. Find the remainder when x³ + 3x² + 3x + 1 is divided by :
(i) x + 1
(ii) x – 1/2
(iii) x
(iv) x + π
Solution.— (i) Let p(x) be x³ + 3x² + 3x + 1 and divisor is x + 1.
Remainder by long division method is as follows :
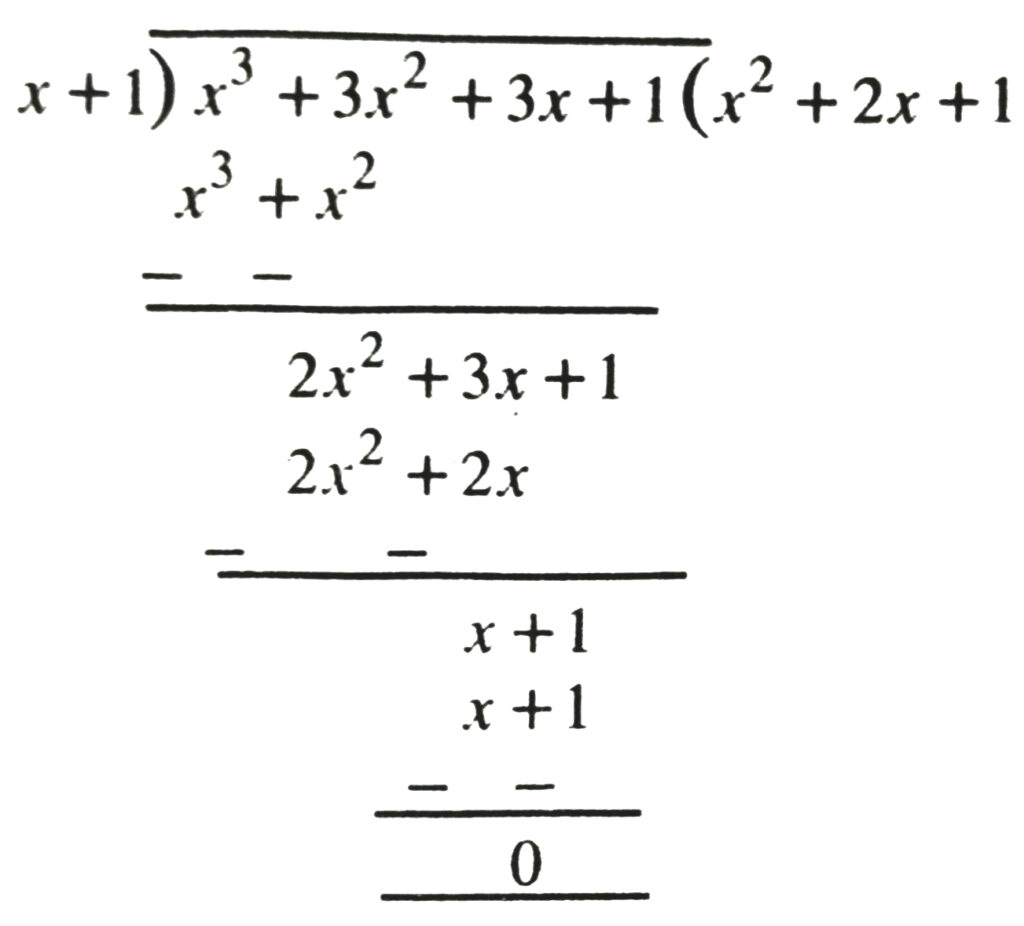
Here remainder is 0.
ALTER. Finding of Remainder by using remainder theorem.
Let p (x) = x³ + 3x² + 3x + 1
Divisor is x + 1
Now take x + 1 = 0
⇒ x = -1
Put, x = 1 in p(x) we get :
p( − 1) = (-1)³ + 3 (−1)² + 3(− 1) + 1
= −1 + 3 – 3 + 1
⇒ p(-1) = 0
Hence remainder is 0.
(ii) Let p(x) = x³ + 3x² + 3x + 1
Here divisor is x -1/2
We find the remainder by using remainder theorem.
So, take x -1/2 = 0
⇒ x = 1/2
Now put x = 1/2 in p(x) we get :
p{1/2} = {1/2}3 + 3 {1/2} + 1
= 1/8 + 3 × 1/4 + 3/2 + 1
= 1/8 + 3/4 + 3/2 + 1
= 1 + 6 + 12 + 8/8
= 27/8
Hence remainder is 27/8.
(iii) Let p(x) = x³ + 3x² + 3x + 1
Here divisor is x
We find the remainder by using remainder theorem
So take x = 0
Put x = 0 in p(x) we get :
p (0) = (0)³ + 3(0)² + 3(0) + 1
= 0 + 0 + 0 + 1
⇒ p(0) = 1
Hence remainder is 1.
(iv) Let p(x) = x³ + 3x² + 3x + 1
Here divisor is x + л.
We find the remainder by using remainder theorem.
So, take x + π = 0
⇒ x = -π
Now put x = -л in p(x) we get :
p(π) = (-π)3 + 3(-π)2 + 3(-π) + 1
= -π3 + 3π2 – 3π + 1
2. Find the remainder when x³ – ax² + 6x − a is divided by x – a.
Solution.— Let p(x) = x³ – ax² + 6x – a
Divisor is x – a
Now table x – a = 0
⇒ x = a
Put x = a in p(x), we get :
p(a) = a³ a(a)² + 6a – a
= a3 – a3 + 6a – a
= 5a
⇒ p(a) = 5a
Hence remaninder is 5a.
3. Check whether 7 + 3x is a factor of 3x3 + 7x.
Solution.— we will check it by remainder theorem.
Let, p(x) = 3x³ + 7x
Divisor is 7+ 3x
Now take 7 + 3x = 0
⇒ x = -7/3
Put x = -7/3 in p(x), we get :
Since remainder is not zero. So, 7 + 3x is not a factor 3x³ + 7x.
Factor Theorem. If the given polynomial is completely divisible by given divisor, then there is no remainder and it means that the divisor is a factor of the given polynomial.
Let p (x) be a polynomial of degree n > 1 and ‘a’ be the real number, then (x – a) is a factor of p (x) if p (a) = 0 i.e.
(i) If (x – a) is a factor of p (x), then p (a) = 0.
(ii) If p (a) = 0, then (x − a) is a factor of p (x).
Remark. In case degree of p (x) is 1, we see that as degree of p (x) = degree of (x – a) + degree of g (x)
or, 1 = 1 + degree of g (x)
or, degree of g (x) = 0
or, g (x) is a constant polynomial.
So, the factor theorem holds good even if degree of p (x) = 1.
TEXT BOOK EXERCISE – 2.4
1. Determine which of the following polynomials has x + 1 factor :
(i) x³ + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² -(2 + √2) x + √2 .
Solution.— (i) Let p (x) = x³ + x² + x + 1
Put x = -1 in p (x) we get :
p(-1) = (-1)³ + (-1)² + (-1) + 1
= -1 + 1 – 1 + 1
= 0
Hence by factor theorem x + 1 is a factor of x³ + x² + x + 1 .
(ii) Let p (x) = 4⁴ + x³ + x² + x + 1
Put x = -1 in p(x) ; we get :
p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
= 1 – 1 + 1 – 1 + 1
= 1 ≠ 0
Hence by factor theorem x + 1 is not a factor of x⁴ + x³ + x² + x + 1.
(iii) Let p (x) = x⁴ + 3x³ + 3x² + x + 1
Put x = -1 in p (x) we get :
p(-1) = (-1)⁴ + 3(-1)³ + 3 (-1)² + (-1) + 1
= 1 – 3 + 3 – 1 + 1
= 1 ≠ 0
Hence by factor theorem, x + 1 is not a factor of x⁴ + 3x³ + 3x² + x + 1.
(iv) x³ – x² – (2 + √2) x + √2
Put x = -1 in p (x) we get :
p(-1) = (-1)² – (2 + √2) (-1) + √2
= -1 – 1 + 2 √2 + √2
= 2√2 ≠ 0
Hence by factor theorem x + 1 is not a factor of x³ – x² – (2 + √2) x + √2.
2. Use the factor theorem to determine whether g (x) is a facto of p (x) in each of the following cases :
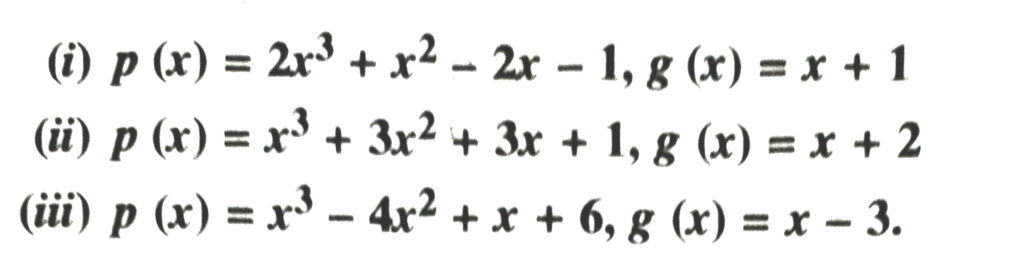

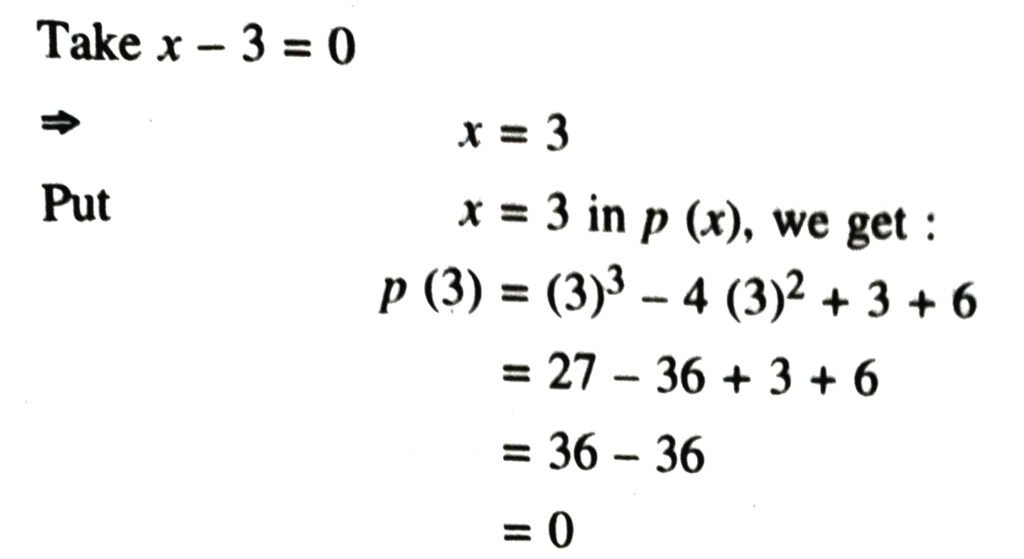
Hence by factor theorem, x – 3, i.e. g (x) is a factor of x3 – 4x2 + x + 6.
3. Find the value of k, if x – 1 is a factor of p(x) each of the following cases :
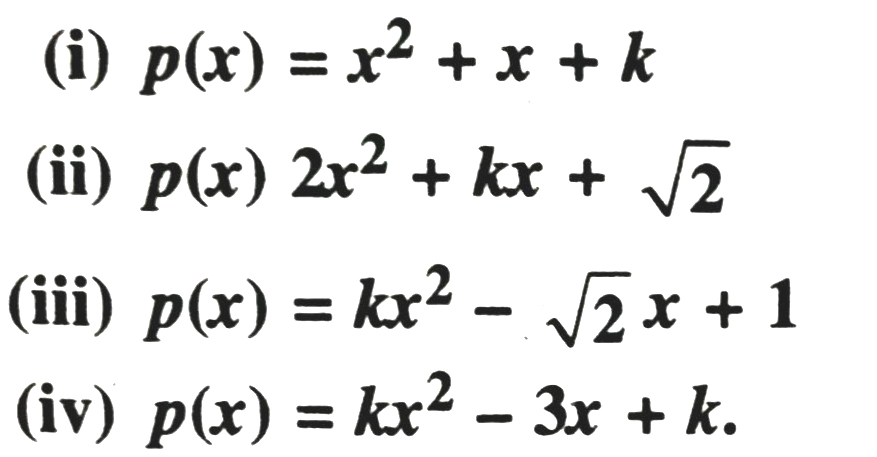
Solution.— (i) As x – 1 is a factor of
p(x) = x2 + x + k
∴ By factor theorem, p (1) = 0
⇒ (1)2 + 1 + k = 0
⇒ 1 + 1 + k = 0
⇒ 2 + k = 0
⇒ k = -2
(ii) As x – 1 is a factor of
p (x) = 2x2 + kx + √2
∴ By factor theorem, p (1) = 0
⇒ 2(1)2 + K (1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = -2 – √2
⇒ k = -(2 + √2)
(iii) As x – 1 is a factor of
p(x) = kx2 – √2x + 1
∴ By factor theorem;
p(1) = 0
⇒ k (1)2 – √2 + 1 = 0
⇒ k – √2 + 1 = 0
⇒ k = √2 – 1
(iv) As x – 1 is a factor of
p (x) = kx2 – 3x + k
∴ By factor theorem;
p (1) = 0
⇒ k (1)2 – 3 (1) + k = 0
⇒ k – 3 + k = 0
⇒ 2k = 3
⇒ k = 3/2.
4. Factories :
(i) 12x2 – 7x + 1
(ii) 2x2 + 7x + 3
(iii) 6x2 + 5x – 6
(iv) 3x2 – x – 4

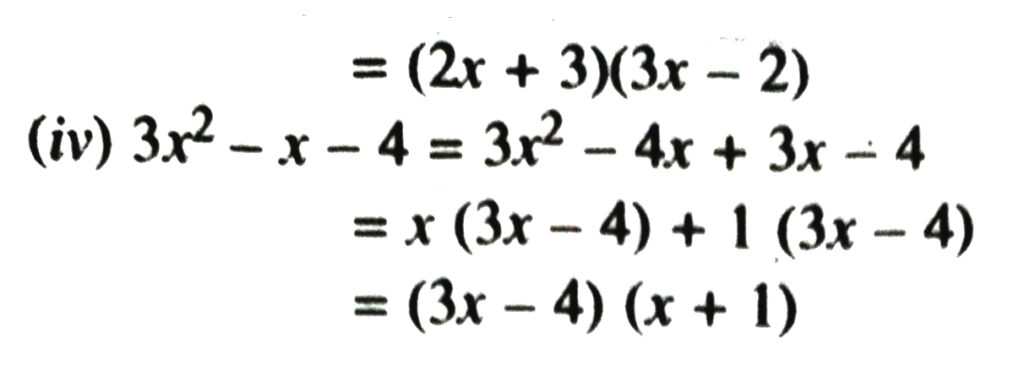
5. Factorise :
(i) x³− 2x² − x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1.
Solution.—

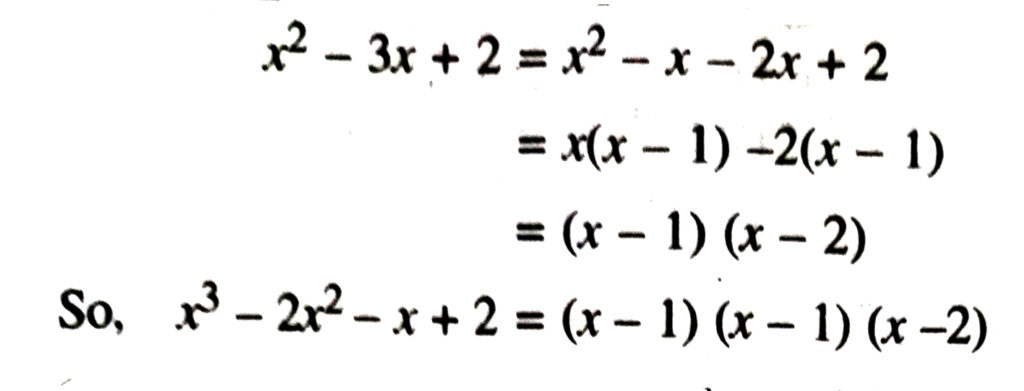
(ii) Let us denote the given polynomial as

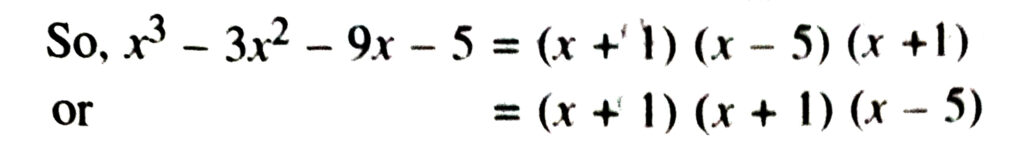
(iii) Let us denote the given polynomial as

Algebraic Identity.
An algebraic relation of equality that remains true for all values of the literals occurring in the relation is called an algebraic identity. In previous class you studied the following algebraic identities :
(a + b)² = a² + 2ab + b²
(a − b)² = a² – 2ab + b²
(a + b) (a − b) = a² – b²
Factor. When we write an algebraic expression as a product, then each expression in the product is called a factor. The process of finding factors is called factorisation.
In the chapter, we shall learn some more identities and use these identities in factorising algebraic expressions.
SOME MORE STANDARD IDENTITIES
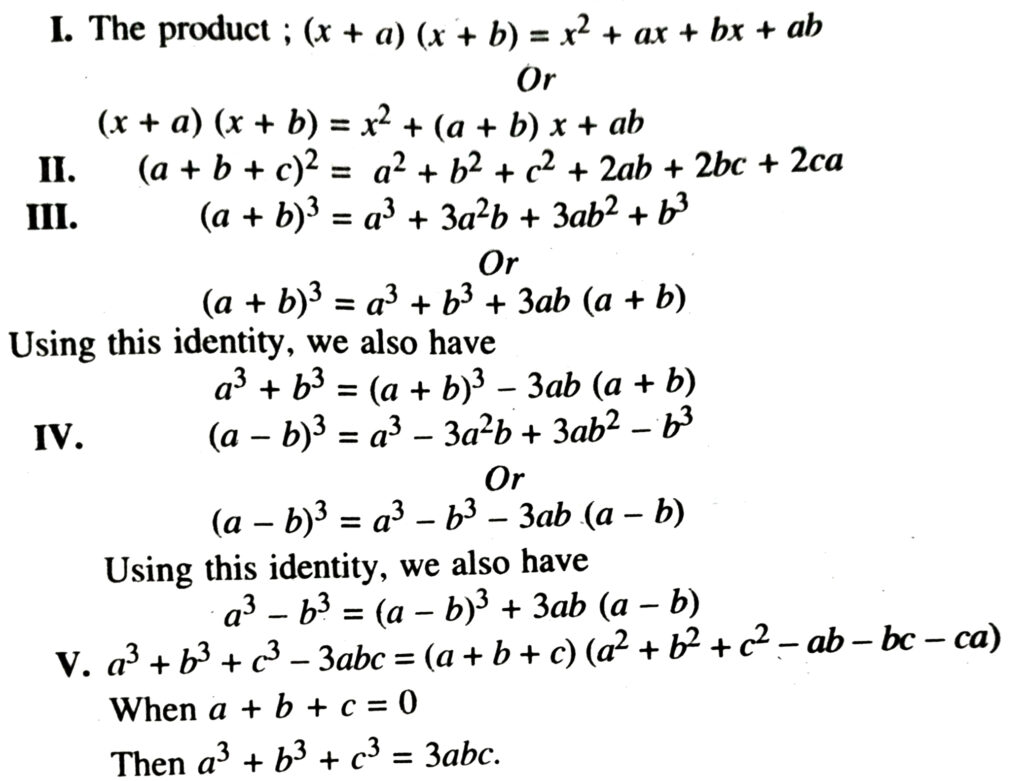
TEXT BOOK EXERCISE – 2.5
1. Use suitable identities to find the following products :
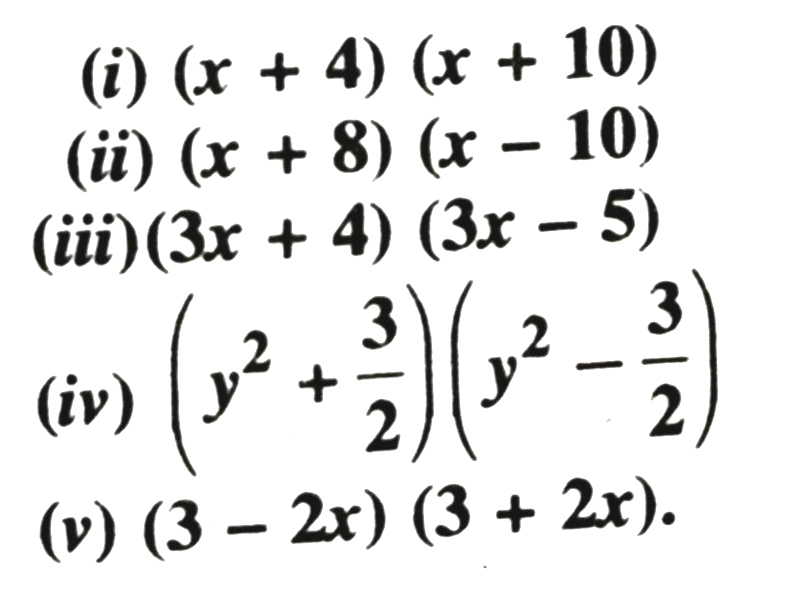
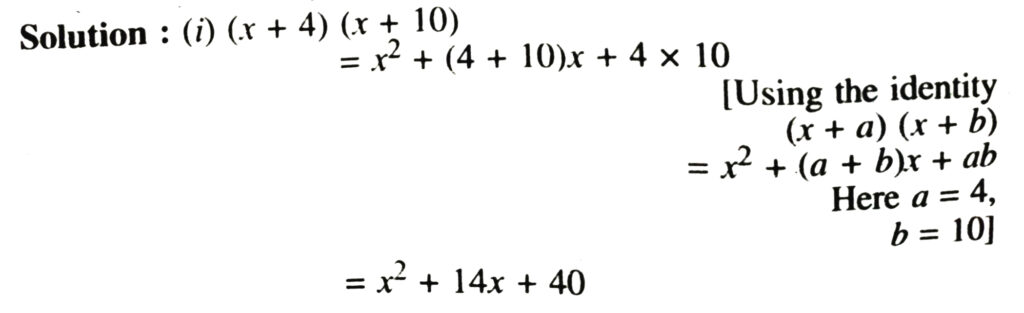


2. Evaluate the following products without multiplying directly :
(i) 103 × 107
(ii) 95 × 96
(iii) 104 × 96.

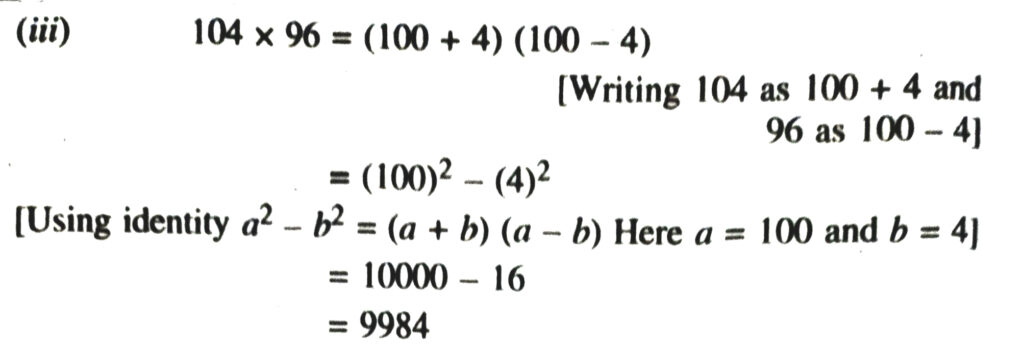
3. Factorise the following using appropriate identities :
(i) 9x² + 6xy + y²
(ii) 4y² – 4y + 1
(iii) x² – y²/100.

4. Expand each of the following using suitable Identities :
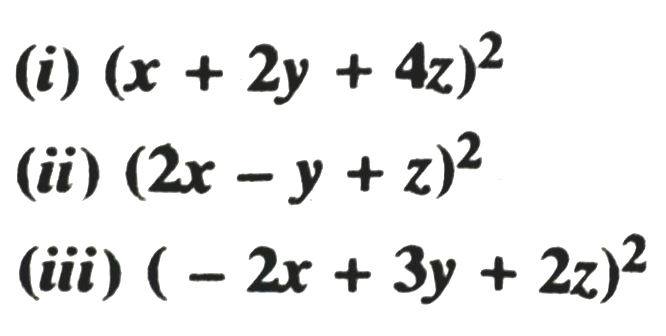
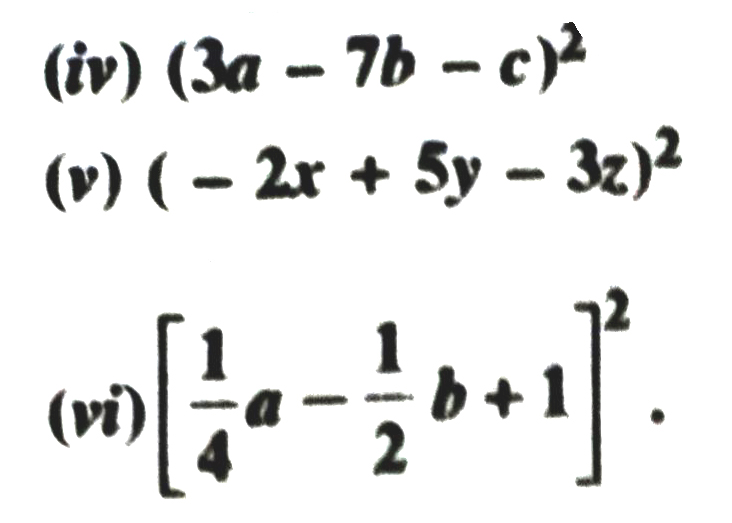

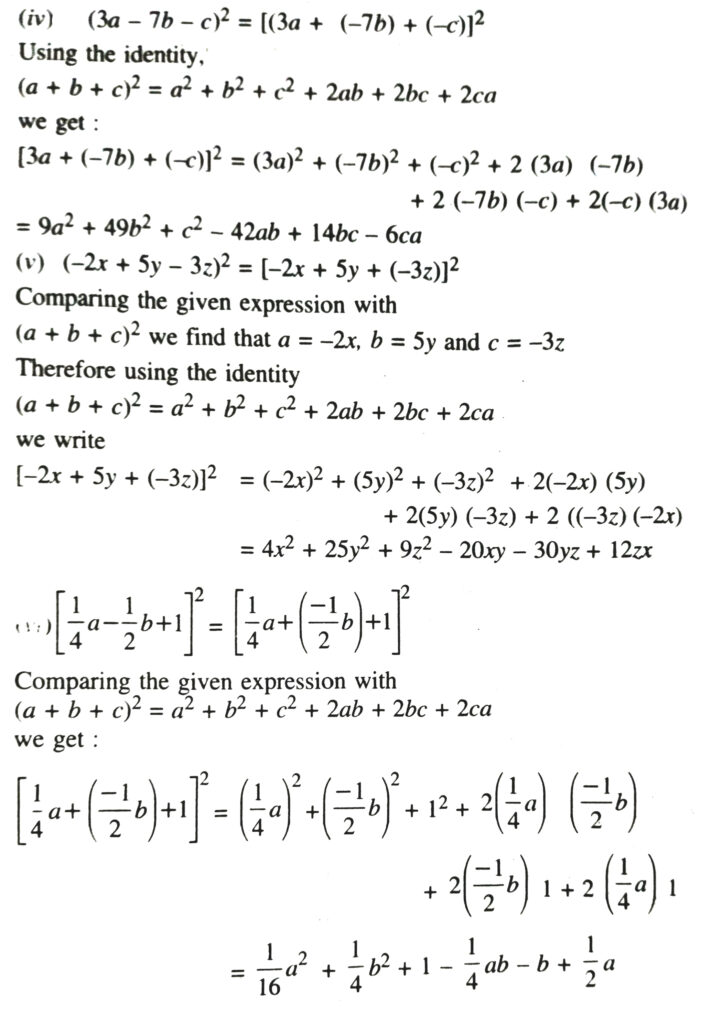
5. Factorise :
(i) 4x² + 9y² + 16z² + 12xy – 24yz − 16xz
(ii) 2x² + y² + 8z² − 2√2xy + 4√2yz – 8xz.

6. Write the following cubes in expanded form :

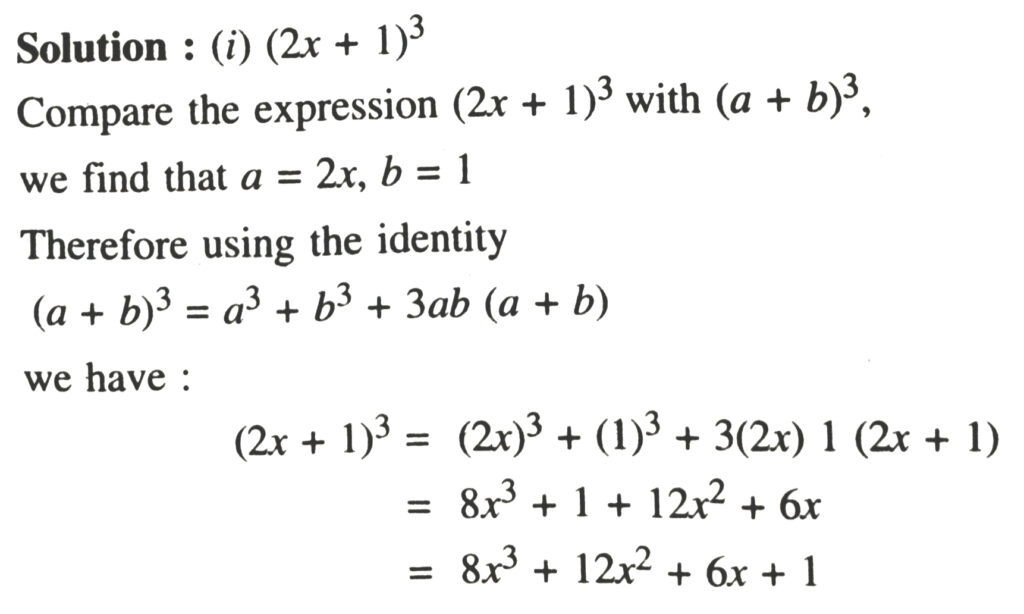
Rearranging in descending power of x
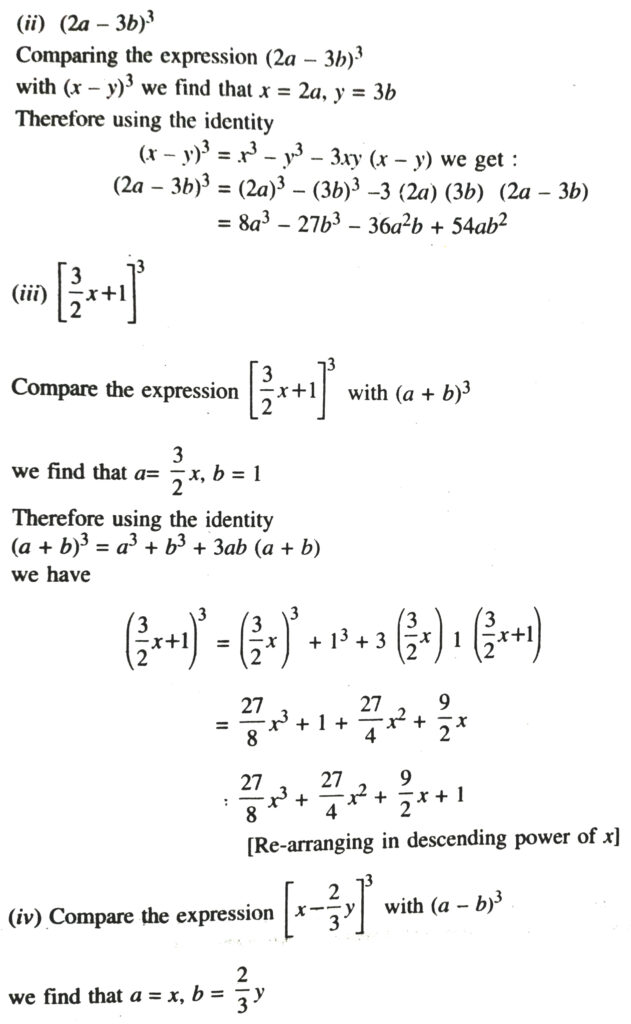

7. Evaluate the following using suitable identity :
(i) (99)³ (ii) (102)³ (iii) (998)³

8. Factorise each of the following :
(i) 8a³ + b³ + 12a²b + 6ab²
(ii) 8a³-b³-12a²b + 6ab²
(iii) 27-125a³- 135a + 225a²
(iv) 64a³ -27b3 – 144a2b + 108ab²
(v) 27p³ – 1/216 – 9/2 p2 + 1/4 p

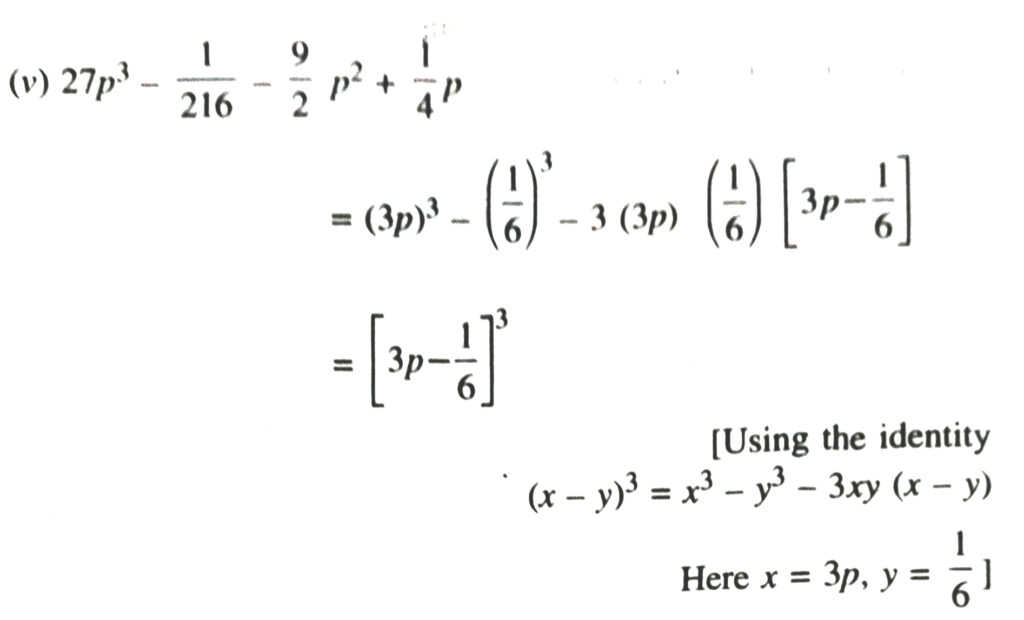
9. Verify :
(i) x3 + y3 = (x + y) (x2 – xy + y2)
(ii) x3 – y3 = (x – y) (x2 + xy + y2)

10. Factorise each of the following :
(i) 27y³ + 125z³
(ii) 64m³ – 343n³
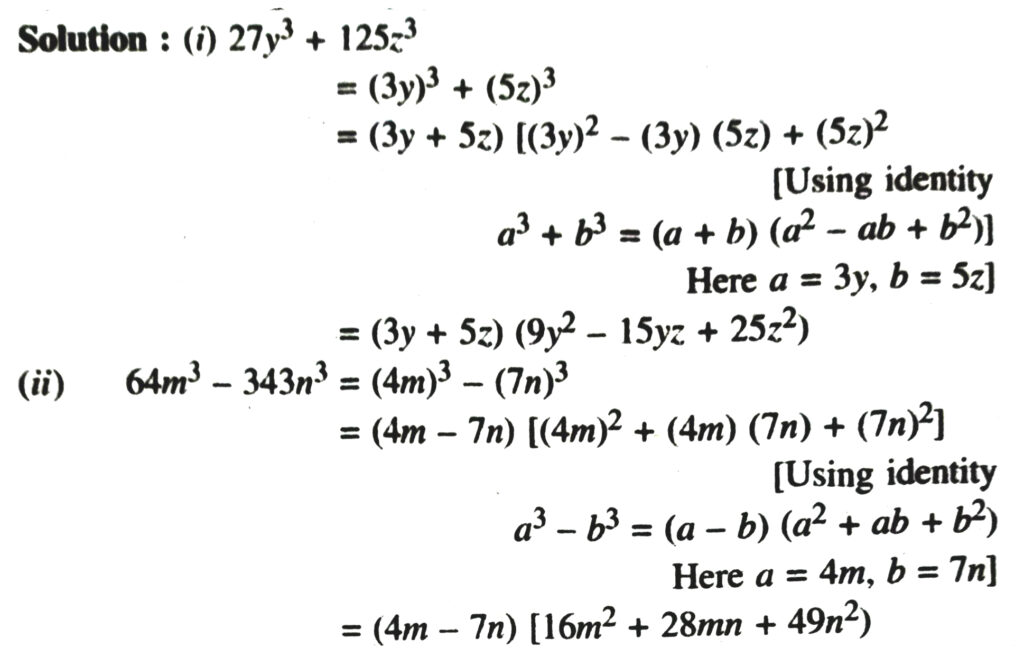
11. Factorise : 27x³ + y³ + z³ – 9xyz.
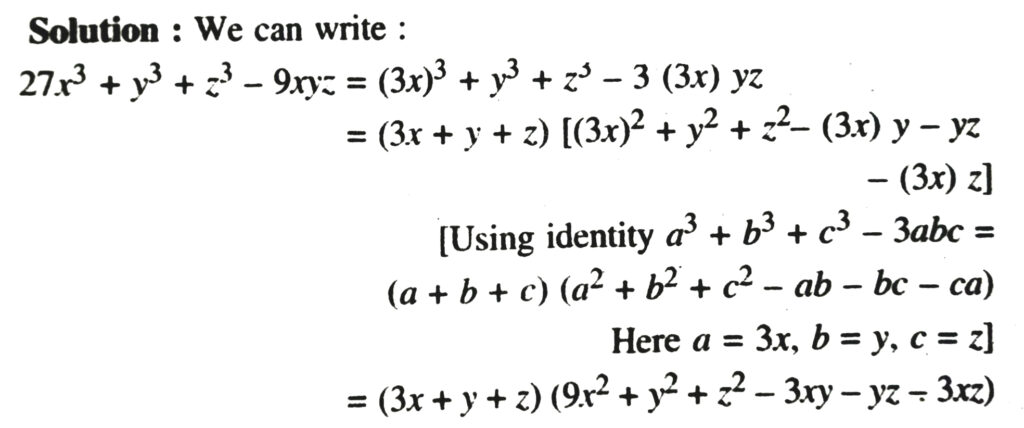
12. Verify that x³ + y³ + z³ – 3xyz = 1/2 (x + y + z) [(x – y)² + (y – z)² + (z – x)²]
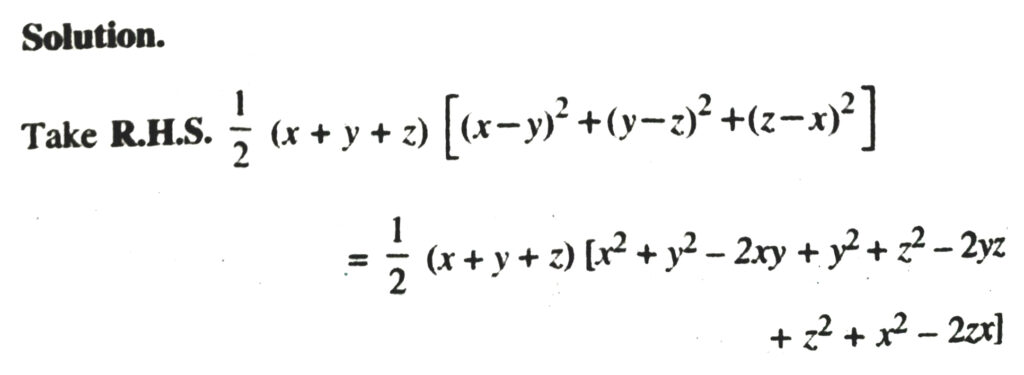
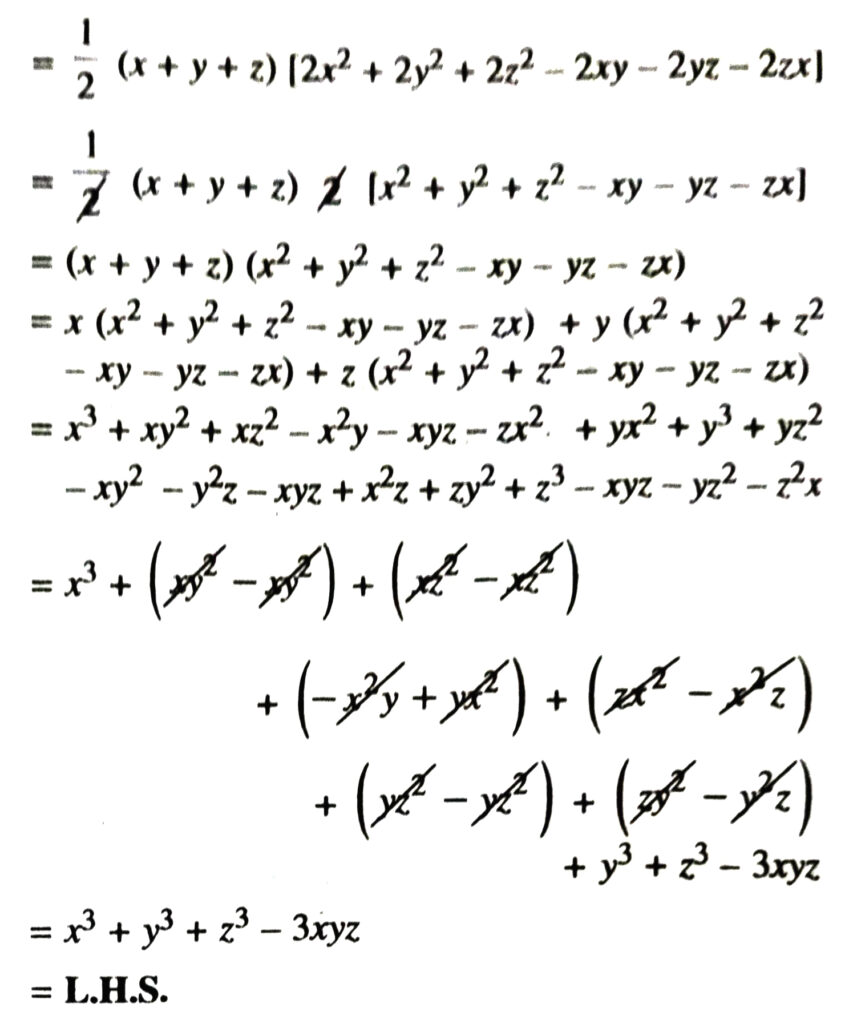
13. If x + y + z = 0,
show that x³ + y³ + z³ = 3xyz
Solution.— x + y + z = 0
⇒ x + y = – z …(i)
Cubing both sides we get :
(x + y)3 = (-z)3
⇒ x³ + y³ + 3xy (x + y) = −z³
⇒ x³ + y³ + 3xy (−z) = −z³ [∴ from (i) x + y = −z]
⇒ x³ + y³ − 3xyz = – z3
⇒ x³ + y³ + z³ = 3xyz Proved.
14. Without actually calculating the cubes, find the value of each of the following :
(i) (−12)³ + (7)³ + (5)³
(ii) (28)³ + (−15)³ + (−13)³.
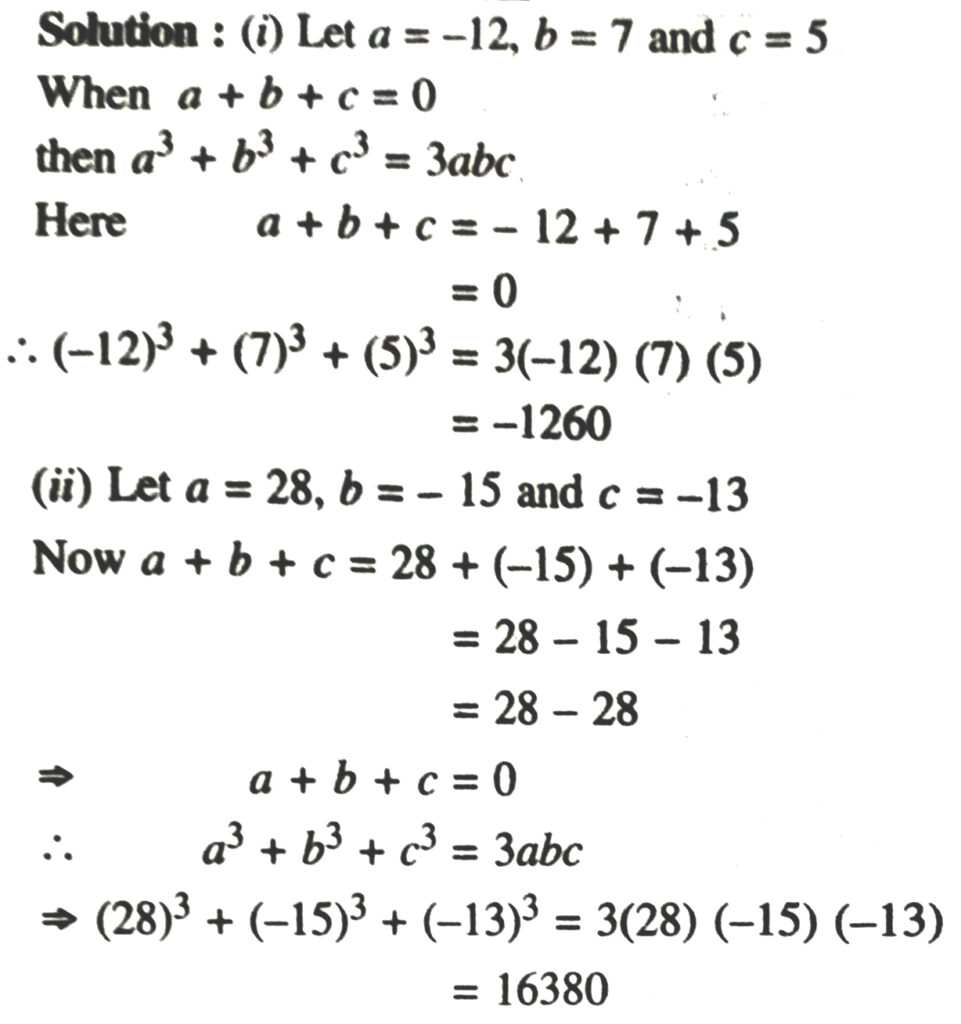
15. Give possible expressions for the length and breadth of the following rectangles, in which their areas are given :

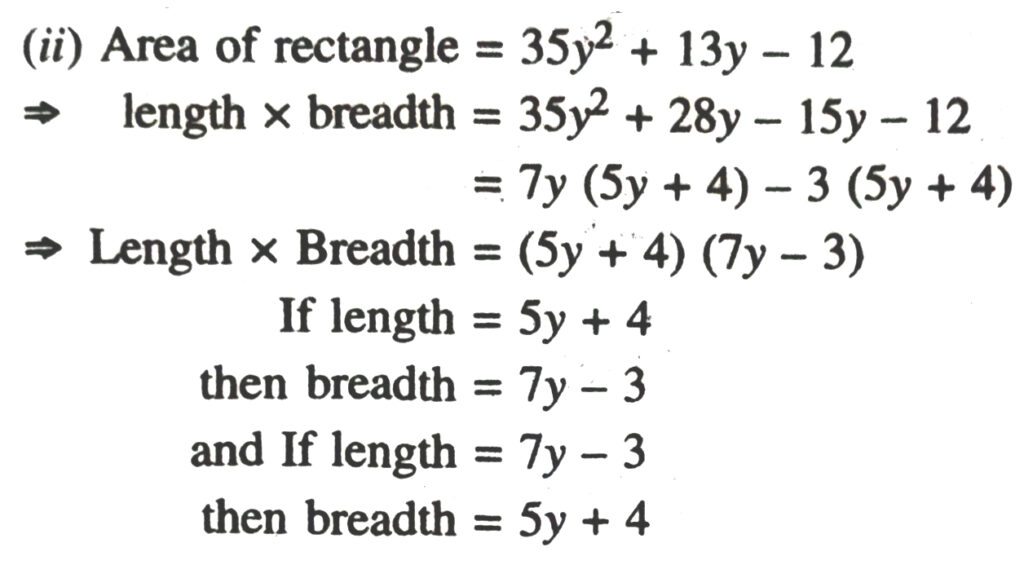
16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below ?
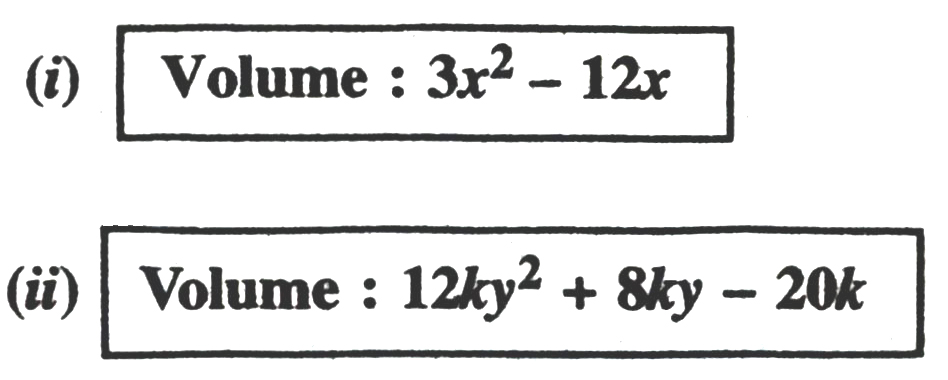

Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here