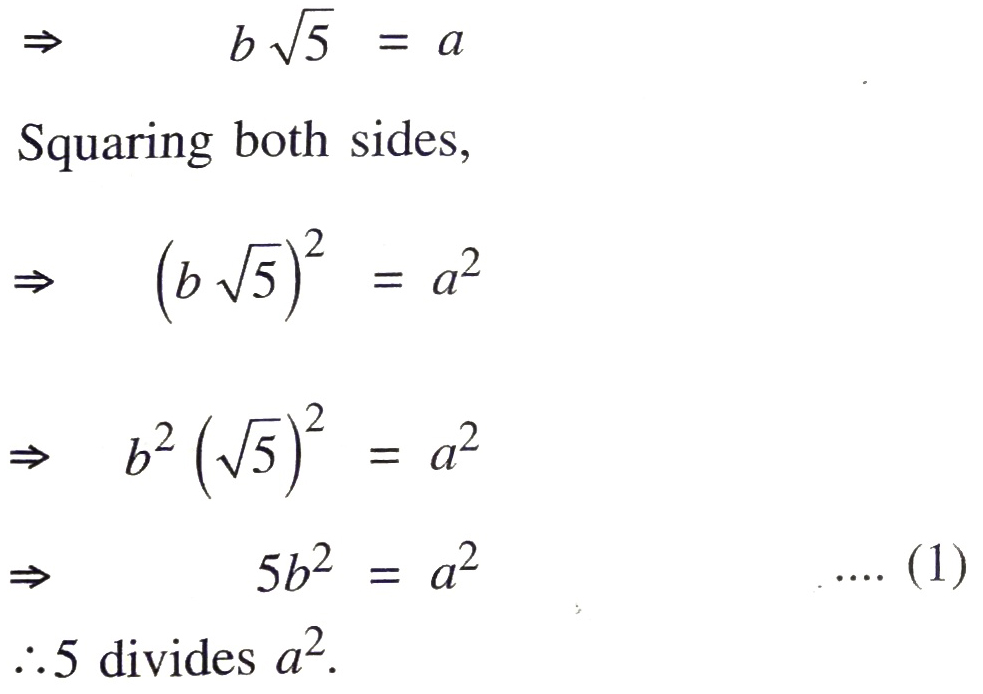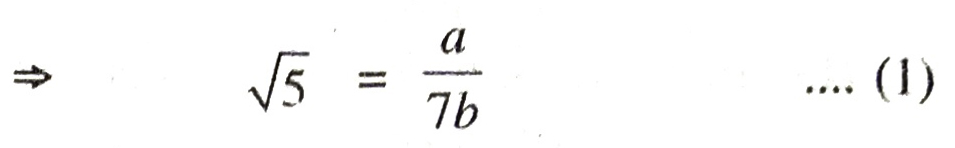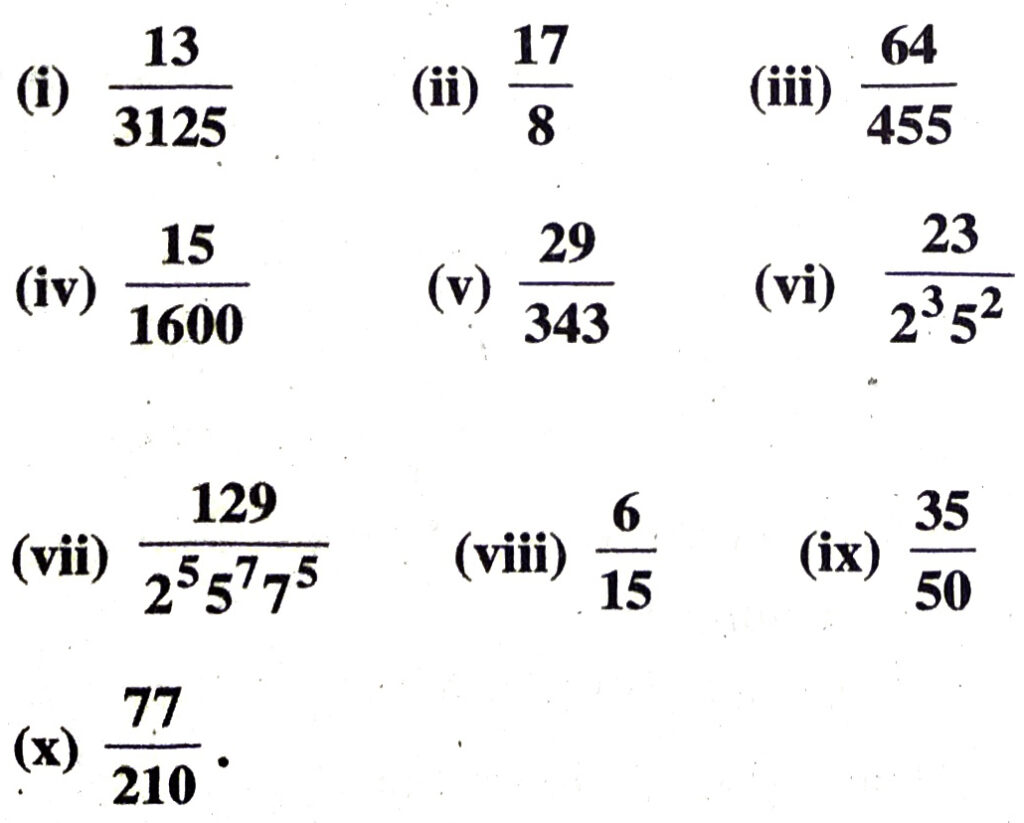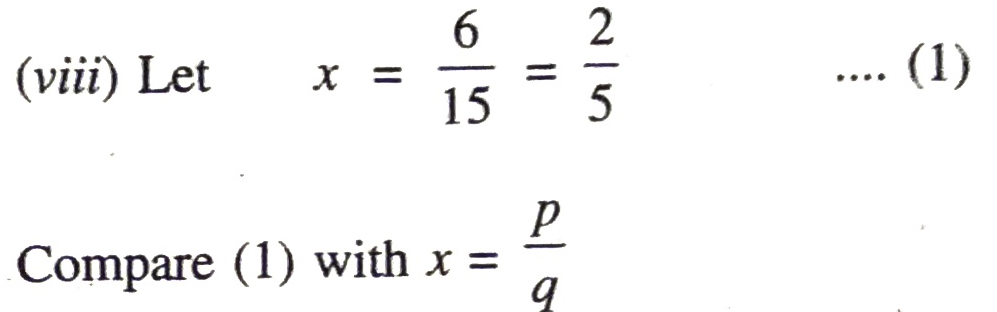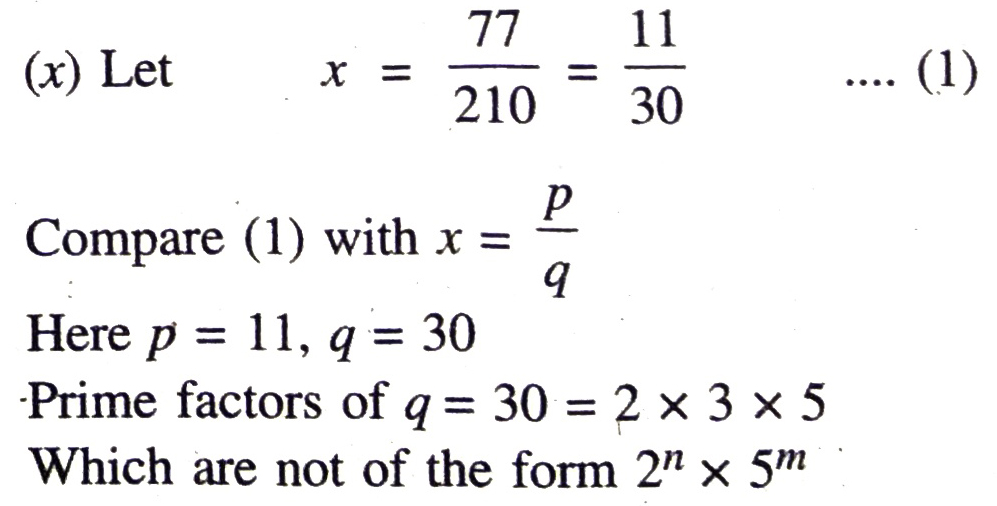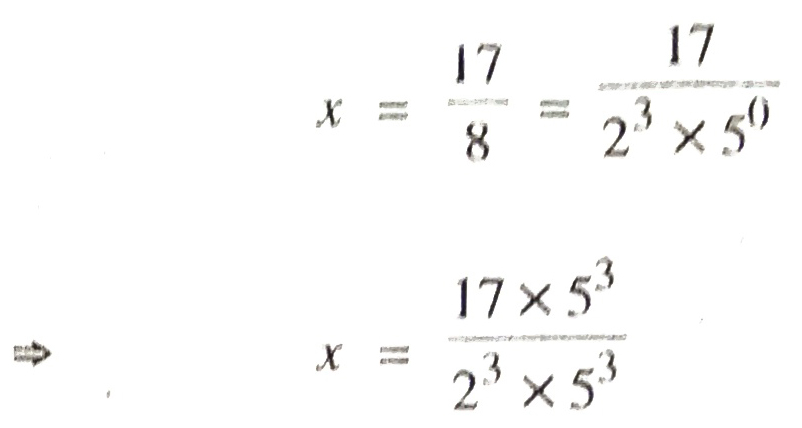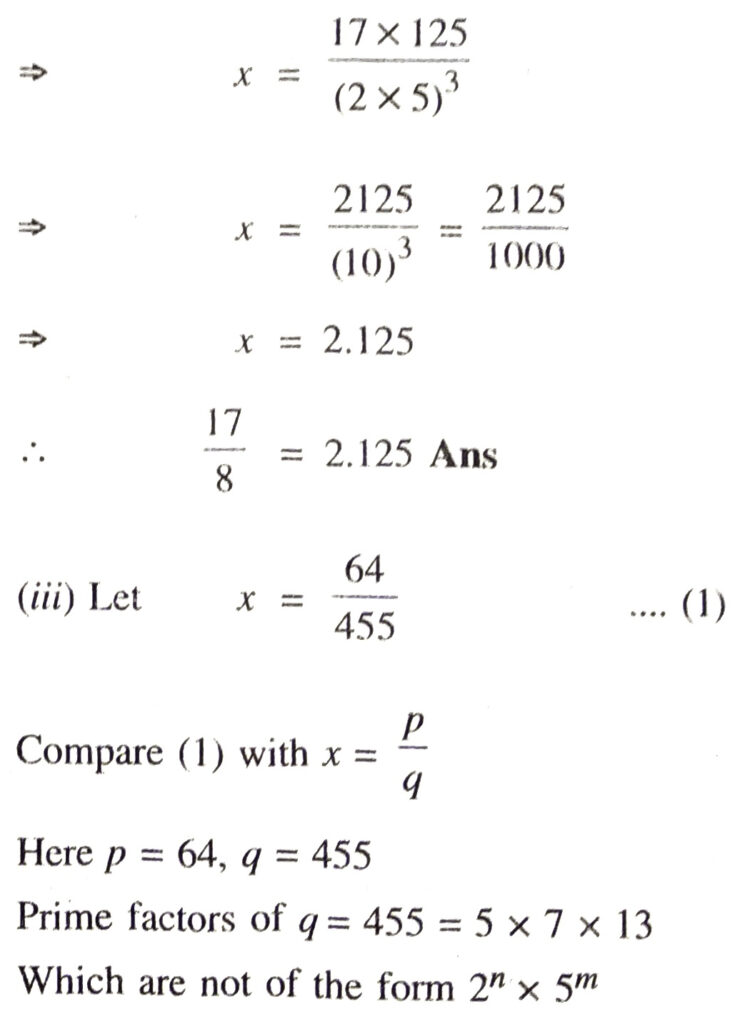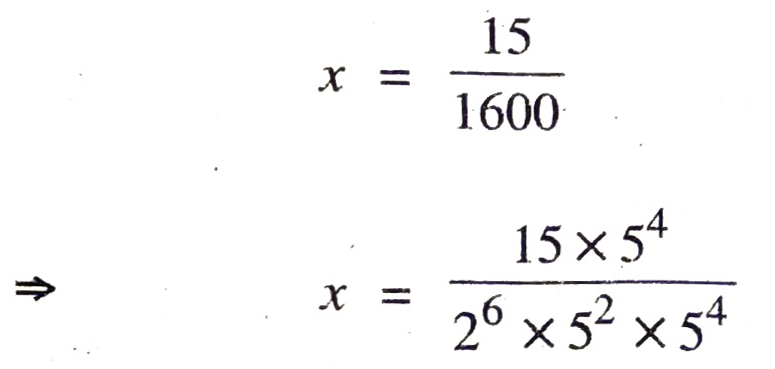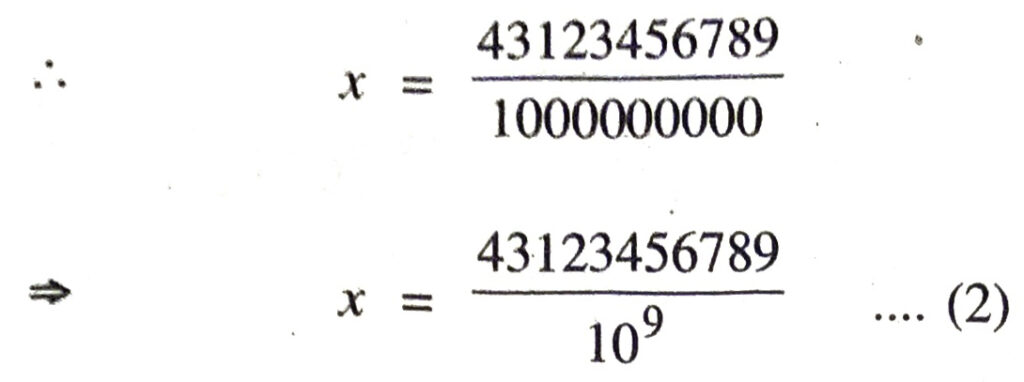JKBOSE 10th Class Maths Solutions chapter – 1 Real Numbers
J&K 10th Class Maths Solutions chapter – 1 Real Numbers
Jammu & Kashmir State Board JKBOSE 10th Class Maths Solutions
INTRODUCTION
Euclid’s division algorithm, as the name suggests, has to do with divisibility of integers. Euclid says any positive integer a can be divided by another positive integer b in such a way that it leaves a remainder r that is smaller than b. Many of us probably recognise that as the usual long division process. Although this result is quite easy to state and understand, it has many applications related to the divisibility properties of integers.
The Fundamental Theorem of Arithmetic, has to do with multiplication of positive integers. Every composite number can be expressed as a product of primes in a unique way-this important fact is the fundamental theorem of arithmetic.
Fundamental Theorem of Arithmetic has two main applications. Firstly, we use it to prove the irrationality of many of the numbers such as √2, √3 and √5 etc. Secondly, we apply this theorem to explore when exactly the decimal expansion of a rational number, say p/q (q≠0), is terminating and when it is non-terminating repeating. We do it by the prime factorisation of q will completely reveal the nature of the decimal expansion of p/q.
TEXT BOOK EXERCISE 1.1
Q. 1. Use Euclid’s division algorithm to find the H.C.F. of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255
Solution. (i) By division Algorithm
Step 1. Since 225 > 135, we apply the division Lemma to 225 and 135, we get
225 = 135 × 1 + 90
Step 2. Since the remainder 90 ≠ 0, we apply the division Lemma to 135 and 90, we get
135 = 90 × 1 + 45
Step 3. Since the remainder 45 ≠ 0, we apply the division Lemma to 90 and 45, we get
90 = 45 × 2 + 0
Since the remainder has now become zero, so we stop procedure
∵ divisor in the step 3 is 45
∴ H.C.F. of 90 and 45 is 45
Hence, H.C.F. of 135 and 225 is 45 Ans.
(ii) H.C.F. of 196 and 38220 is :-
Step 1. Since 38220 > 196, we apply the division Lemma to 196 and 38220, we get
38220 = 196 × 195 + 0
Since the remainder has now become zero so we stop the procedure
∵ divisor in the step 3 is 196
∴ H.C.F. of 38220 and 196 is 196.
Hence, H.C.F. of 38220 and 196 is 196 Ans.
(iii) H.C.F. of 867 and 255 is :-
Step 1. Since 867 > 255, we apply the division Lemma to 867 and 255, we get
867 = 255 × 3 + 102
Step 2. Since remainder 102 ≠ 0, we apply the division Lemma to 255 and 102, we get
255 = 102 × 2 + 51
Step 3. Since remainder 51 ≠ 0, we apply the division Lemma to 51 and 102, by taking 102 as division, we get
102 = 51 × 2 + 0
Since the remainder has now become zero, so we stop the procedure.
∵ divisor in step 3 is 51
∴ H.C.F. of 102 and 51 is 51.
Hence, H.C.F. of 867 and 255 is 51 Ans.
Q. 2. Show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
Solution. Let a be any positive odd integer, we apply the division algorithm with a and b = 6.
Since 0 ≤ r < 6, the possible remainders are 0, 1, 2, 3, 4 and 5.
or a can be 6q or 6q+1, or 6q+ 2, or 6q + 3, or 6q+4, or 6q + 5 where q is quotient, since a is odd
∴ a cannot be equal to 6q, 6q+2, 6q + 4 But all these are divisible by 2
Therefore, any odd integer is of the form 6q+1 or 6q + 3 or 6q + 5.
Q. 3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of column in which they can march ?
Solution. Total number of members in army = 616 and 32
(A band of two groups)
Since two groups are to march in same number of columns and we are to find out the maximum number of columns.
∴ Maximum number of columns H.C.F. of 616 and 32
Step 1. Since 616> 32, we apply the division Lemma to 616 and 32, to get
616 = 32 × 19 + 8
Step 2. Since the remainder 8 ≠ 0, we apply the division Lemma to 32 and 8, to get
32 = 8 × 4 + 0
Since the remainder has now become zero
∵ divisor in the step is 8
∴ H.C.F. of 616 and 32 is 8
Hence, maximum number of columns in which they can march is 8 Ans.
Q. 4. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution. Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2.
If x = 3q
Squaring both sides,
(x)² = (3q)² =9q² = 3 (3q²)
= 3m
where m = 3q² and is an integer
∴ x² = 3m …….. (1)
Now, if x = 3q + 1
Squaring both sides,
x² = (3q + 1)²
x² = 9q² + 1 + 2 × 3q × 1
x² = 3 (3q² + 2q) + 1
x² = 3m + 1 …. (2)
where m = 3q² + 2q where m is also an integer
From (1) and (2),
x² = 3m, 3m + 1
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Q. 5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution. Let x be any positive integer and b=3
x = 3q + r where q is quotient and r is remainder
0 ≤ r < 3
If r = 0 then x = 3q
If r = 1 then x = 3q + 1
If r = 2 then x = 3q + 2
x is of the form 3q or 3q + 1 or 3q + 2
If x = 3q
Cubing both sides,
x3 = (3q)³
x3 = 27q3 = 9 (3q³) = 9m
where m = 3q³ and is an integer
x3 = 9m …….(1)
If x = 3q + 1 cubing both sides,
x³ = (3q + 1)³
x³ = 27q³ + 27q² +9q + 1
= 9 (3q³ + 3q² + q) + 1
= 9m + 1 where
m = 3q³ + 3q² + q and is an integer.
Again x³ = 9m + 1 …..(2)
If x = 3q + 2
Cubing both sides,
(x)³ = (3q + 2)²
= 27q³ + 54q² + 36q +8
x³ = 9 (3q³ + 6q³ + 4q) + 8
x³ = 9m + 8 ……..(3)
wherem = 3q³ + 6q² + 4q
Again x³ = 9m + 8
From (1), (2) and (3) we find that x³ can be of the form 9m, 9m + 1, 9m + 8
Hence, x³ of any positive integer can be of the form 9m or 9m + 1 or 9m + 8.
TEXT BOOK EXERCISE 1.2
Q. 1. Express each number as a product of its prime factors :
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429.
Solution.
(i) Prime factorisation of 140
= (2)² (35) = (2)² (5) (7)
(ii) Prime factorisation of 156
= (2)² (39) = (2)² (3) (13)
(iii) Prime factorisation of 3825
= (3)² (425)
= (3)² (5) (85)
= (3)² (5)² (17)
(iv) Prime factorisation of 5005
= (5) (1001)
= (5) (7) (143)
= (5) (7) (11) (13)
(v) Prime factorisation of 7429
= (17) (437)
= (17) (19) (23)
Q. 2. find the L.C.M. and H.C.F. of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54.
solution. given numbers are 26 and 91
(i) prime factorisation of 26 and 91 are
26 = (2) (13)
and 91 = (7) (13)
H.C.F. (26, 91) = product of least powers of common factors
∴ H.C.F. (26, 9) = 13
and L.C.M. (26, 91) = product of highest powers of all the factors
= (2) (7) (13) = 182
verification :
L.C.M. (26, 91) × H.C.F. (26, 91)
= (13) × (182)
= (13) × (2) × (91)
= (26) × (91)
= product of given numbers.
(ii) given numbers are 510 and 92
prime factorisation of 510 and 92 are
510 = (2) (255) = (2) (3) (85)
= (2) (3) (5) (17)
and 92 = (2) (46) = (2)² (23)
H.C.F. (510, 92) = product of least powers of common factors = 2
L.C.M. (510, 92) = product of highest powers of all the factors
= (2)² (3) (5) (17) (23)
= 23460
verification :
L.C.M. (510, 92) × H.C.F. (510, 92)
= (2) (23460)
= (2) × (2)² (3) (5) (17) (23)
= (2) (3) (5) (17) × (2)² (23)
= 510 × 92
= Product of given numbers.
(iii) Given numbers are 336 and 54
Prime factorisation of 336 and 54 are
336 = (2) (168) = (2) (2) (84)
= (2) (2) (2) (42)
= (2) (2) (2) (2) (21)
= (2)4 (3) (7)
and 54 = (2) (27) = (2) (3) (9)
= (2) (3) (3) (3) = (2) (3)³
H.C.F. (336, 54) = Product of least powers of common factors
= (2) (3) = (6)
L.C.M. (336, 54)= Product of highest powers of all the factors
= (2)4 (3)³ (7)
= 3024
Verification :
L.C.M. (336, 54) × H.C.F. (336, 54)
= 6 × 3024
= (2) (3) × (2)4 (3)³ (7)
= (2)4 (3) (7) × (2) (3)³
= 336 × 54
= Product of given numbers.
Q. 3. Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution.
(i) Given numbers are 12, 15 and 21
Prime factorisation of 12, 15 and 21 are
12 = (2) (6) = (2) (2) (3)
= (2)² (3)
15 = (3) (5)
21 = (3) (7)
H.C.F. (12, 15 and 21) = 3 Ans.
L.C.M. (12, 15 and 21) = (2)² (3) (5) (7) = 420 Ans.
(ii) Given numbers are 17, 23 and 29
Prime factorisation of 17, 23 and 29 are
17 = (17) (1)
23 = (23) (1)
29 = (29) (1)
H.C.F. (17, 23 and 29) = 1 Ans.
L.C.M. (17, 23 and 29) = 17 × 23 × 29 = 11339 Ans.
(iii) Given numbers are 8, 9 and 25
Prime factorisation of 8, 9 and 25 are
8 = (2) (4) = (2) (2) (2) = (2)³ (1)
9 = (3) (3) = (3)² (1)
25 = (5) (5) = (5)² (1)
H.C.F. (8, 9 and 25) = 1 Ans.
L.C.M. (8, 9 and 25) = (2)³ (3)² (5)² = 1800 Ans.
Q. 4. Given that H.C.F. (306, 657) = 9, find L.C.M. (306, 657).
Solution. Given numbers are 306 and 657 H.C.F. (306, 657) = 9
∵ H.C.F. x L.C.M. = Product of given numbers
∴ 9 × L.C.M. (306, 657) = 306 × 657
or L.C.M. (306, 657) =

= 34 × 657
= 22338 Ans.
Q. 5. Check whether 6″ can end with the digit 0 for any natural number n.
Solution. Let us suppose that 6″ ends with the digit 0 for some n ∈ N.
∴ 6n is divisible by 5.
But, prime factor of 6 are 2 and 3
∴ Prime factor of (6)n are (2 x 3)n
⇒ it is clear that in prime factorisation of 6n there is no place for 5.
∵ By Fundamental Theorem of Arithmetic, every composite number can be expressed as a product of primes and this factorisation is unique, apart from the order in which the prime factors occur.
∴ Our supposition is wrong.
Hence, there exists no any natural number n for which 6n ends with the digit zero.
Q. 6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 +5 are composite numbers.
Solution.
Consider, 7 × 11 × 13 + 13 = 13 [7 × 11 + 1] which is not a prime number because it has a factor 13. So, it is a composite number.
Also, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = 5 [7 × 6 × 4 × 3 × 2 × 1 + 1], which is not a prime number because it has a factor 5. So it is a composite number.
Q. 7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point ?
Solution. Time taken by Sonia to drive one round of the field = 18 minutes
Time taken by Ravi to drive one round of same field = 12 minutes
They meet again at the starting point = L.C.M. (18, 12)
Now, Prime factorisation of 18 and 12 are
18 = (2) (9) = (2) (3) (3) = (2) (3)²
12 = (2) (6) = (2) (2) (3) = (2)² (3)
L.C.M. (18, 12)= (2)² (3)² = 4 × 9 = 36
Hence, after 36 minutes Sonia and Ravi will meet again at the starting point. Ans.
TEXT BOOK EXERCISE 1.3
Q. 1. Prove that √5 is irrational.
Solution. Let us suppose that √5 is rational so we can find integers r and s where s ≠ 0
such that √5 = r/s
Supposer and s have some common factor other than 1, then divide r and s by the common factor to get :
√5 = a/b where a and b are coprime and b ≠ 0
By the theorem, if a prime number ‘p’ divides a2 then ‘p’ divides a where a is positive integer
⇒ 5 divides a ……. (2)
So a 5c for some integer c.
Put the value of a in (1),
5b² = (5c)²
56² = 25c²
b² = 5c²
or 5c² = b²
⇒ 5 divides b²
∵ if a prime number ‘p‘ divides a², then p divides a ; where a is positive integer.
⇒ 5 divides b. ………(3)
From (2) and (3), a and b have at least 5 as common factor.
But this contradicts the fact that a and b are coprime i.e. no common factor other than 1.
∴ our supposition that √5 is rational is wrong.
Hence √5 is irrational.
Q. 2. Prove that 3+2√5 is irrational.
Solution. Let us suppose that 3+2√5 is rational.
∴ we can find Co-Prime a and b, where a and b are integers and b ≠ 0
∴ our supposition is wrong.
Hence 3+2√5 is rational.
Q. 3. Prove that the following are irrationals:
∴ we can find co-prime integers a, b and b ≠ 0
because division of two integers is a rational number
So 2a/b = rational number
∴ from (1), √2 is also a rational number,
which contradicts the fact that √2 is irrational.
∴ our supposition is wrong.
Let us suppose that 7√5 is rational
∴ we can find coprime integers a and b where b ≠ 0
Since a, 7 and b all are integers and division of two integers is a rational number.
which contradicts the fact that √5 is irrational.
∴ our supposition is wrong.
Hence 7√5 is irrational.
(iii) Given that 6+√2
Let us suppose that 6+√2 is rational
∴ we can find coprime integers a and b where b ≠ 0
which contradicts the fact that √2 is irrational number.
∴ Our supposition is wrong.
Hence 6+√2 is irrational.
TEXT BOOK EXERCISE 1.4
Q. 1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion :
Compare (1) with x = p/q
Here P = 15 and q = 1600
Prime factors of q = 600 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 = 26 x 52
which are of the form 2n x 5m, here n = 6, m = 2
and these are non negative integers.
∴ x = 15/1600 having terminating decimal expansion. Ans.
(v) Let x = 29/343 ………(1)
Compare (1) with x = p/q
Here P = 29 and q = 343
Prime factors of q = 343 = 7 x 7 x 7 = 7³
Which are of the form 2n x 5m
∴ x = 29/343 will have a non terminating repeating decimal expansion. Ans
(vi) Let x = 23/2³5² …. (1)
Compare (1) with x = p/q
Here p = 23 and q = 2³5²
Prime factor of q = 2³5² which are of the form 2n x 5m here n 3, m = 2 and these are non negative integers.
∴ x = 23/2³5² have a terminating decimal expansion. Ans.
(vii) Let x = 129/25 57 75 ……..(1)
Compare (1) with x = p/q
Here p = 129 and q = 22 57 75
Prime factors of q = 22 57 75
Which are not of the form 2n x 5m
∴ x = 129/22 57 75 have a non-terminating decimal expansion. Ans
Here p = 2, q = 5
Prime factors of q = 5 = 20 x 51
Which are of the form 2n x 5m here n = 0, m = 1 and these are non negative integers
∴ x = 6/15 have a terminating decimal expansion. Ans.
Here p = 7, q = 10
Prime factors of q = 10 = 2 x 5 = 21 x 51
Which is of the form 2n x 5m here n = 1, m = 1
both n and m are non negative integer.
∴ x = 35/50 have a terminating decimal expansion. Ans.
∴ x = 77/210 have a non-terminating decimal expansion. Ans
Q. 2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solution. (i) Let x = 13/3125 ……..(1)
Compare (1) with x = p/q
Here p = 13. q = 3125
Prime factors of q = 3125 = 5 × 5 × 5 × 5 × 5 = 55 × 20
Which are of the form 2n x 5m, where n = 0, m = 5 and these are non negative integers
∴ x = 13/3125 have a terminating decimal expansion.
To Express in Decimal form
[ we are to make 10 in the denominator so multiply and divide by 25]
Prime factors of q = 8 = 2 x 2 x 2 = 2³ × 50 Which are of the form 2n x 5m, where n = 3, m = 0
and these are non negative integers.
∴ x = 17/8 can be expressed as a terminating decimal expansion.
To Express in Decimal form
[Multiply & divide with 53 to make the denominator 10]
∴ x = 64/455 has a non-terminating repeating decimal expansion. Ans.
(iv) Let x = 15/1600 …….(1)
Compare (1) with x = p/q
Here P = 15, q = 1600
Prime factors of q = 1600 = 2×2×2×2×2×2×5×5 = 26 x 52
Which is of the form 2n x 5m, here n = 6, m = 2 and these are non negative integers.
∴ x = 15/1600 having terminating decimal expansion.
To Express in Decimal form
[To make denominator a power of 10 multiply and divide by 54]
Here p = 29 and q = 343 = 7x7x7=7³ Which are not of the form 2n x 5m
∴ x = 29/343 will have a non terminating repeating decimal expansion.
To Express in Decimal form
To Express in Decimal form

Which are of the from 2n x 5m hare n = 1, m = 1
and both n and m are non-negative integer
∴ x = 7/10 have a terminating decimal expansion.
To Express in Decimal form
∴ x = 77/210 have a non-terminating decimal expansion. Ans.
Q. 3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p/q, what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000……
(iii) 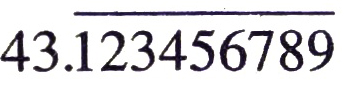
Solution. (i) Let x = 43.123456789 ……..(1)
It is claer from the number that x is rational number.
Now remove the decimal from the number
From (2) x is a rational number and of the form p/q.
Where p = 43123456789 and q = 10⁹
Now. Prime factors of q = 10⁹ = (2 × 5)⁹
⇒ Prime factors of q are 29 x 59 Ans.
(ii) Let x = 0.120120012000120000……
It is clear from the number that it is an irrational number.
(iii) Let x =
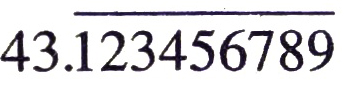
……….(1)
It is clear that the given number is a rational number because it is non terminating and repeating decimal.
To show that (i) is of the form p/q
Multiply (1) with 109 on both sides,
10⁹ x = 43123456789.123456789… …….(2)
Subtract (1) from second, we get :
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here