JKBOSE 10th Class Maths Solutions chapter – 2 Polynomials
JKBOSE 10th Class Maths Solutions chapter – 2 Polynomials
J&K 10th Class Maths Solutions chapter – 2 Polynomials
Jammu & Kashmir State Board JKBOSE 10th Class Maths Solutions
INTRODUCTION
An algebraic expression is a combination of terms connected by the operations of addition, subtraction, multiplication and division.
Polynomial
An algebraic expression of the form
p (x) = a0xn + a1xn-1 + a2xn-2 + ……… + an-1x + an
where ao, a0, a1, a2, ……….. an are real numbers provided a0 ≠ 0; n is non-negative integer is called a polynomial in x.
In simple words, an algebraic expression with more than one term is called a polynomial, provided it has no negative exponent for any variable in the terms.
Degree of Polynomial.
The highest power of x in p (x) is called the degree of the polynomial p (x).
(1) A polynomial of degree 1 is called a linear polynomial.
(2) A polynomial of degree 2 is called a quadratic polynomial.
(3) A polynomial of degree 3 is called a cubic polynomial.
General form of Polynomial.
(1) ax + b; a ≠ 0 is linear polynomial.
(2) ax² + bx + c; a ≠ 0, a, b, c are real numbers, is a quadratic polynomial.
(3) ax³ + bx² + cx + d; a ≠ 0, a, b, c, d are real numbers, is cubic polynomial.
Value of Polynomial.
If p (x) is a polynomial in x, and if k is any real number, then the real number obtained by replacing x by k in p (x), is called the value of p (x) at x = k and is denoted by p (k).
Zero of Polynomial
A real number k is said to be a zero of a polynomial p (x) if p (k) = 0
In general, p (x) = ax + b
⇒ P (k) = ak + b
⇒ P (k) = 0
⇒ ak + b = 0
⇒ k = -b/a
It is clear that, zero of a linear polynomial is related to its coefficients.
Geometrical meaning of the zeros of a Polynomial.
TEXT BOOK EXERCISE 2.1
Q. 1. The graphs of y = p (x) are given in Fig. below, for some polynomials p(x). Find the number of zeroes of p (x), in each case.
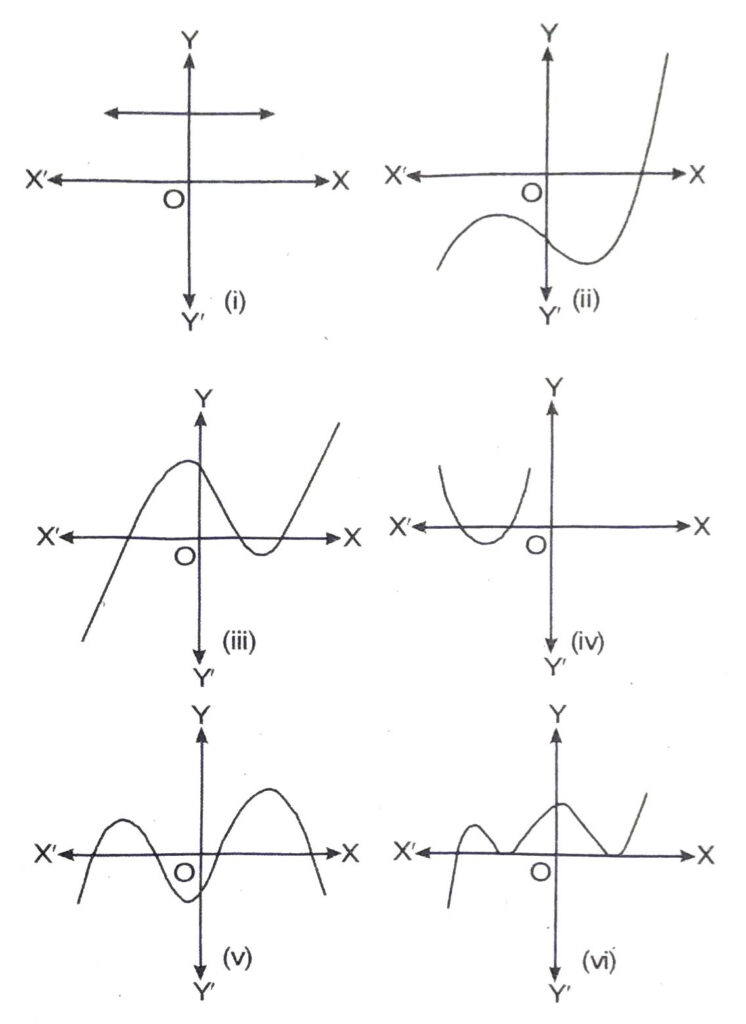
Solution. The graphs of y = p (x) are given in figure below, for some polynomials p (x). The number of zeroes of p (x) in each case are given below :
(i) From the graph, it is clear that it does not meet x-axis at any point.
Therefore, it has NIL; no. of zeroes.
(ii) From the graph, it is clear that it meets x-axis at only one point.
Therefore, it has only one no. of zeroes.
(iii) From the graph, it is clear that it meets x-axis at three points.
Therefore, it has three; no. of zeroes.
(iv) From the graph, it is clear that it meets x-axis at two points.
Therefore, it has two; no. of zeroes.
(v) From the graph, it is clear that it meets x-axis at four points.
Therefore, it has four; no. of zeroes.
(vi) From the graph, it is clear that it meets x-axis at three points.
Therefore, it has three; no. of zeroes.
TEXT BOOK EXERCISE 2.2
Q. 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x − 8
(ii) 4s² − 4s + 1
(iii) 6x²-3-7x
(iv) 4u² + 8u
(v) t²-15
(vi) 3x²-x-4
Solution. (i) Given quadratic polynomial,

Hence, relationship between the zeroes and the coefficient are verified.
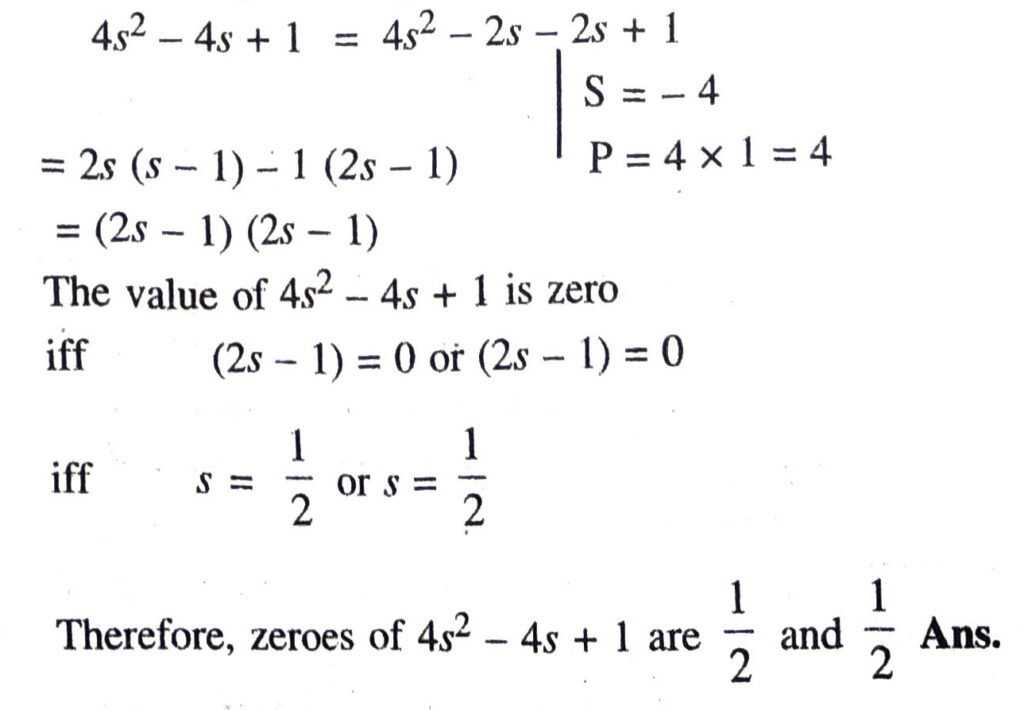

Hence, relationship between the zeroes and the coefficients are verified.
(iii) Given quadratic polynomial,
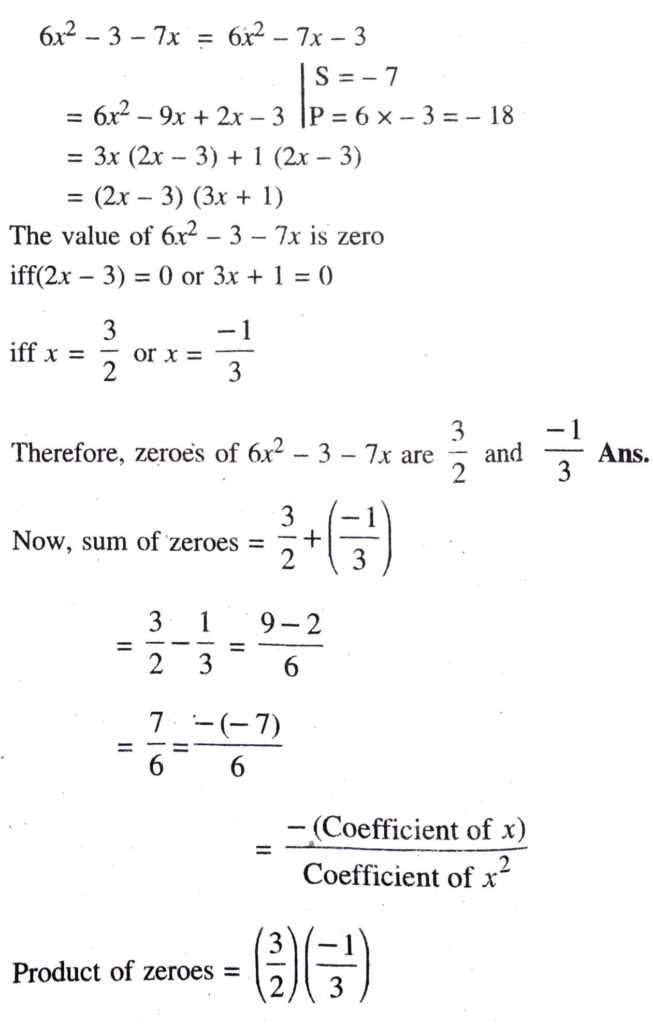

Hence, relationship between the zeroes and the coefficients are verified.
(iv) Given quadratic polynomial,
4u² + 8u = 4u (u + 2)
The value of 4u² + 8u is zero
iff 4u = 0 or u + 2 = 0
iff u = 0 or u = – 2
Therefore, zeroes of 4u² + 8u re 0 and -2 Ans.

Hence, relationship between the zeroes and the coefficients are verified.
(v) Given quadratic polynomial,


Hence, relationship between the zeroes and the coefficients are verified.
(vi) Given quadratic polynomial,

Hence, relationship between the zeroes and the coefficients are verified.
Q. 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
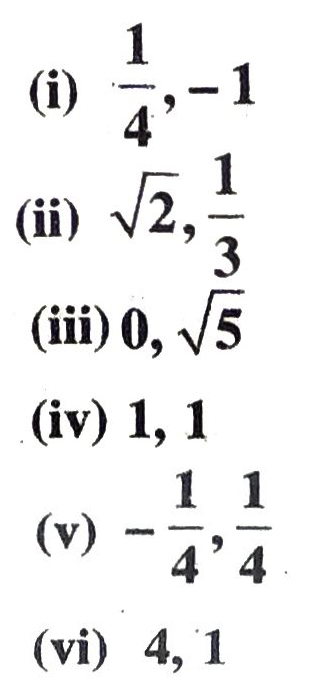
Solution. Given that, sum of zeroes and products of zeroes of given polynomial are 1/4 and -1 respectively.
(i) Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.

for different value of k, we get different quadratic polynomials.
(ii) Given that, sum of zeroes and product of zeroes of given quadratic polynomial are √2 and 1/3 respectively.
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
∴ α + β = Sum of zeroes = √₂
and αβ = Product of zeroes = 1/3
Now, ax² + bx + c = k (x − a) (x − β), where k is any constant
= k [x² − (α +β) x + αβ]
= k [x² = √2x + 1/3]
for different values of k, we get different quadratic polynomial.
(iii) Given that, sum of zeroes and products of zeroes of given quadratic polynomial are 0 and √5 respectively.
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
∴ α + β = Sum of zeroes = 0
and αβ = Product of zeroes = √5
Now, ax² + bx + c = k (x − α) (x − β), where k is any constant
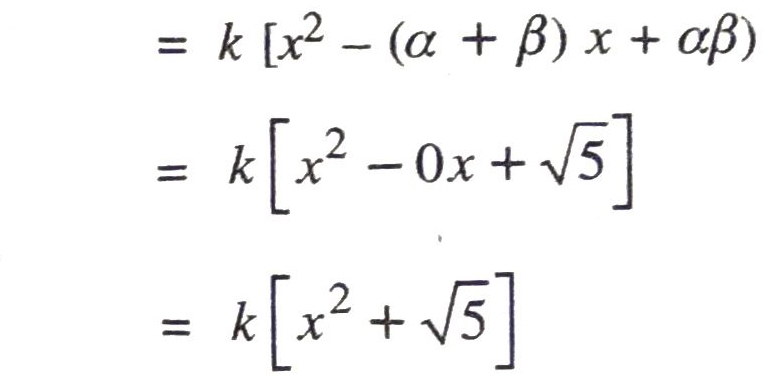
for different values of k, we get different quadratic polynomial.
(iv) Given that, sum of zeroes and product of zeroes of given quadratic polynomial are 1 and 1 respectively.
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
∴ α + β = Sum of zeroes = 1
and αβ = Product of zeroes = 1
Now, ax² + bx + c = k (x − α) (x − β), where k is any constant.
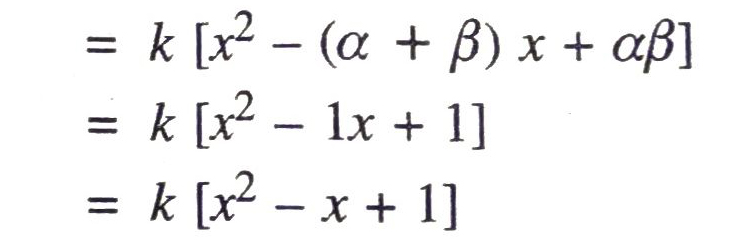
for different values of k, we get different quadratic polynomial.
(v) Given that, sum of zeroes and product of zeroes of given quadratic polynomial are -1/4 and 1/4 respectively.
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
∴ α+β = Sum of zeroes = -1/4
and αβ = Product of zeroes = 1/4
Now, ax2+bx+c = k (x-α) (x-β), where k is any constant
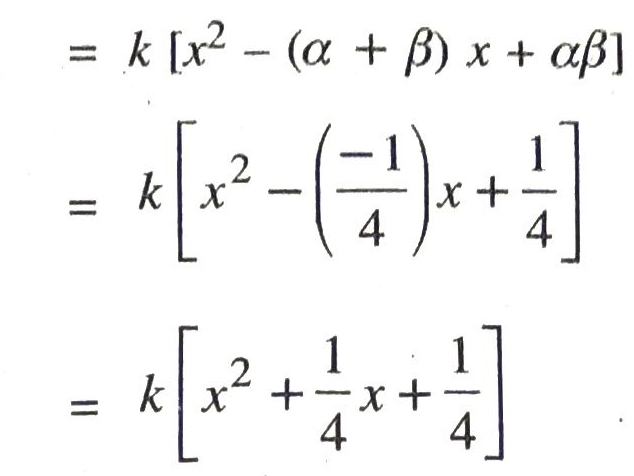
For different values of k, we get different quadratic polynomial.
(vi) Given that, sum of zeroes and product of zeroes of given polynomial are 4 and 1 respectively.
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
∴ α + β = Sum of zeroes = 4
and αβ = Product of zeroes = 1
Now ax² + bx + c = k (x − α)(x − β), where k is any constant
= k [x² – (α +β)x + αβ]
= k [x² – 4x + 1]
for different value of k, we get different quadratic polynomials.
TEXT BOOK EXERCISE 2.3
Q. 1. Apply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below :
(i) p (x) = x³ – 3x² + 5x – 3, g (x) = x² − 2
(ii) p (x) = x4 -3x² + 4x + 5, g (x) = x² + 1 -x
(iii) p (x) = x4 – 5x + 6, g (x) = 2 – x²
Solution. (i) Given that p (x) = x³ − 3x² + 5x – 3 and g (x) = x² -2
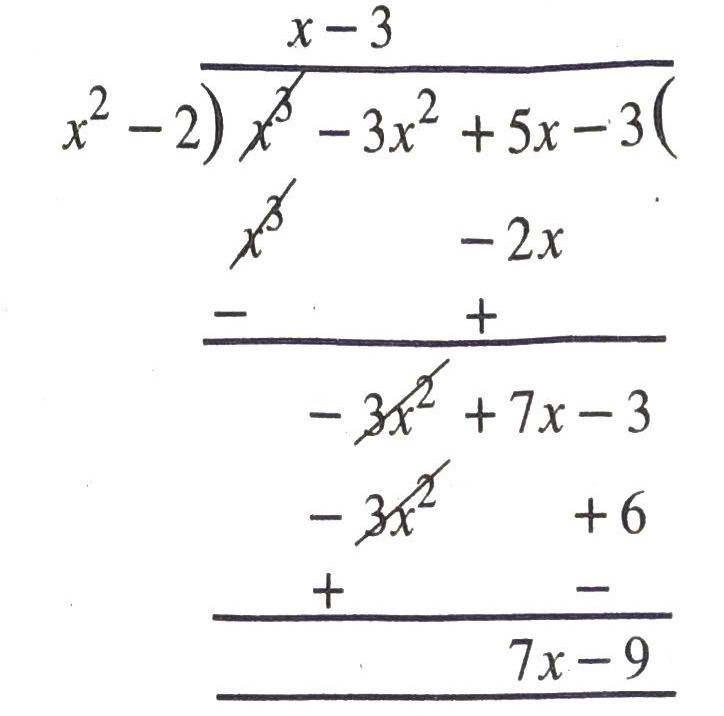
By division algorithm,
x³ -3x² + 5x – 3 = (x − 3) (x² − 2) + (7x −9)
Hence, quotient = x-3 and remainder = 7x – 9 Ans.
(ii) Given that p (x) = x4 – 3x² + 4x + 5
or p (x) = x4 + 0x3 – 3x4 + 4x + 5
and g (x) = x² + 1 – x
or g (x) = x² – x + 1
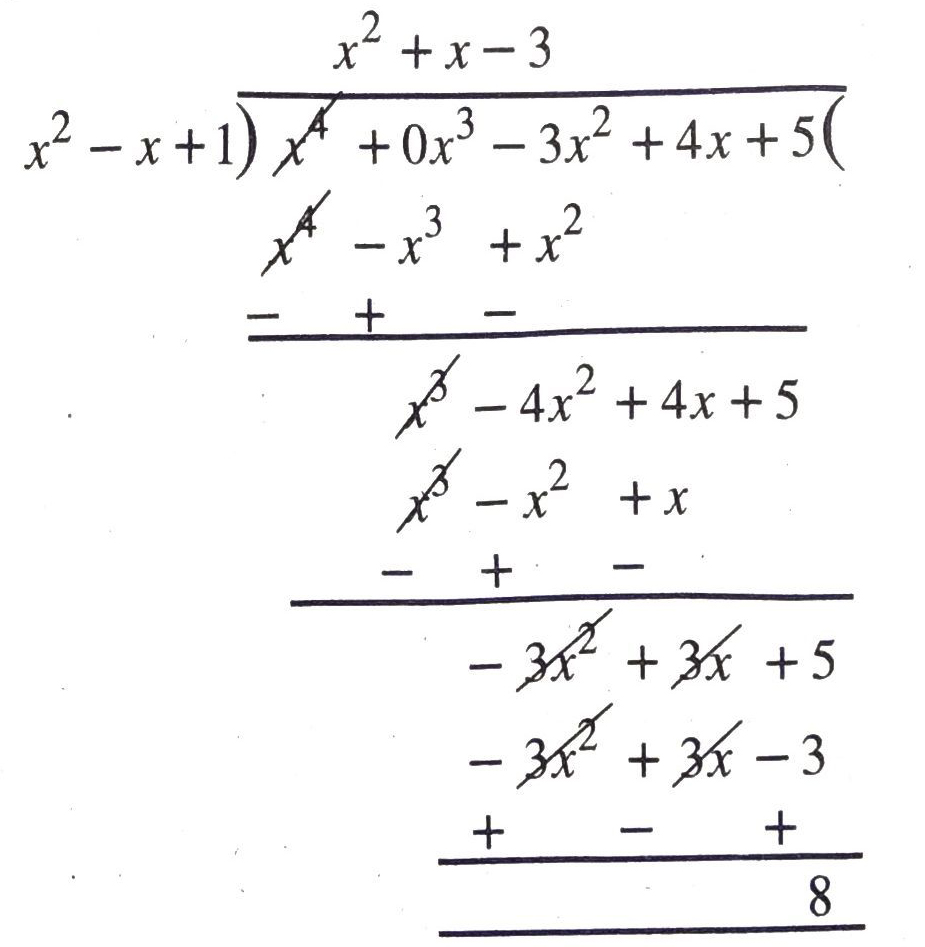
By Division Algorithm,
x4 -3x² + 4x + 5 = (x² + x − 3) (x² − x + 1) + 8
Hence, quotient = x² + x – 3
and remainder = 8 Ans.
(iii) Given that p (x) = x4 – 5x + 6
or p (x) = x4 0x³ + 0x2 – 5x + 6
and g (x) = 2 – x²
or g (x) = – x² + 2
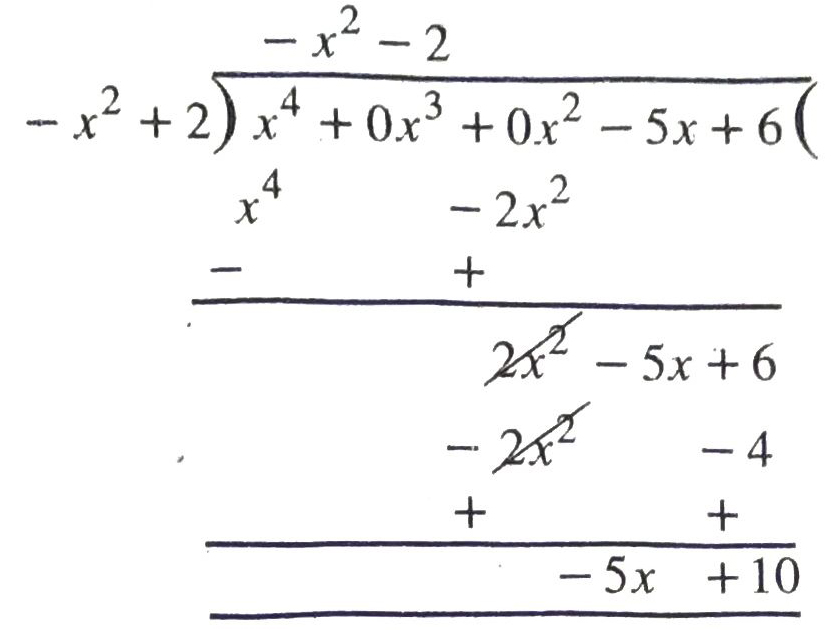
By division algorithm,
x4 – 5x + 6 = (− x² − 2) (− x² + 2) + (− 5x + 10)
Hence, quotient = -x² – 2, remainder = – 5x + 10 Ans.
Q. 2. Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm:
(i) t² – 3, 2t4 + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x4 + 5x³ − 7x² + 2x + 2
(iii) x³ – 3x + 1, x5 – 4x³ + x² + 3x + 1
Solution. (i)
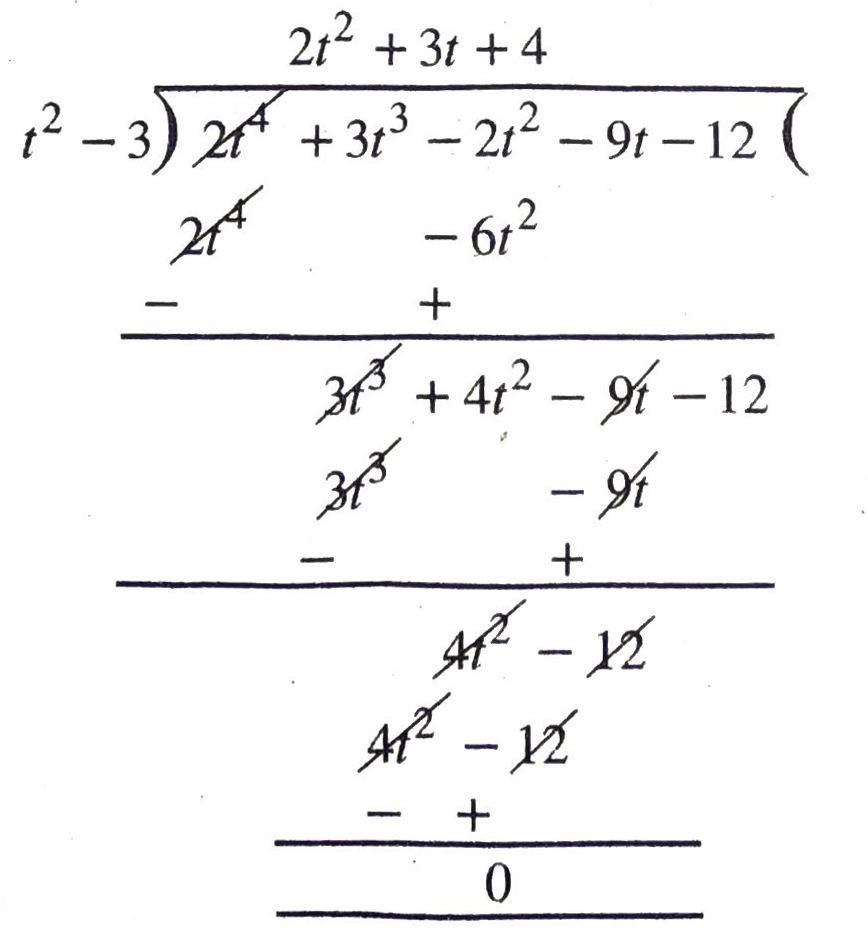
∴ remainder is zero
∴ By division algorithm,
t² – 3 is factor of 2t4 +3t³-2t² – 9t – 12 Ans.
(ii)
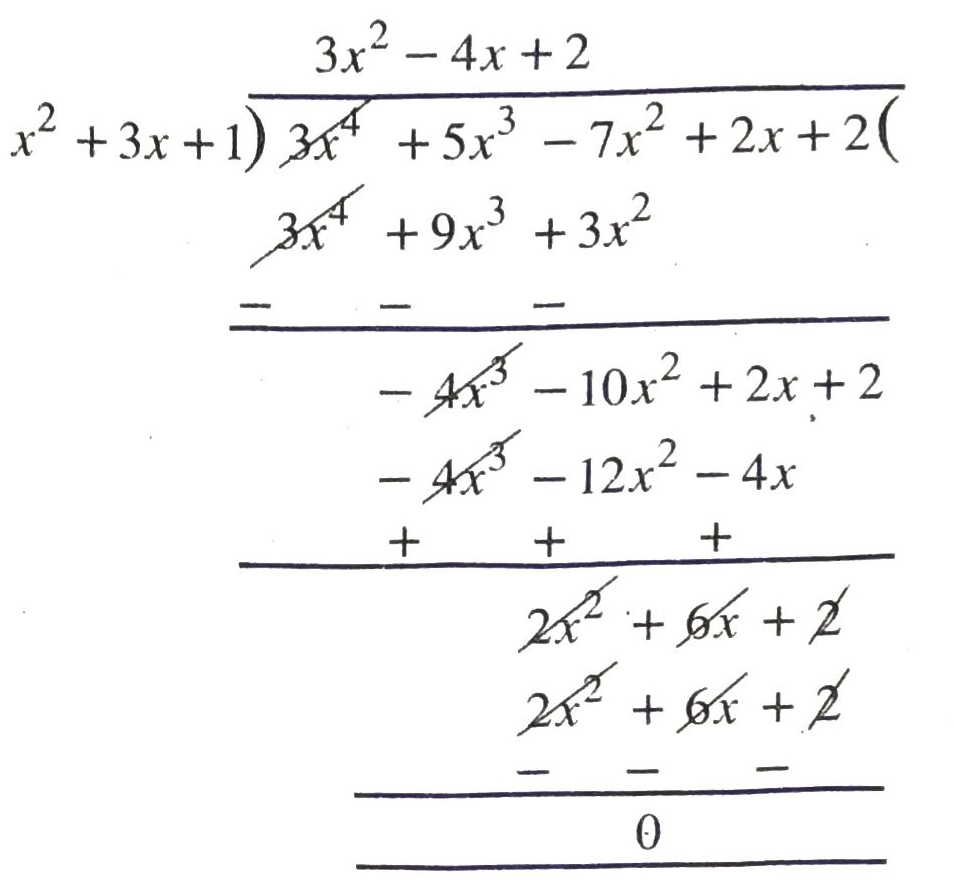
∴ remainder is zero,
∴ By division algorithm,
x² + 3x + 1 is a factor of 3x4 + 5x³ – 7x² + 2x + 2 Ans.
(iii)
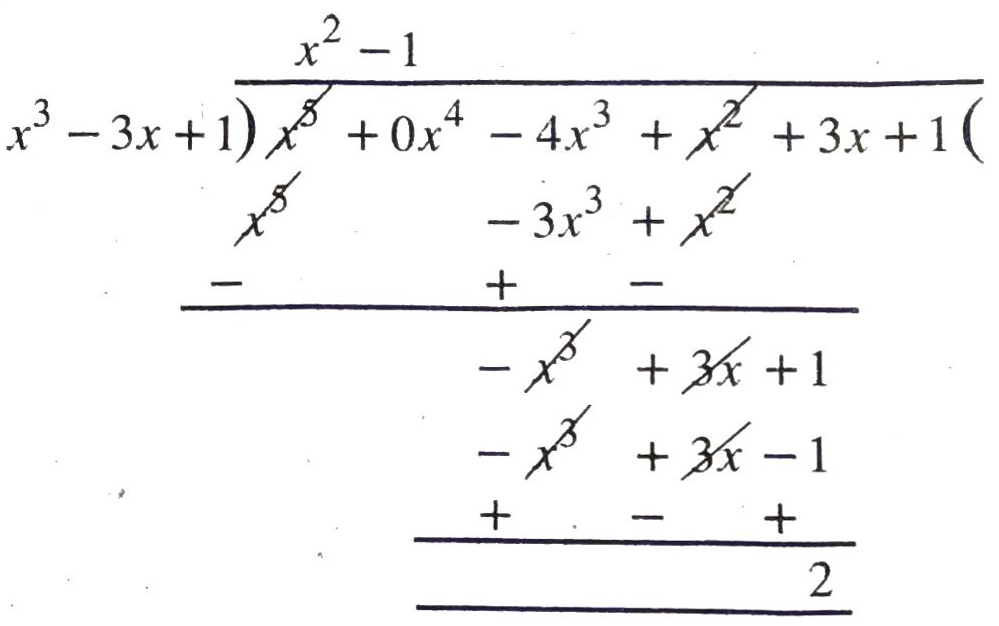
∴ remainder is not zero.
∴ By division algorithm,
x³ – 3x + 1 is not a factor of x5 – 4x³ + x² + 3x + 1 Ans.
Q. 3. Obtain all other zeroes of 3x4 + 6x³ – 2x² – 10x – 5, if two of its zeroes are 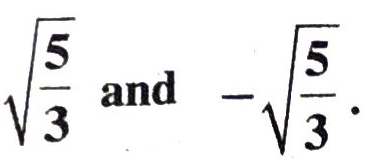
Solution. Given that two zeroes are 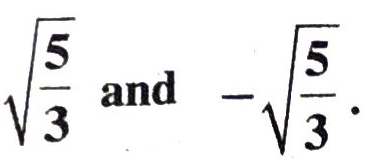


Q. 4. On dividing x³ – 3x² + x + 2 by a polynomial g (x), the quotient and remainder were x – 2 and – 2x + 4 respectively, find g (x).
Solution. Let p (x) = x³ − 3x² + x + 2
and q (x) = (x – 2) and r (x) = – 2x + 4
Compare given data with division algorithm, we have
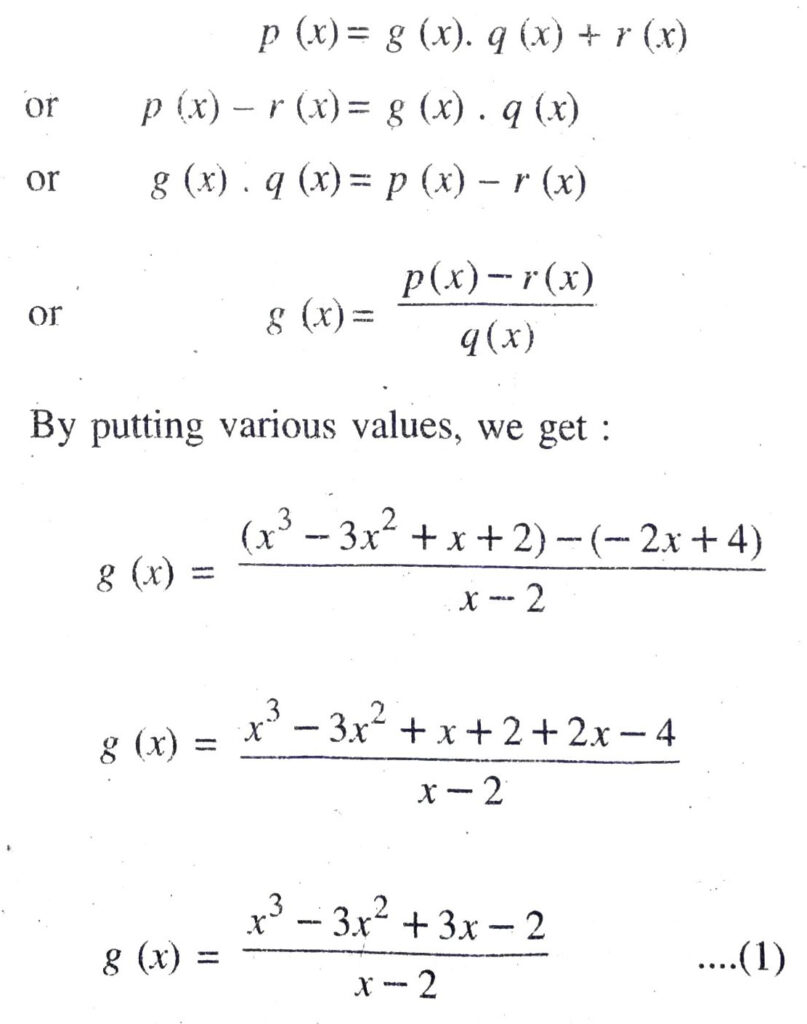
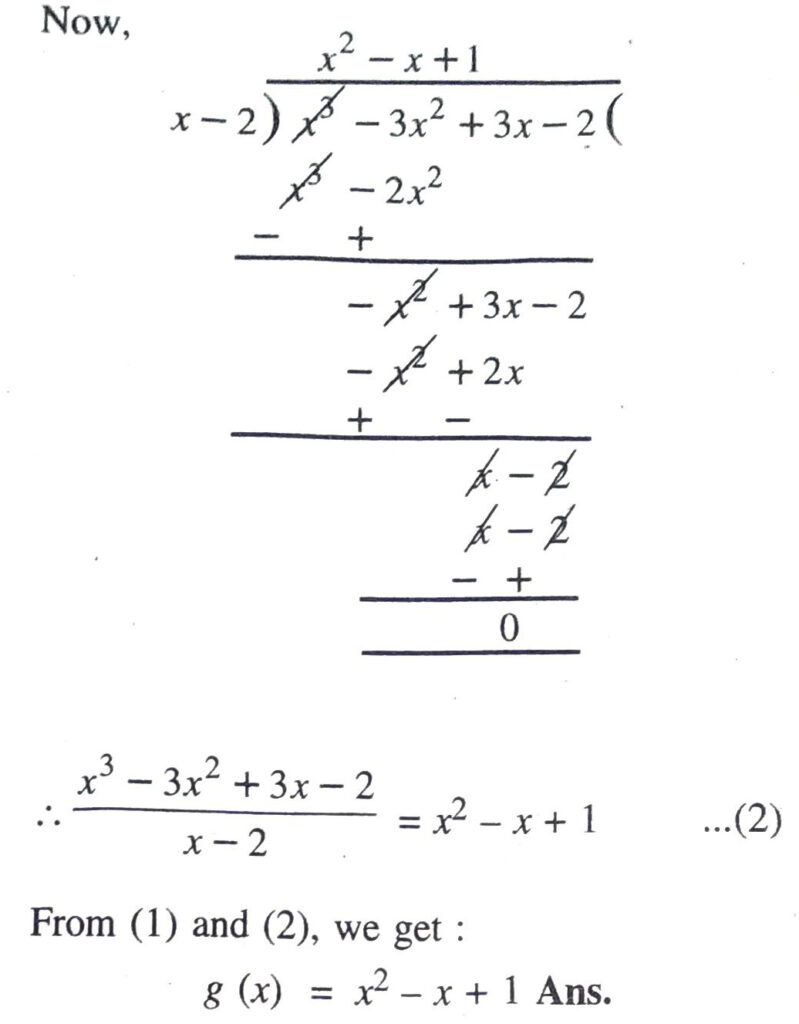
Q. 5. Give examples of polynomials p (x), g (x), q (x) and r (x), which satisfy the division algorithm and
(i) deg p (x) = deg q (x)
(ii) deg q (x) = 0
(iii) deg q (x) = deg r (x)
Solution. (i) Let p (x) = 5x² – 5x + 10; g (x) = 5 q (x) x² – x + 2; r (x) = 0
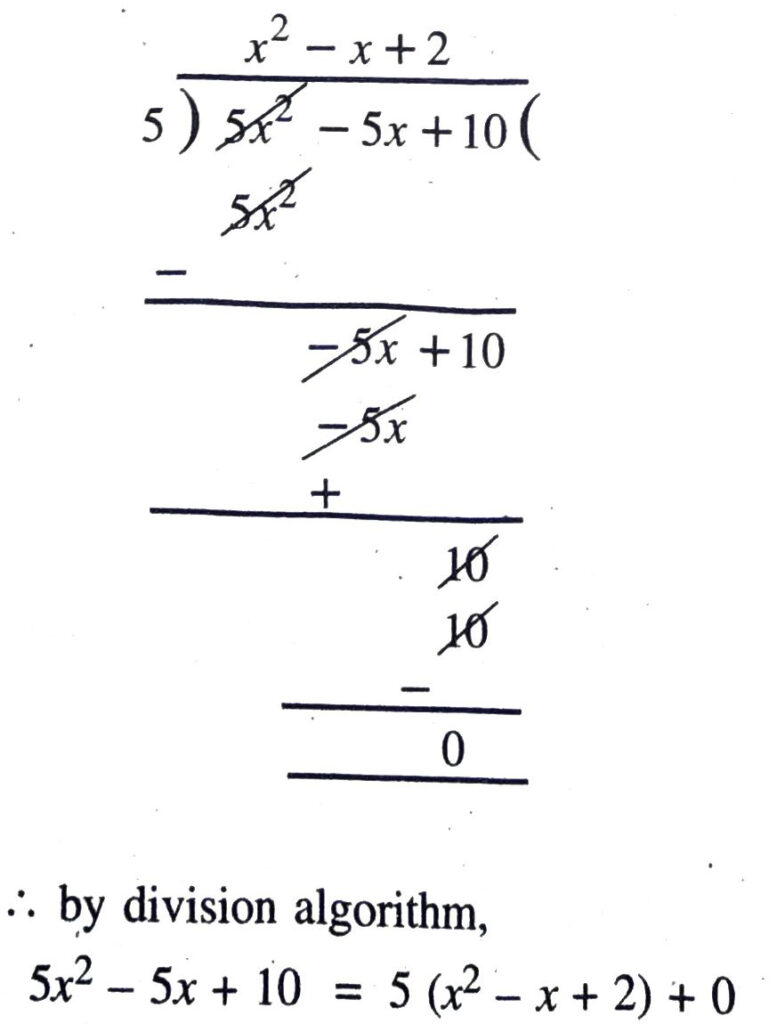
or p (x) = g (x) q (x) + r (x)
Also, deg p (x) = deg q (x) = 2
(ii) Let p (x) = 7x3 – 42x +53;
g (x) = x3 – 6x + 7; q (x) = 7; r (x) = 4

∴ by division algorithm,
4x³ + x² + 3x + 6 = (4x − 11) (x² + 3x + 1) + (32x + 17)
or p (x) = q (x) . g (x) + r (x)
Also, deg q (x) = deg r (x)
TEXT BOOK EXERCISE 2.4
(OPTIONAL)
Q. 1. Verify that the number given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :

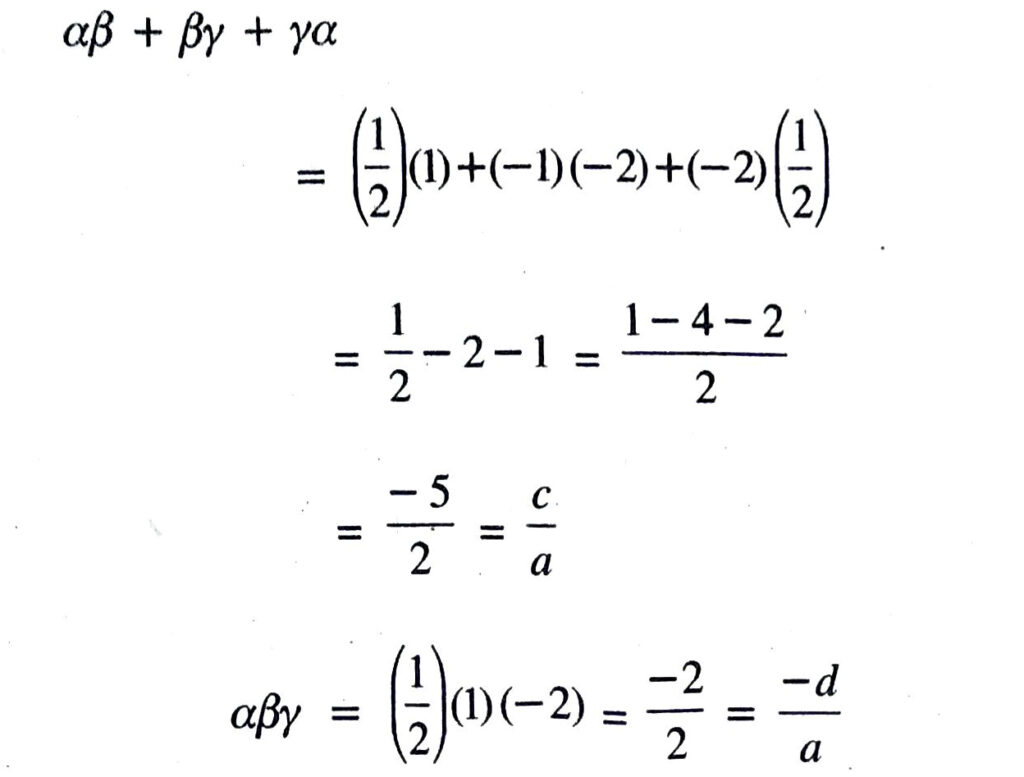
From above discussion, it is clear that is a relationship between zeroes and coefficients.
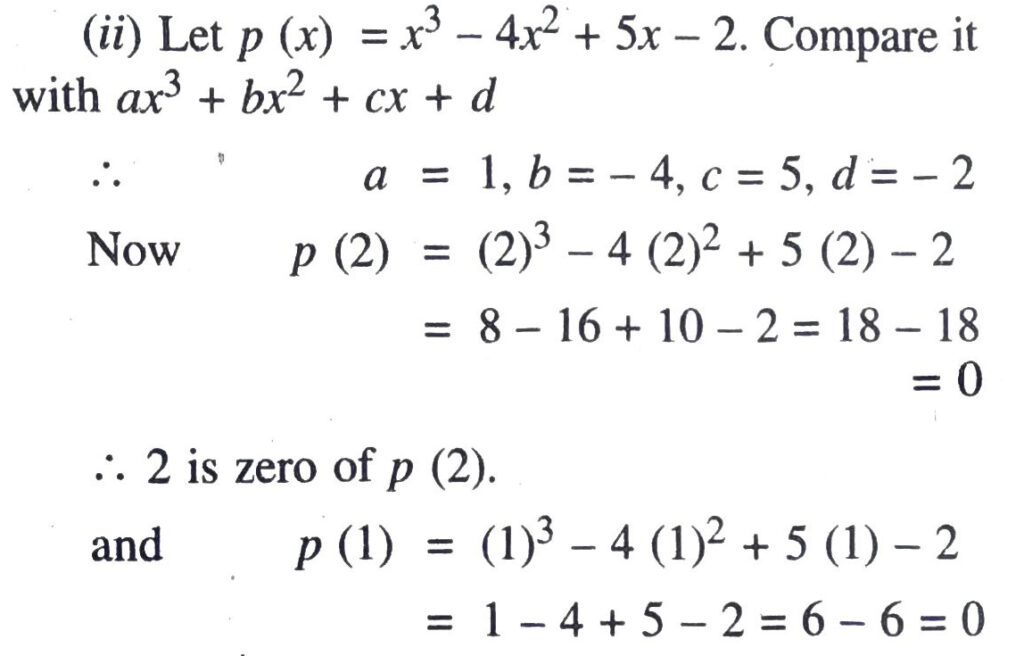
From above discussion, it is clear that 2, 1, 1 are the zeroes of given polynomial. Ans.
Let these zeroes are
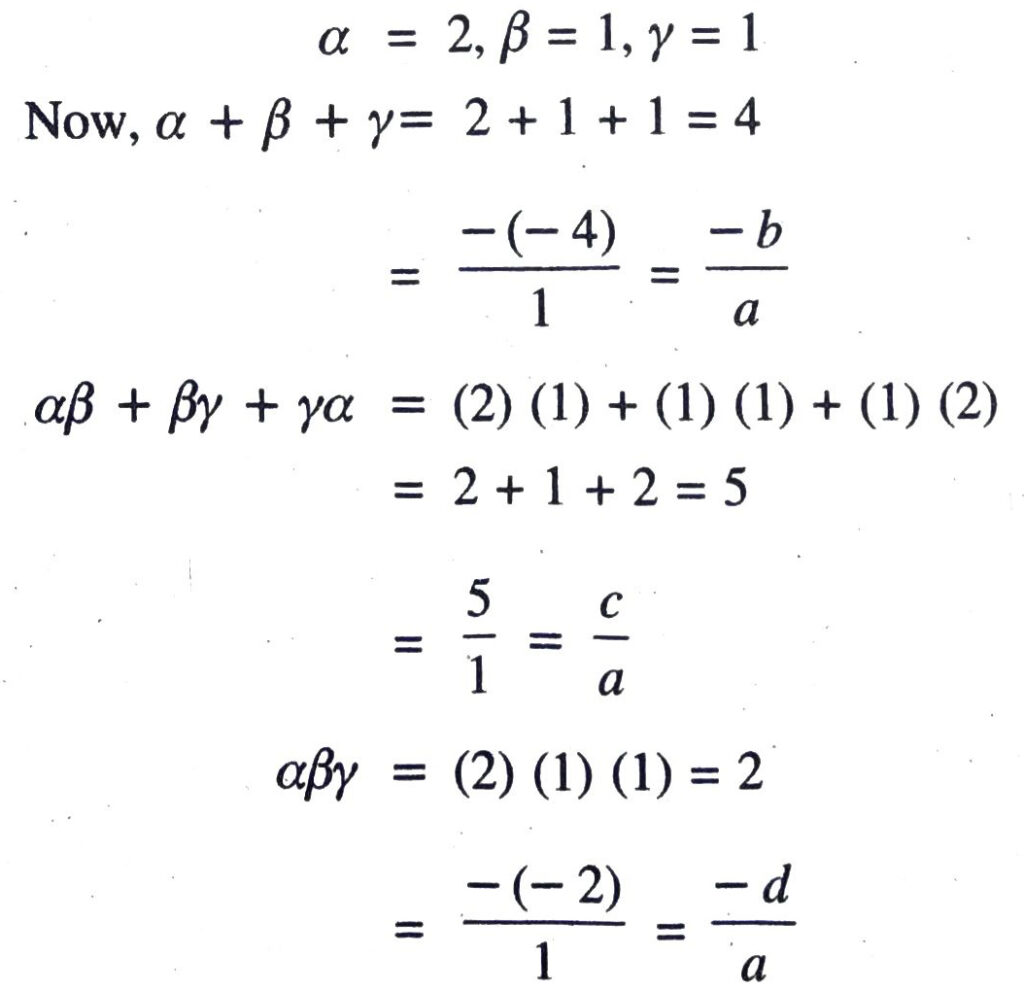
From above discussion, it is clear that there is a relationship between zeroes and coefficient.
Q. 2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, – 7, – 14 respectively.
Solution. The general expression of cubic polynomial are

For different values of k, we get different cubic polynomial.
Q. 3. If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
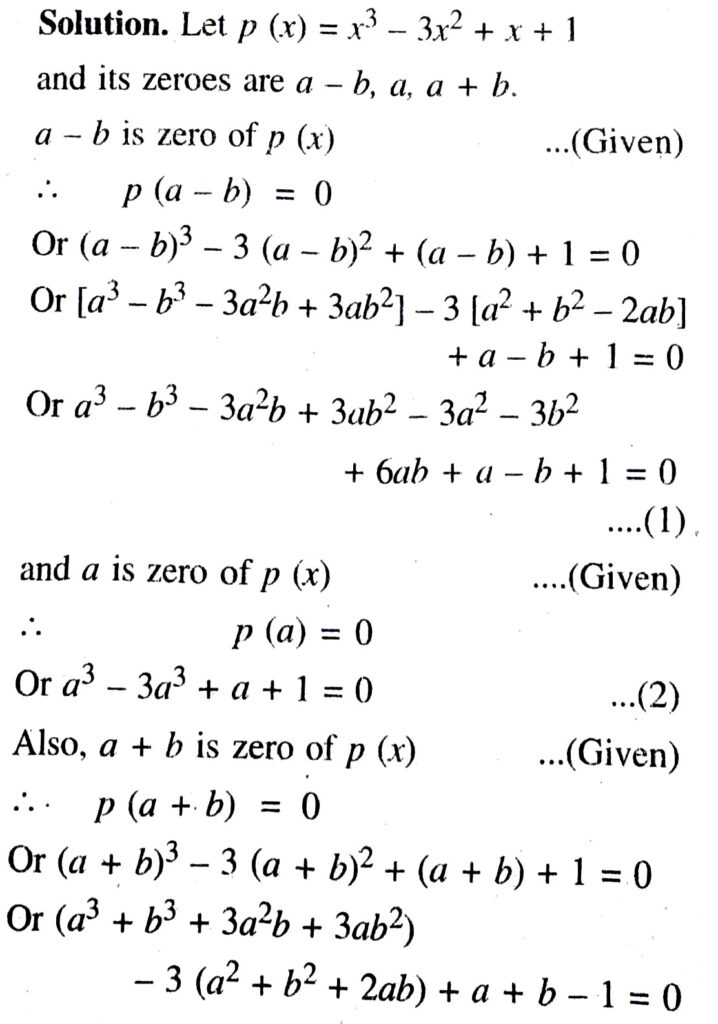
Or a³ + b³ + 3a²b + 3ab² – 3a² – 3b² – 6ab + a + b + 1 = 0 ….(3).
Adding (1) and (3), we get :
2a³ + 6ab² – 6a² – 6b² + 2a + 2 = 0
Or a³ + 3ab² – 3a² – 3b² + a + 1 = 0
Or (a³ – 3a³ + a + 1) + (3ab² – 3b²) = 0
Or 0 + 36² (a – 1) = 0 [Using (2)]
Or a – 1 = 0
Or a = 1 ….(4)
From (3) and (4), we get :
(1)³ + b³ + 3(1)²b + 3(1)b² – 3 (1)² – 3b² − 6 (1) b + 1 + b + 1 = 0
Or 1 + b³ + 3b + 36² – 3 – 3b² – 6b + b + 2 = 0
Or b³ – 2b = 0
Or b (b² – 2) = 0
Or b² – 2 = 0
Or b2 = 2
Or b = ±√2
Hence a = 1, b = ±√2 Ans.
Another Solution
Given that three zeroes of polynomial. x³ – 3x² + x + 1 are a – b, a, a + b respectively.
Now, sum of zeroes = (a – b) + a + (a + b)
= a – b + a + a +b
= 3a
But, sum of zeroes using coefficient
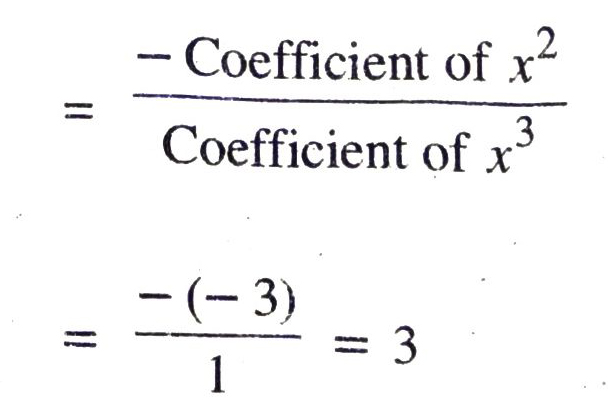
∴ 3a = 3 Or a = 1
Also, product of zeroes = (a – b). a. (a + b) = (a² – 6²) a
Putting the value of a, we get :
= (1² – b²). 1
= (1 – b²)
But, product of zeroes using coefficient

Q. 4. If two zeroes of the polynomial x4 – 6x³ – 26x² + 138x – 35 are 2 ± √3, find other zeroes.
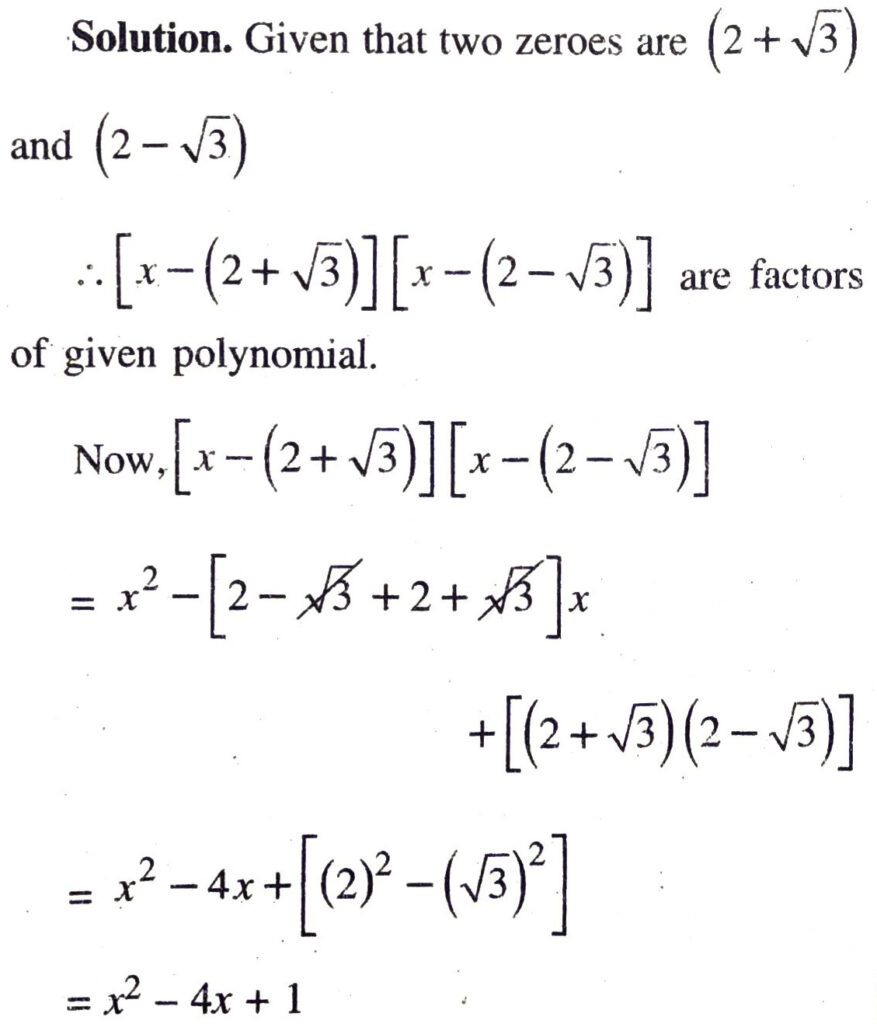
∴ (x² – 4x + 1) is factor of given polynomial.
Now, apply division algorithm to given polynomial and (x² – 4x + 1)
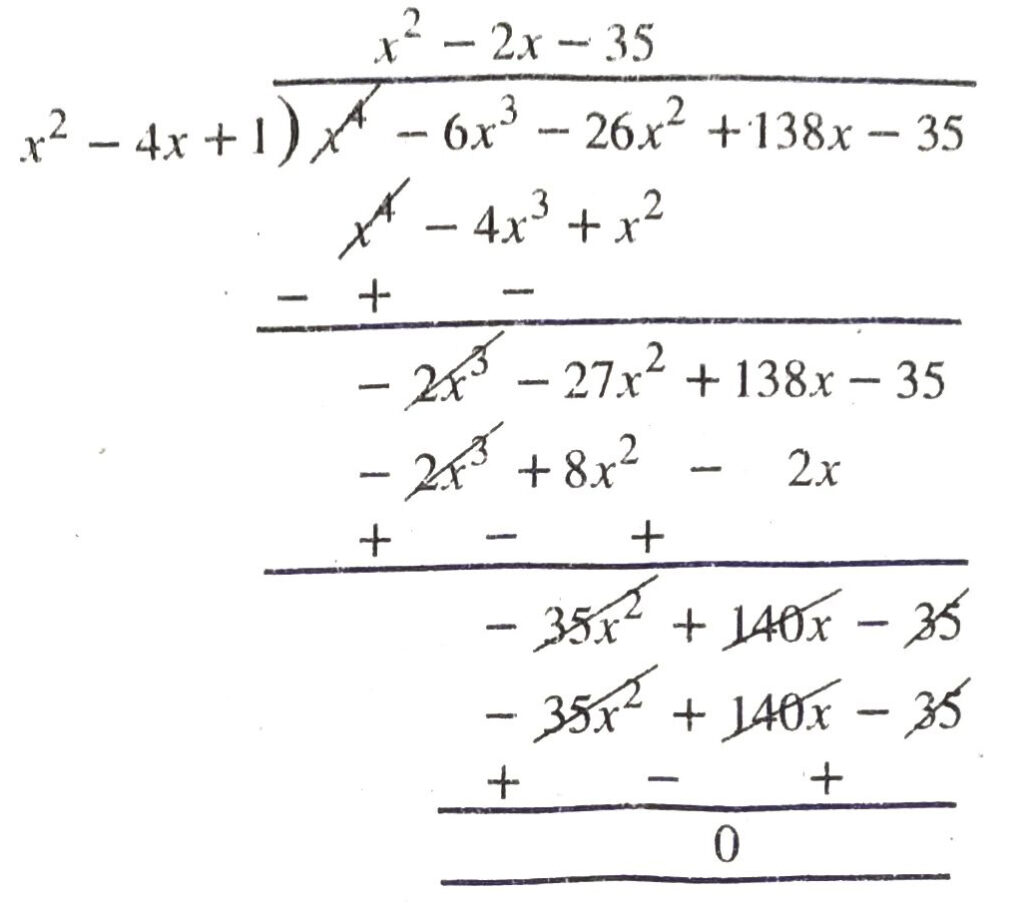
∴ x4 – 6x³ – 26x² + 138x − 35
= (x² – 4x + 1) (x² – 2x – 35)
= (x² − 4x + 1) [x² + 5x − 7x − 35)
S = -2, P = – 35
= (x² − 4x + 1) [x (x + 5) − 7 (x + 5)]
= (x² – 4x + 1) (x + 5) (x-7)
Now, other zeroes of polynomials are given by :
x + 5 = 0 Or x – 7 = 0
x = – 5 Or x = 7
∴ the zeroes of the given fourth degree polynomial are:
2+√3, 2 – √3, -5,7 Ans.
Q. 5. If the polynomial x4 – 6x³ + 16x2 – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution. Given that, polynomial
x4 – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k then remainder comes out to be x + a
So, first of all we divide,
x4 – 6x³ + 16x² – 25x + 10 with x² – 2x + k. and find quotient and remainder.

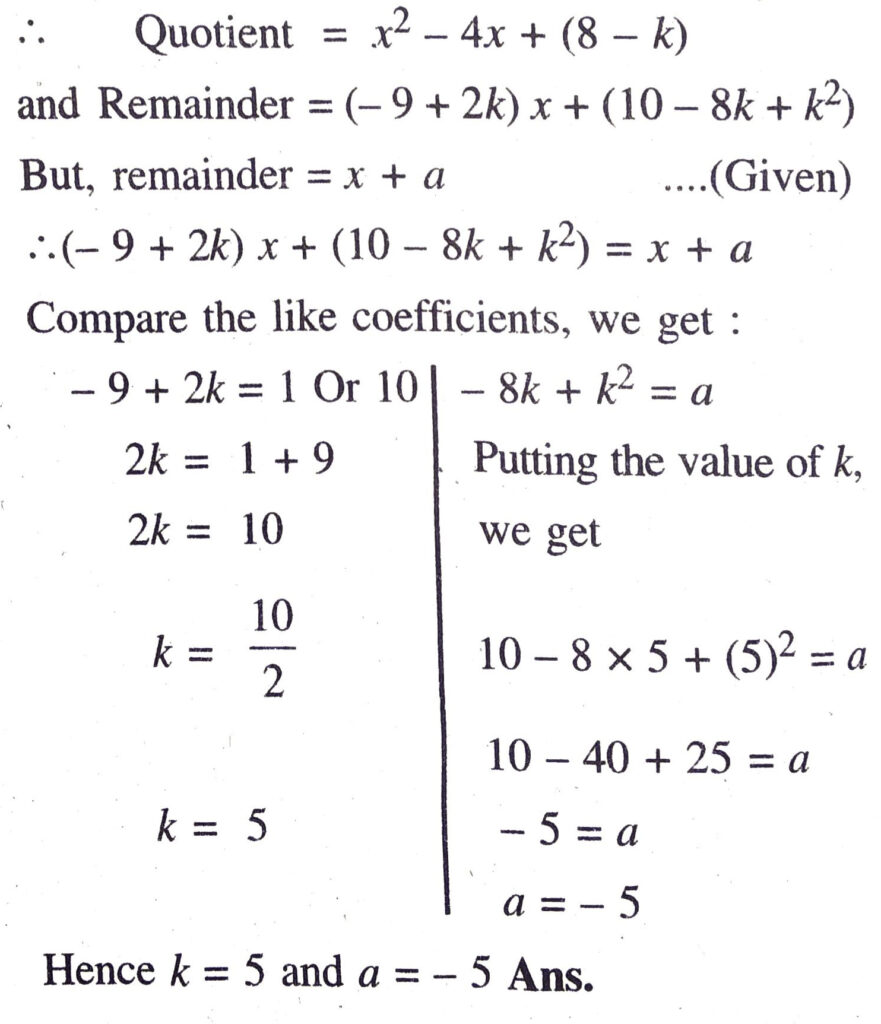
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here