JKBOSE 10th Class Maths Solutions chapter – 8 Introduction to Trigonometry
JKBOSE 10th Class Maths Solutions chapter – 8 Introduction to Trigonometry
J&K 10th Class Maths Solutions chapter – 8 Introduction to Trigonometry
Jammu & Kashmir State Board JKBOSE 10th Class Maths Solutions
INTRODUCTION
1. If a student is looking at the top of the Minar, a right angled can be imagined to be made, as shown below.
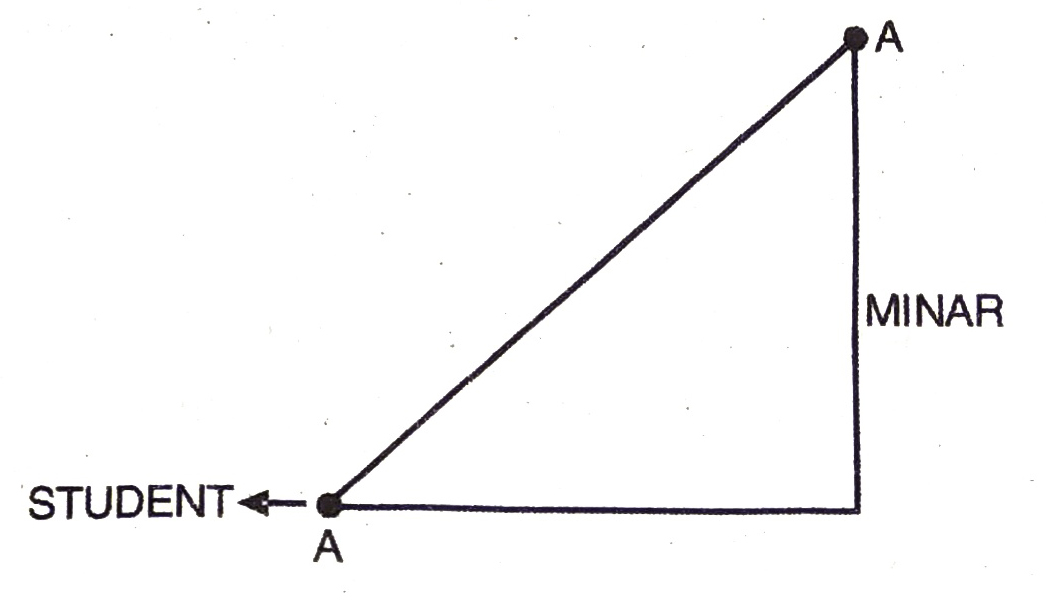
2. Suppose a girl is sitting on the balcony of her house located on the bank of a river. She is looking down at a flower pot placed on a stair of a temple situated nearby on the other bank of a river. A right triangle is made in this situation as shown below.
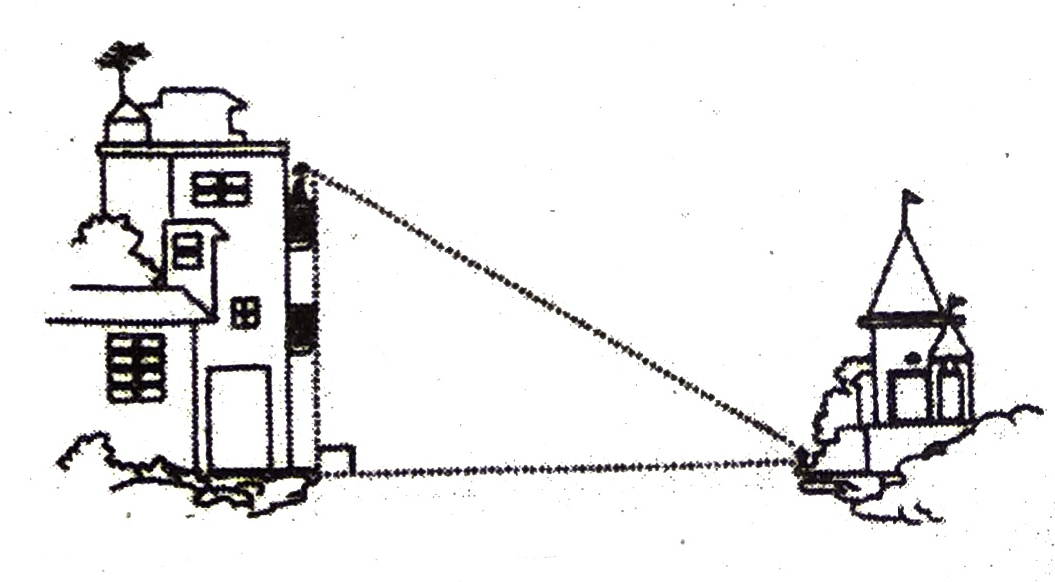
In all the situations given above, the distances or heights can be found by using some mathematical techniques, which come under a branch of mathematics called ‘trigonometry’. The word ‘trigonometry’ is derived from the Greek words ‘tri’ (meaning three), ‘gon’ (meaning sides), and ‘metron’ (meaning measure). In fact, trigonometry is the study of relationships between the sides and angles of a triangle.
In this Chapter, we will study some ratios of the sides of a right triangle with respect to its acute angles called trigonometric ratios of the angle. We will also define the trigonometric ratios for angles of measure 0° and 90°. We will I calculate trigonometric ratios for some specific angles and establish some identities involving these ratios called trigonometric identities.
TEXT BOOK EXERCISE 8.1
Q. 1. In ΔABC, right angled at B, AB = 24 cm; BC=7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution. Given that,
AB = 24 cm; BC = 7 cm; ∠B = 90°
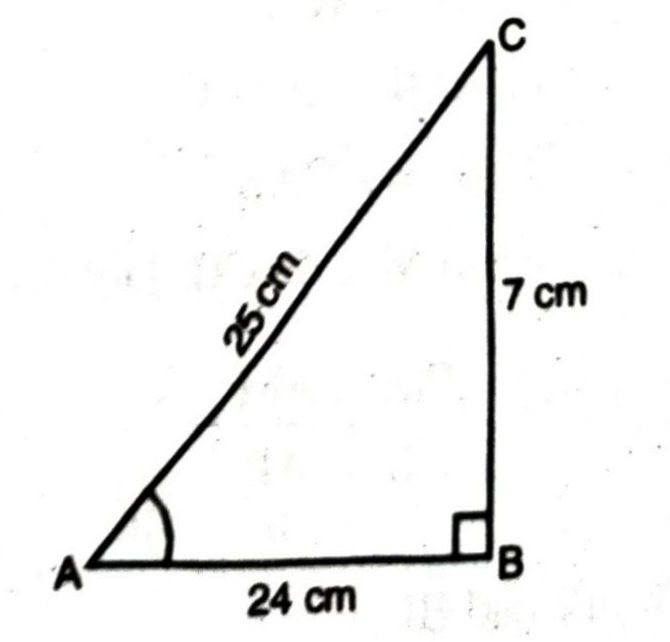
By using Pythagoras Theorem,
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49 = 625
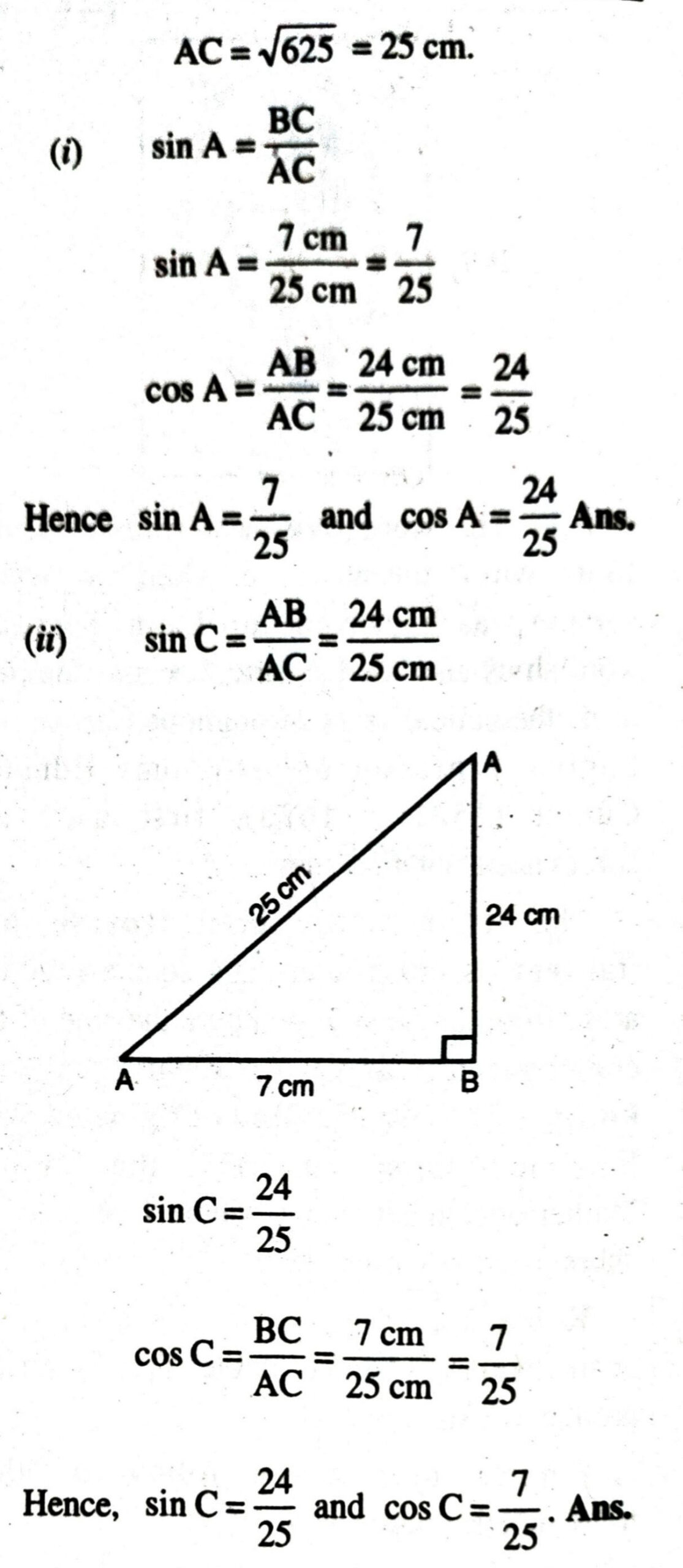
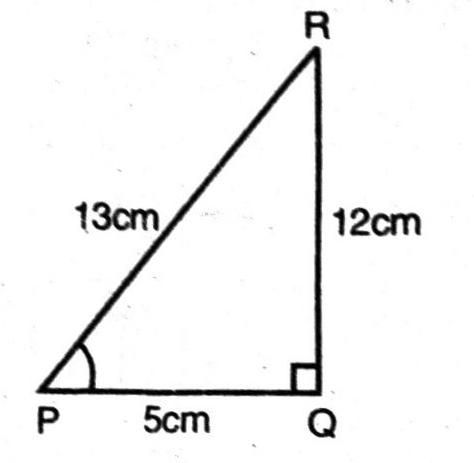
Q. 2. In fig., find tan P – cot R.
Solution. Hyp. PR = 13 cm
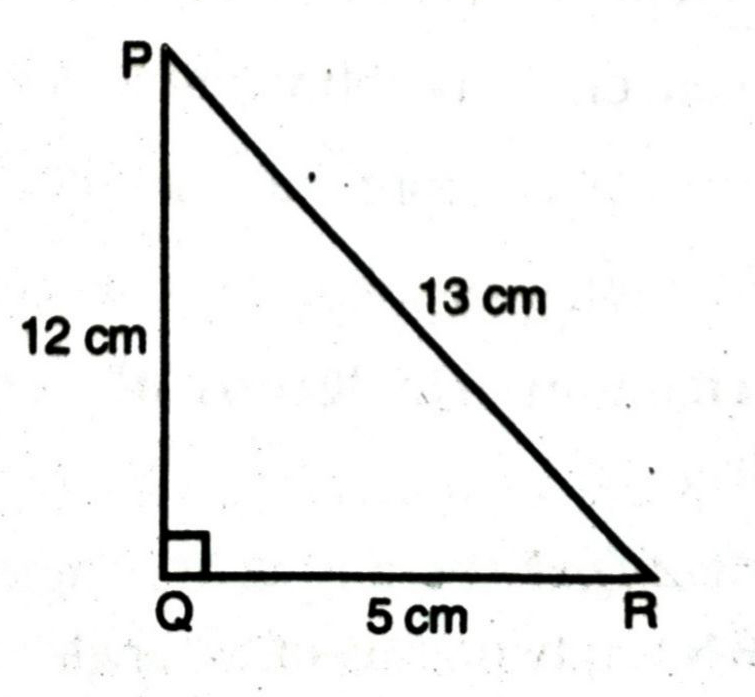
By using Pythagoras Theorem,
PR² = PQ² + QR²
or (13)² = (12)² + QR²
or 169 = 144 + (QR)²
or 169 – 144 = (QR)²
or 25 = (QR)²
or QR = ±√25
or QR = 5, – 5.
But QR = 5 cm.
[QR ≠ – 5, because side cannot be negative]
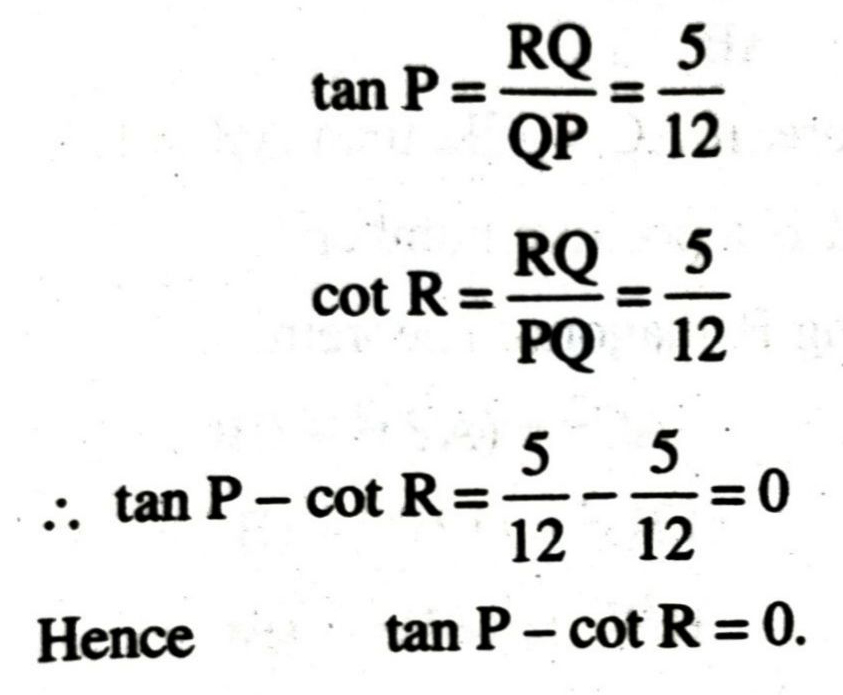
Q. 3. If sin A = 3/4 calculate cos A and tan A.
Solution. Let ABC be any triangle with right angle at B.
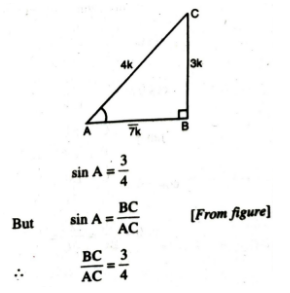
Therefore, if BC = 3K, then AC 4K, where K is a positive number.
By using Pythagoras Theorem,
AC² = AB² + BC²
or (4K)² = (AB)² + (3K)²
or 16K² = AB² + 9K²
or 16K² – 9K² = AB²
or 7K² =AB²
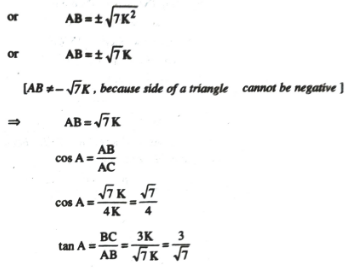
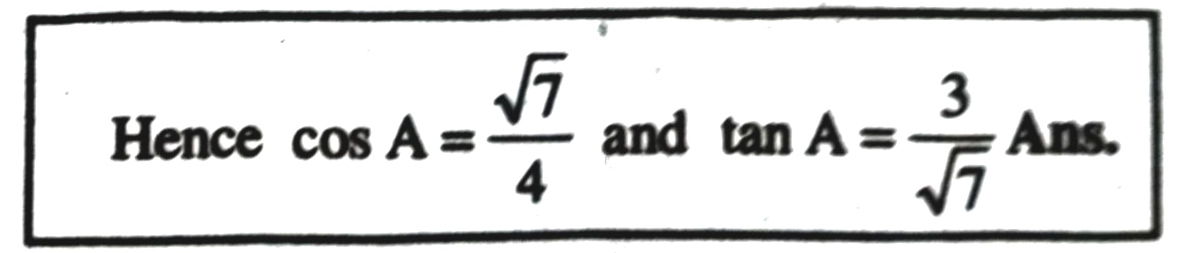
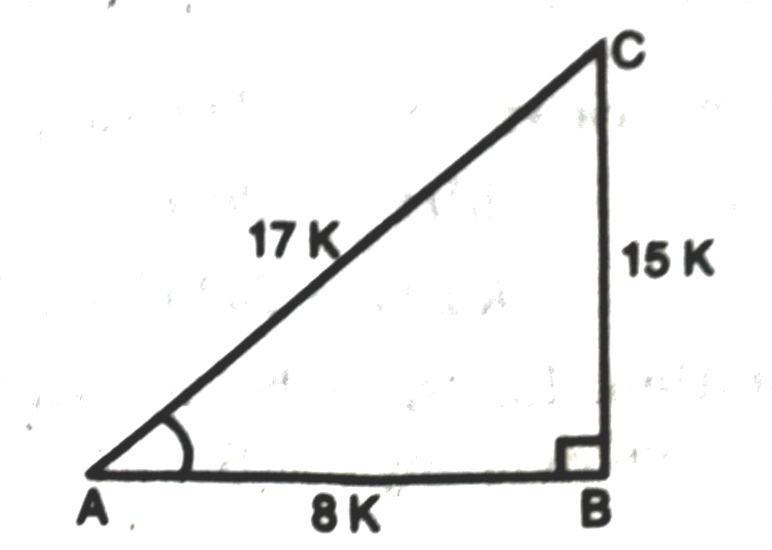
Q.4. Given 15 cot A = 8, find sin A and sec A.
Solution. Let ABC be any right angled triangle where A is an acute angle with right angle at B.

Q. 5. Given sec θ = 13/12 calculate all other trigonometric ratios.
Solution. Let ABC be any right angled triangle with right angle at B.
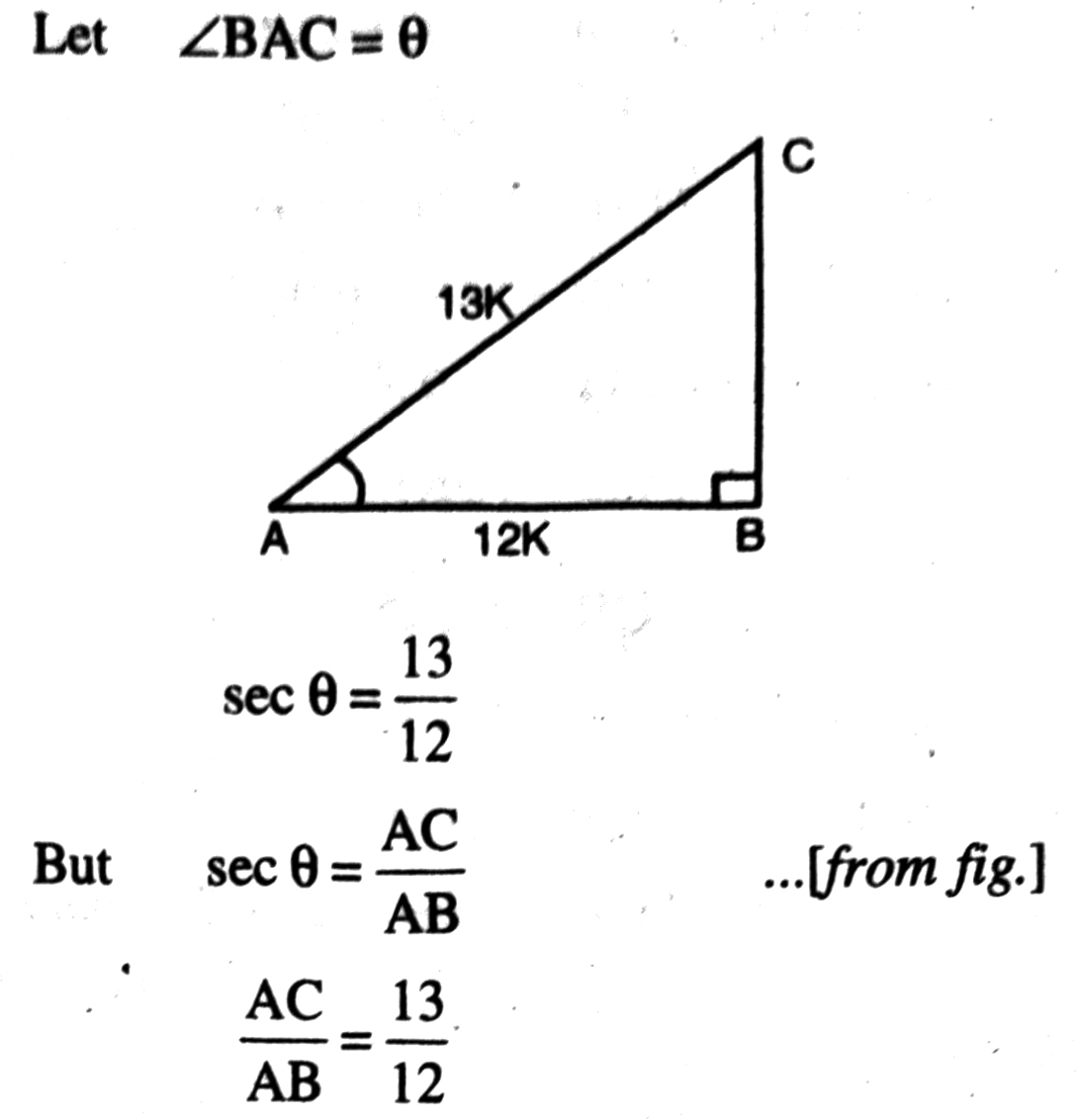
Therefore, if AC = 13k, then AB = 12k,
where k is a positive number.
By using Pythagoras Theorem,
AC² = (AB)² + (BC)²
or (13k)² = (12k)² + (BC)²
or 169k² = 144k² + (BC)²
or 169k² – 144k² = (BC)²
or (BC)² = 25k²

Q. 6. If ∠A and ∠B are acute angles such that cos A = cos B, show that ∠A = ∠B.
Solution. Let ABC be any triangle,
where ∠A and ∠B are acute angles. To find cos A and cos B.
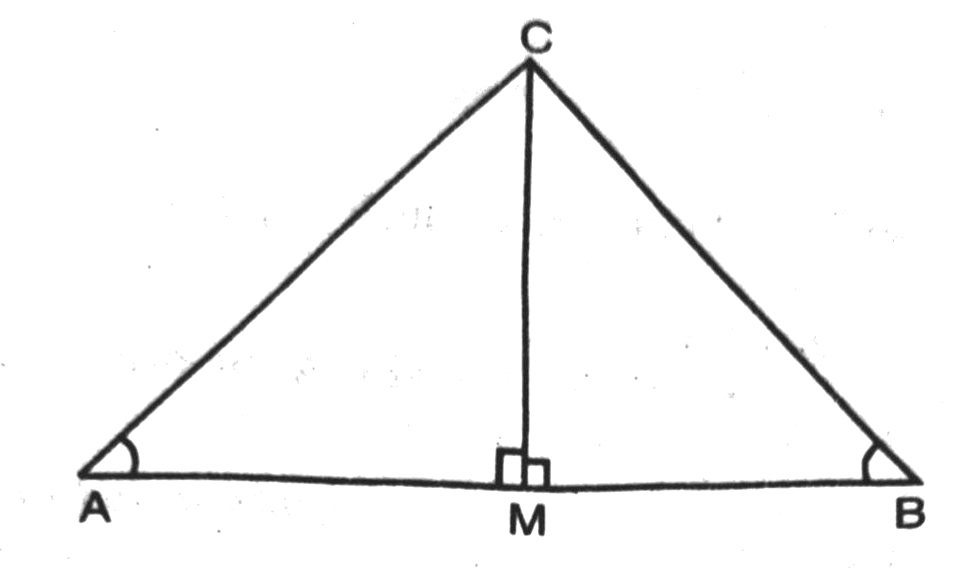
Draw CM ⊥ AB
∠AMC = ∠BMC = 90°
In right angled ΔAMC,

Q. 7. If cot θ = 7/8 evaluate
(ii) cot² θ.
Solution. (i) ∠ABC = θ.
In right angled triangle ABC with right angle at C.
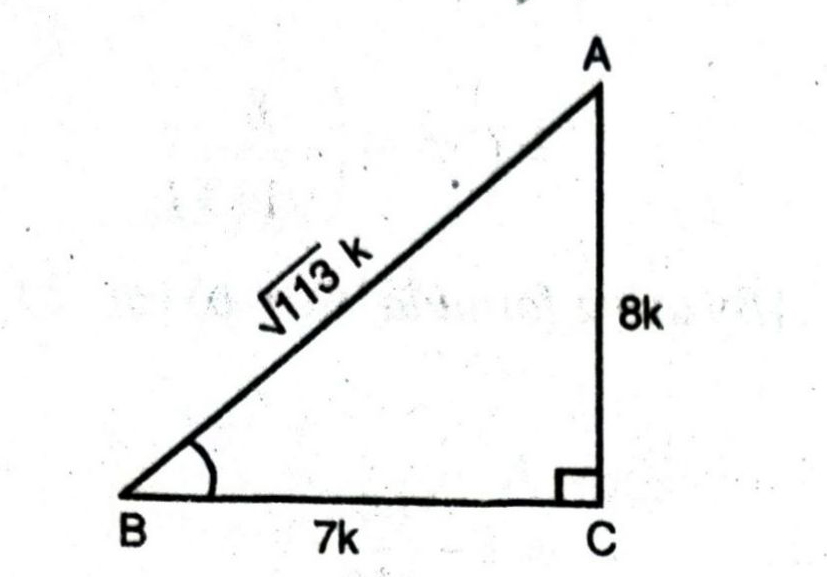

Therefore, if BC = 7k, then AC = 8k
where k is a positive number
By using Pythagoras Theorem,
AB² = (BC)² + (AC)²
or (AB)² = (7k)² + (8k)²
or (AB)² = 49k² + 64k²
or (AB)² = 113k²
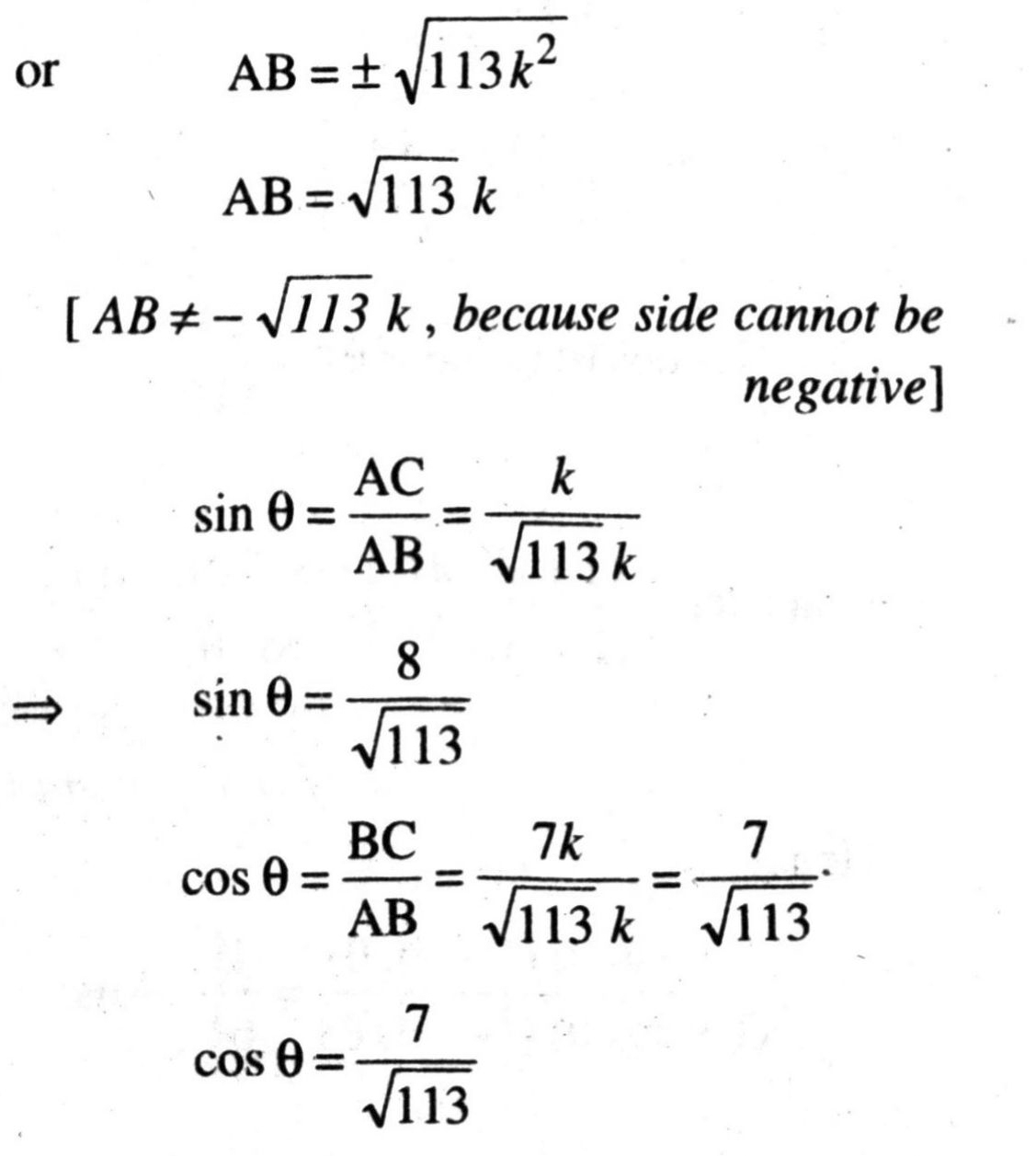
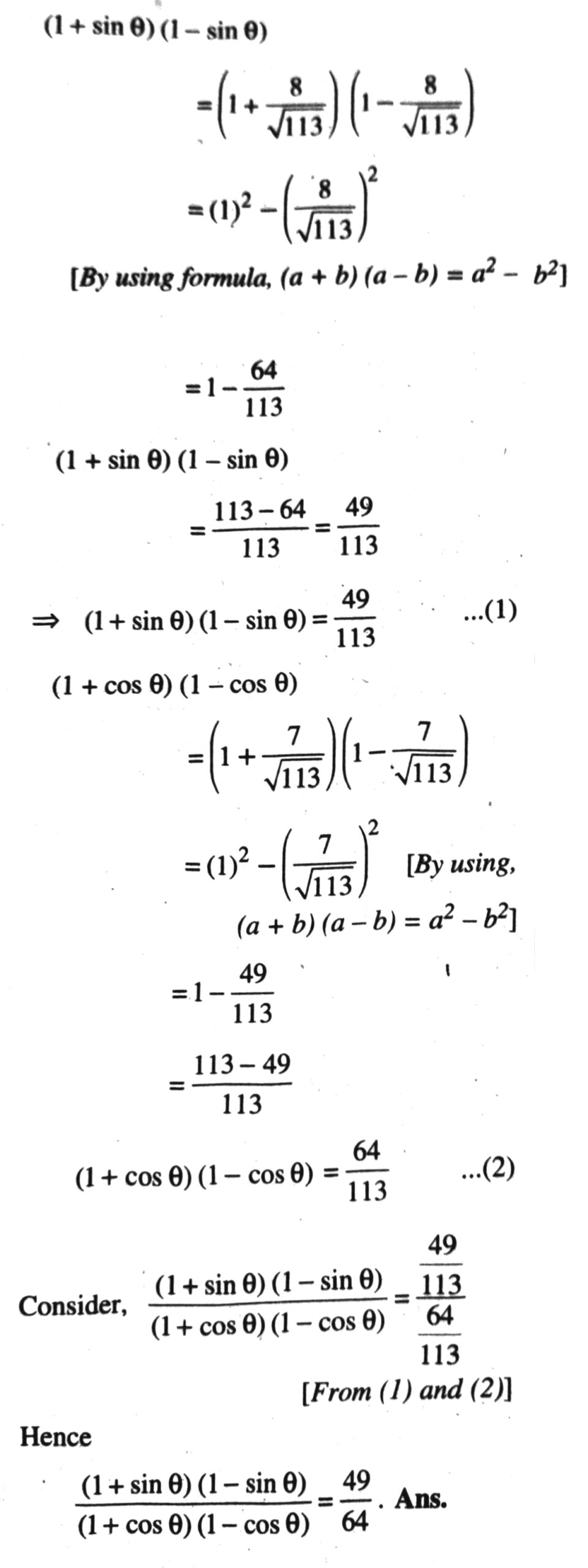
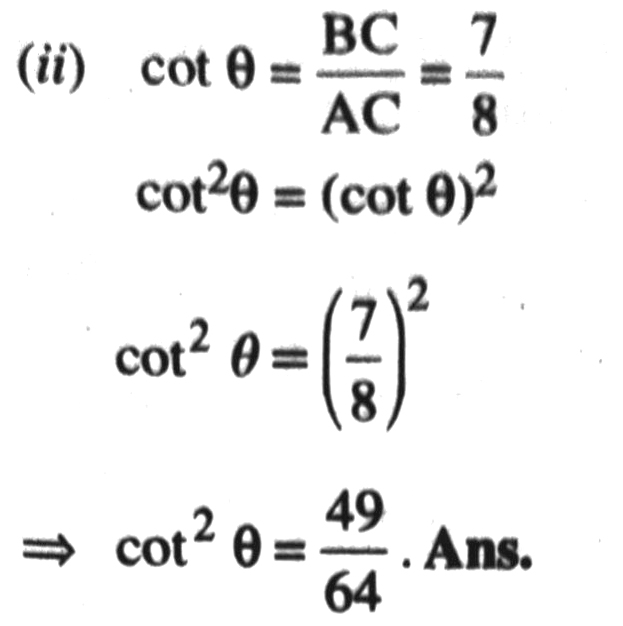
Q. 8. If 3 cot A = 4 check whether.
Solution. Let ABC be a right angled triangle with right angled at B.
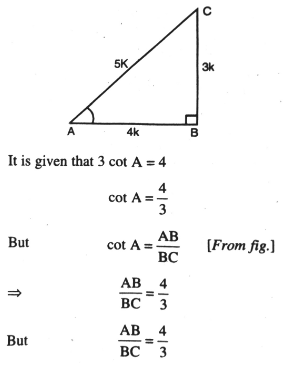
⇒ If AB = 4k then, BC = 3k where k is a positive number
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16k² + 9k²
(AC)² = 25k²
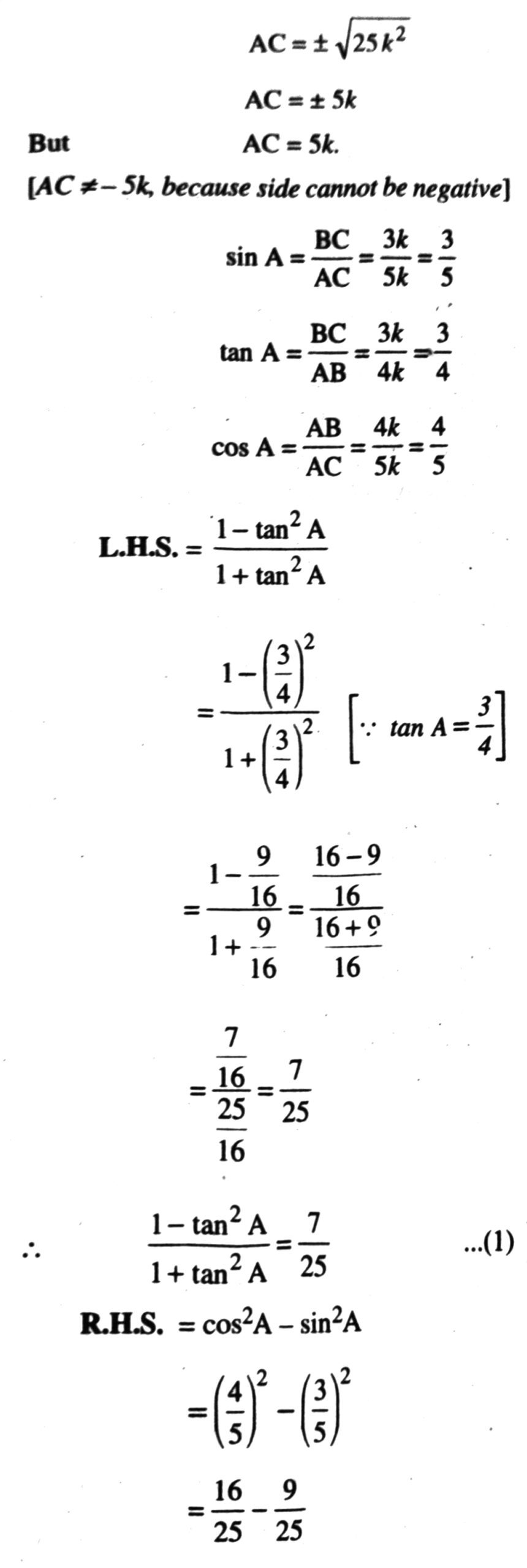
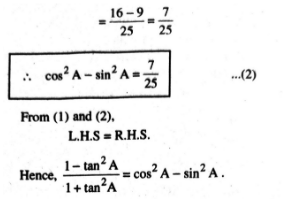
Q. 9. In triangle ABC, right angled at B, if tan A= 1/√3 Find the value of :
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
Solution. (i) Given: ΔABC with right angled at B
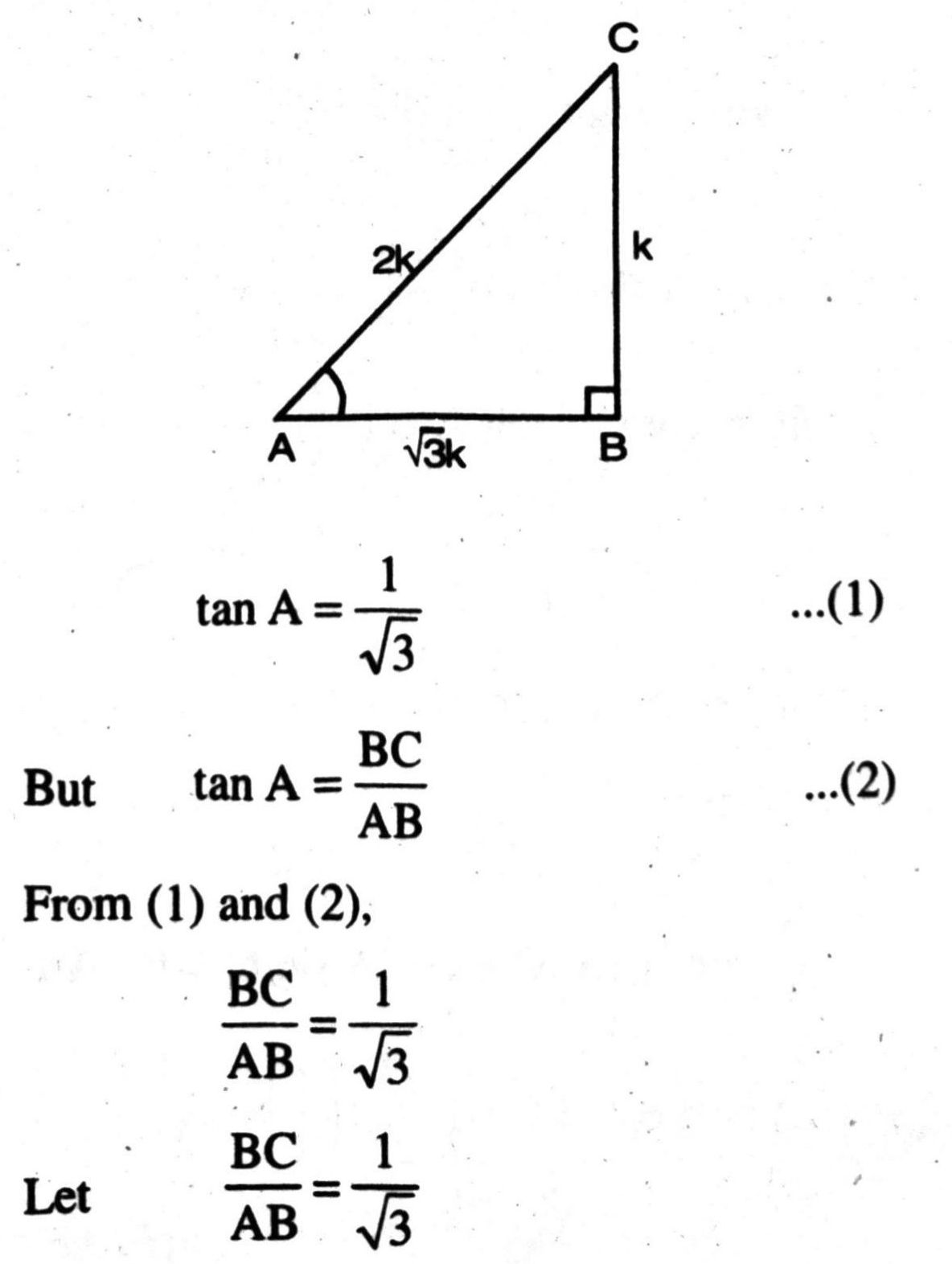
If BC = k then AB = √3k
where k is a positive number.
In right angled triangle ABC,
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
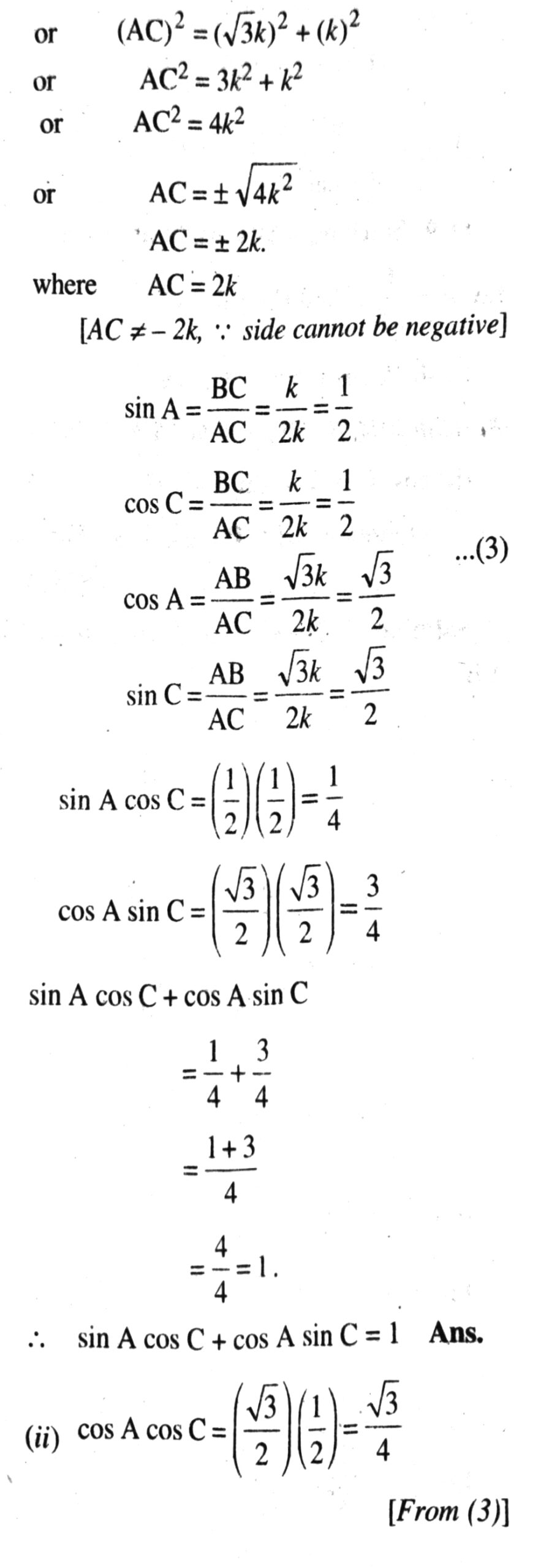
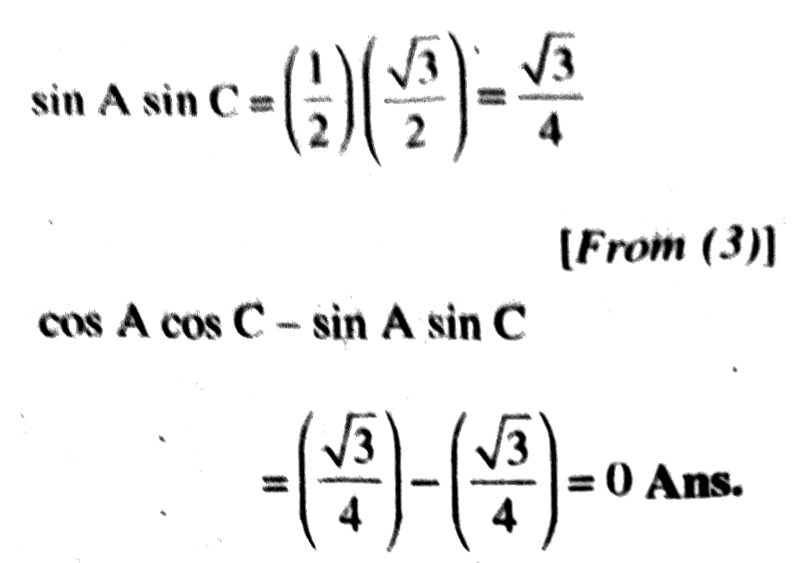
Q. 10. In ΔPQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution. Given: ΔPQR, right angled at Q
PR + QR = 25 cm
PQ = 5 cm
In right angled triangle PQR
By using Pythagoras Theorem,
(PR)² = (PQ)² + (RQ)²
or (PR²) = (5)² + (RQ)²
[∵ PR + QR = 25
QR = 25 – PR]
or (PR)² = 25 + [25 – PR]²
or (PR)² = 25 + (25)² + (PR)² – 2 × 25 × PR
or (PR)² = 25 + 625 + (PR)² – 50 PR
or (PR)² – (PR)² + 50 PR = 650
or 50 PR = 650

Q. 11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii) cos A is abbreviation used for cosecant of angle A.
(iv) cot A is product of cot and A.
(v) sin θ = 4/3 for some angle θ.
Solution. (i) False;
∵ tan 60° = √3 =1 · 732 > 1.
(ii) True; sec A = 12/5 = 2 · 40 > 1.
∵ Sec A is always greater than 1.
(iii) False;
Because cos A is used for cosine A.
(iv) False;
Because cot A is cotangent of the angle A not the product of cot and A.
(v) False; sin θ =4/3 = 1 · 666 > 1
Because sin θ is always less than 1.
TEXT BOOK EXERCISE 8.2
Q. 1. Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°

Solution. (i) sin 60° cos 30° + sin 30° cos 60°
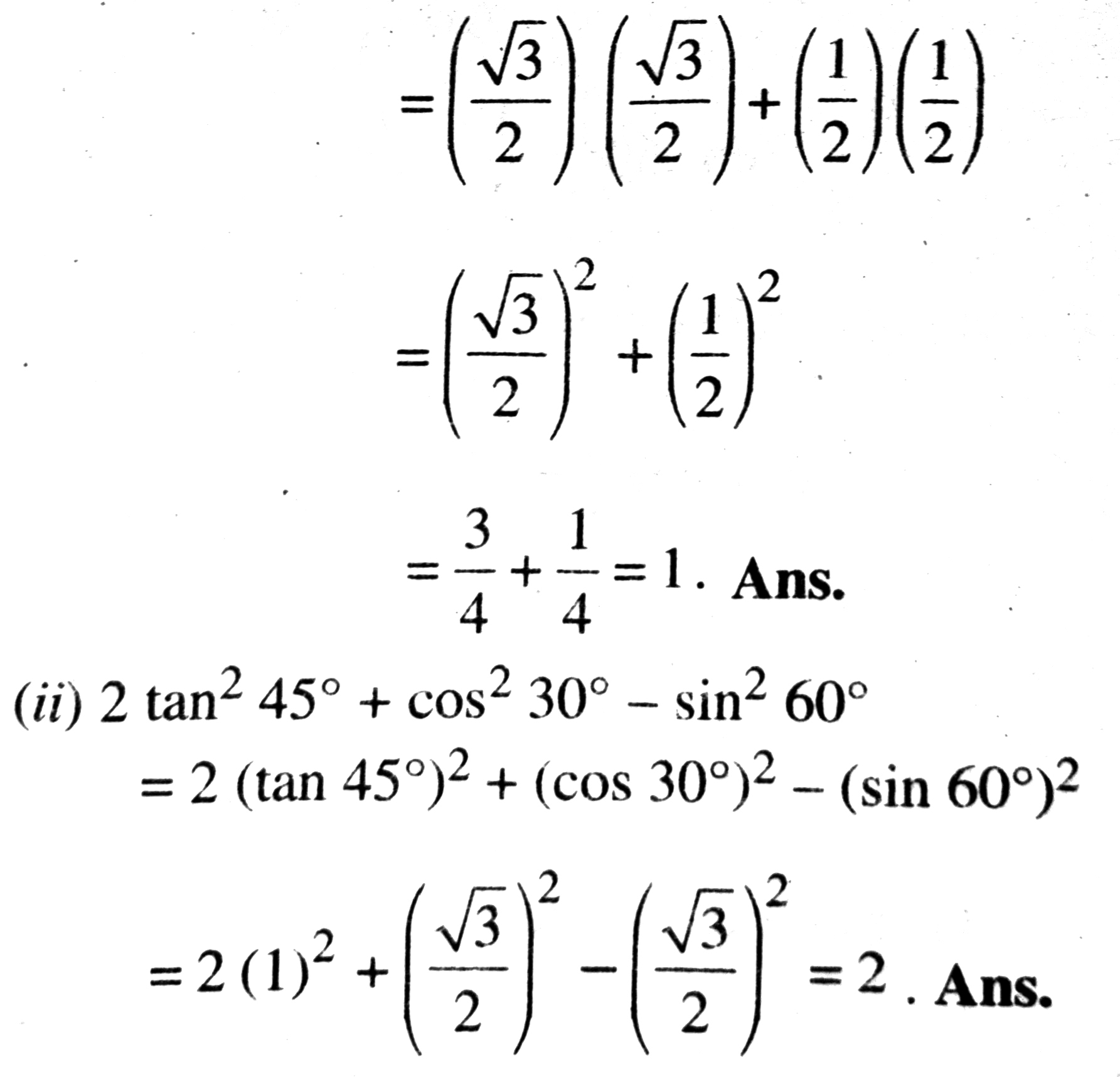
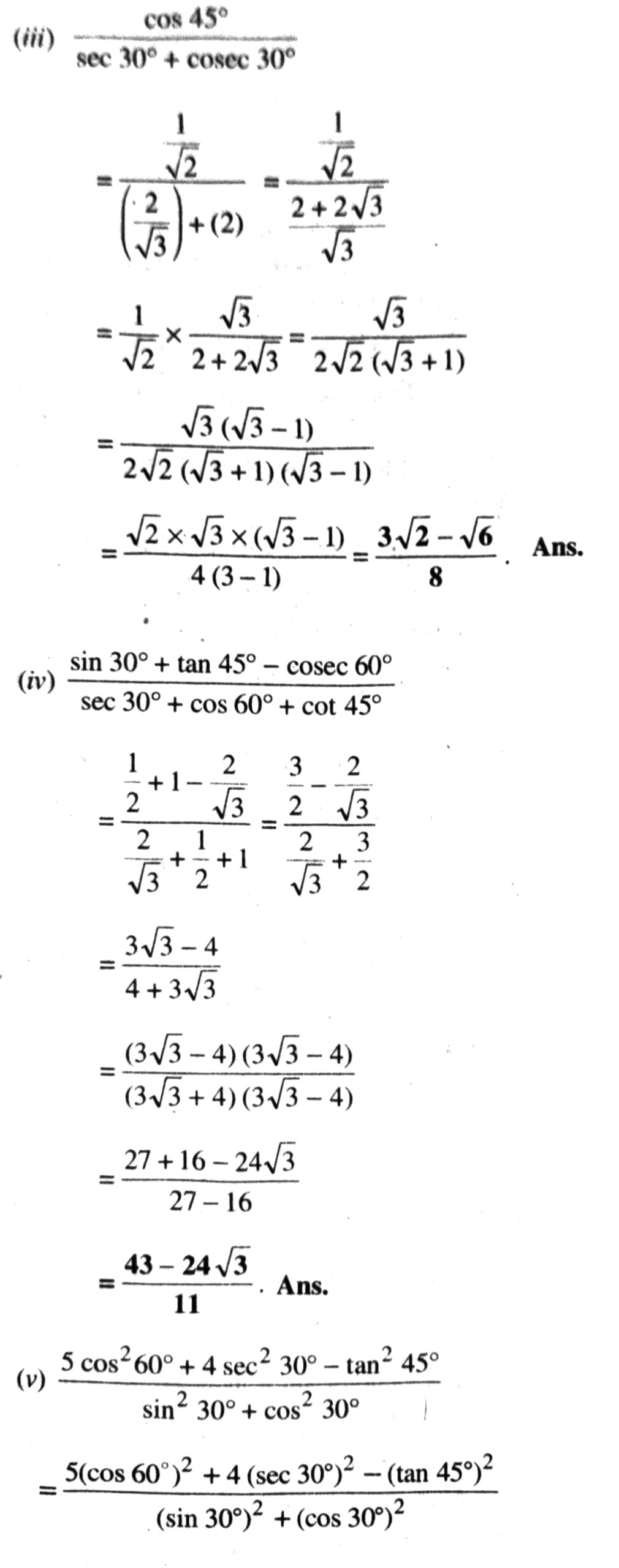

Q. 2. Choose the correct option and justify your choice.

So, correct answer is (A). Ans.
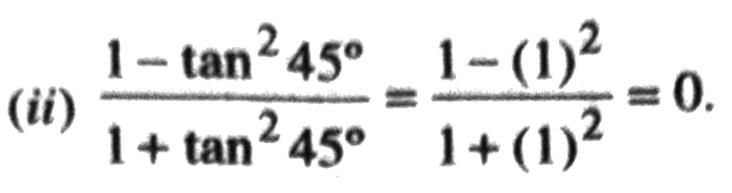
So, correct answer is (D).
(iii) Here when A = 90°
L.H.S. = sin 2A = sin 0° = 0
and R.H.S. = 2 sin A = 2 sin 0°
= 2 × 0 = 0
∴ Option (A) is correct. Ans.
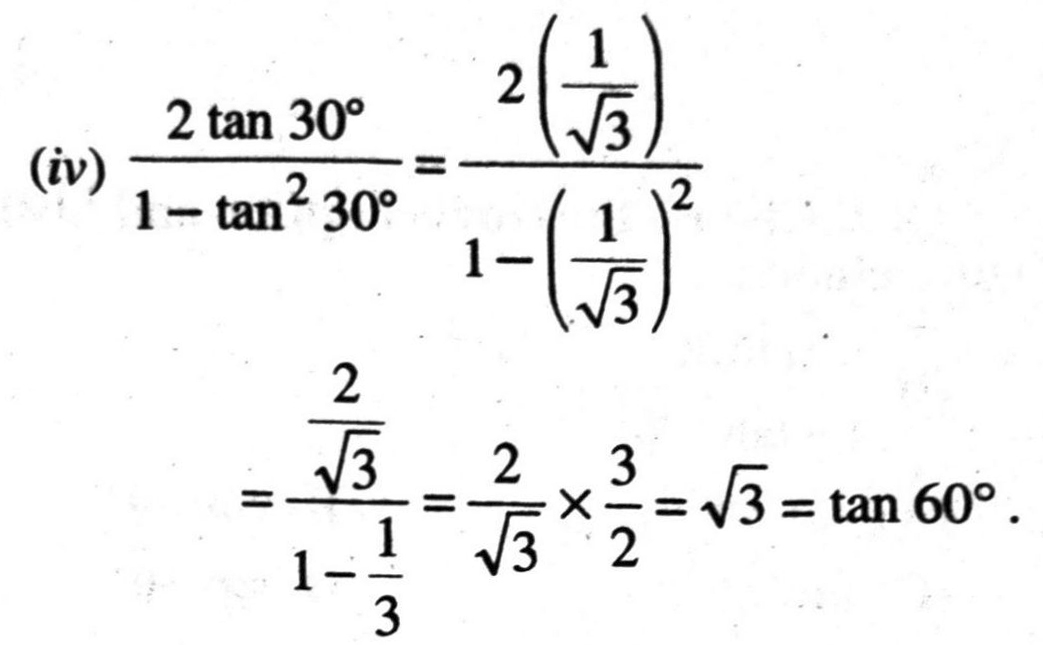
Option (A) is correct. Ans.
Q. 3. If tan (A + B) = √3 and tan (A – B) = 1/√3; 0° ∠A + B ≤ 90°; A > B, find A and B.

Put value of A = 45° in (1)
45° + B = 60°
B = 60° – 45°
B = 15°
Hence A = 45° and B = 15° Ans.
Q. 4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases
(iii) The value of cos θ increases as θ increases
(iv) sin θ = cos θ for all value of θ.
(v) cot A is not defined for A = 0°.
Solution. (i) False.
when A = 60°, B = 30°
L.H.S. = sin (A + B) = sin (60° + 30°)
= sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
i.e. L.H.S. ≠ R.H.S.
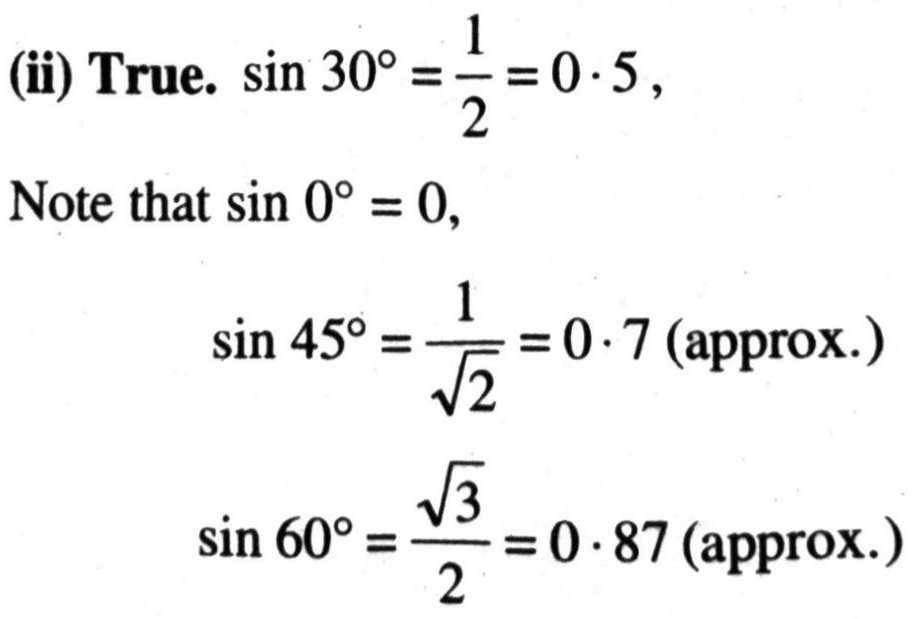
and sin 90° = 1
i.e. value of sin θ increases as θ increases from 0° to 90°.
(iii) False
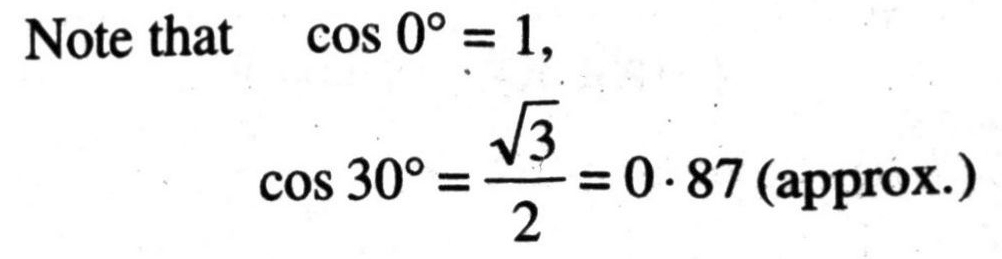

TEXT BOOK EXERCISE 8.3
Q. 1. Evaluate :

(iii) cos 48° – sin 42°
= cos (90° – 42°) – sin 42°
[ ∵ cos (90°- θ) = sin θ]
= sin 42° – sin 42° = 0. Ans.
(iv) cosec 31° – sec 59°.
= cosec 31° – sec (90° – 31°)
= cosec 31°- cosec 31°
[∵ sec (90° – θ) = cosec θ]
= 0. Ans.
Q. 2. Show that :
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52°- sin 38° sin 52° = 0
Solution. (i) L.H.S.
= tan 48° tan 23° tan 42° tan 67°
= tan 48° × tan 23° × tan (90° – 48°) × tan (90° – 23°)
= tan 48° × tan 23° × cot 48° × cot 23°
= tan 48° × tan 23° × 1/tan 48° × 1/tan 23° = 1
∴ L.H.S. = R.H.S.
(ii) L.H.S.= cos 38° cos 52° – sin 38° sin 52°
= cos 38° × cos (90° – 38°) – sin 38° × sin (90° – 38°)
= cos 38° × sin 38° – sin 38° × cos 38°
= 0
∴L.H.S. = R.H.S.
Q. 3. If tan 2A = cot (A – 18°) where 2A is an acute angle, find the value of A.
Solution. Given: tan 2A = cot (A – 18°)
⇒ cot (90° – 2A) = cot (A – 18°)
[∵ cot (90°- θ) = tan θ]
⇒ 90° – 2A = A – 18°
⇒ 3A = 108º
⇒ A = 36⁰.
Q. 4. If tan A = cot B, prove that A + B = 90°.
Solution. Given that: tan A = cot B
⇒ tan A = tan (90°- B)
[∵ tan (90° – θ) = cot θ]
⇒ A = 90° – B
⇒ A + B = 90°.
Q. 5. If sec 4A = cosec (A -20°), where 4A is an acute angle, find the value of A.
Solution. Given that : sec 4A = cosec (A – 20°)
⇒ cosec (90°- 4A) = cosec (A -20°)
[∵ cosec (90°- θ) = sec θ]
⇒ 90° – 4A = A – 20°
⇒ 5A = 110°
⇒ A = 22°.
Q. 6. If A, B and C interior angles of a triangle ABC, then show that :
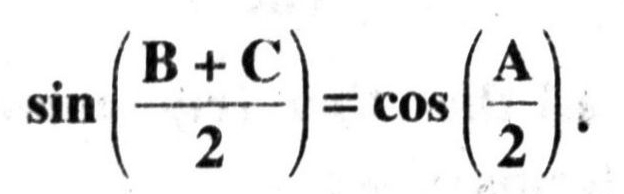
Solution. Since, A, B and C are interior angles of a triangle
∴ A+B+C = 180°
[Sum of three angles of a triangle is 180°]
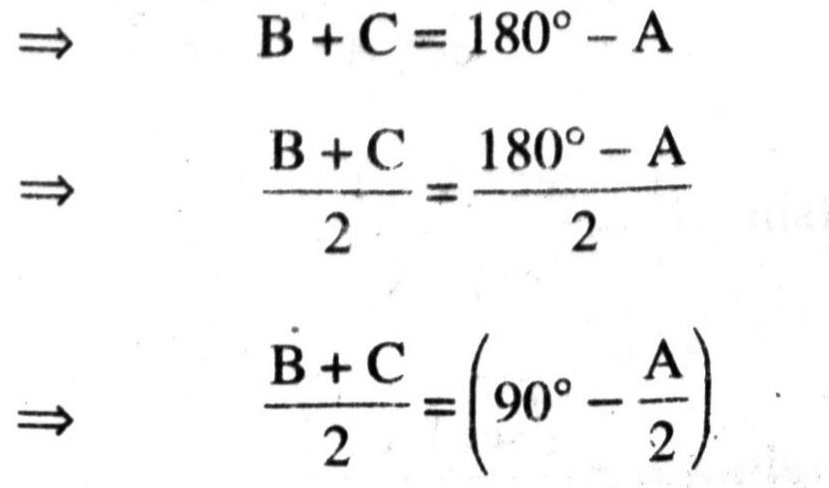
Taking sin on both sides, we get
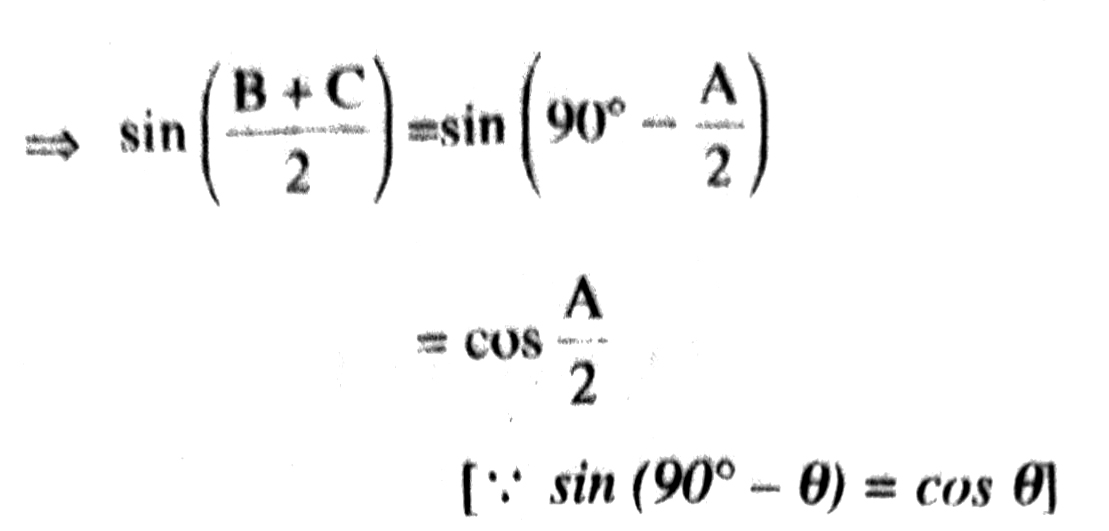
Q. 7. Express sin 67° + cos 75° in terms of Trigonometric ratios of angles between 0° and 45°.
Solution. Given that: sin 67° + cos 75°
= sin (90° -23°) + cos (90° -15°)
= cos 23° + sin 15°
[∵ sin (90°- θ) = cos θ and cos (90° – θ) = sin θ]
TEXT BOOK EXERCISE 8.4
Q. 1. Express the trigonometric ratios of sin A, sec A and tan A in terms of cot A.
Solution. By using Identity,
cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² A
⇒ (cosec A)² = cot² A + 1
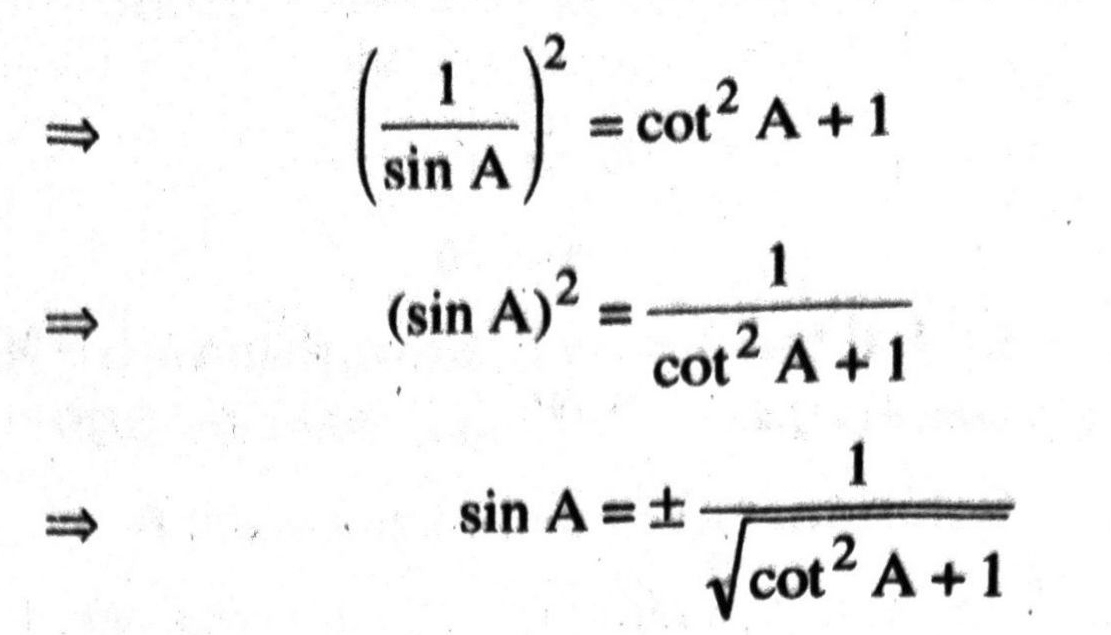
We reject negative values of sin A for acute angle A.
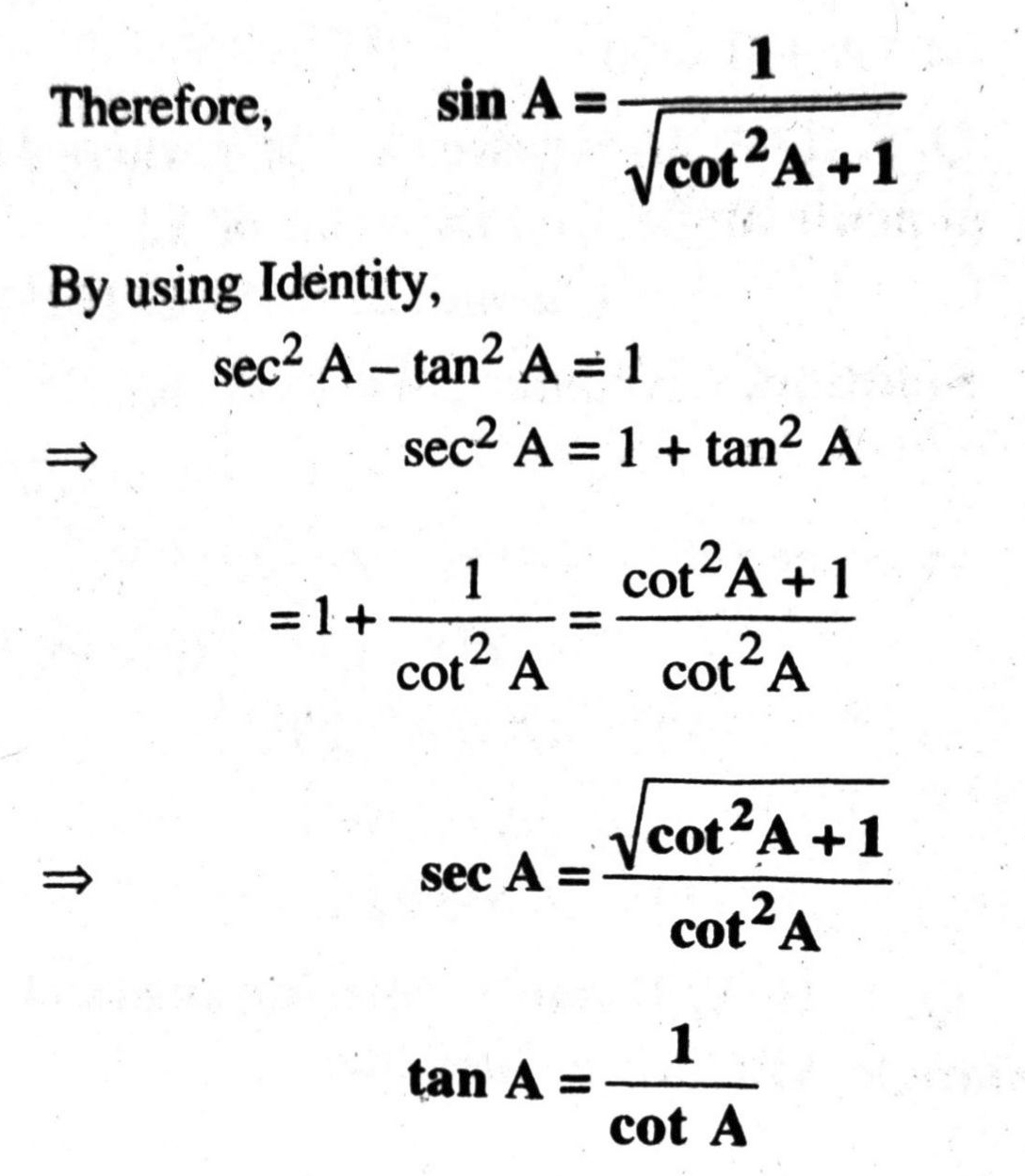
Q. 2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution. By using Identity,
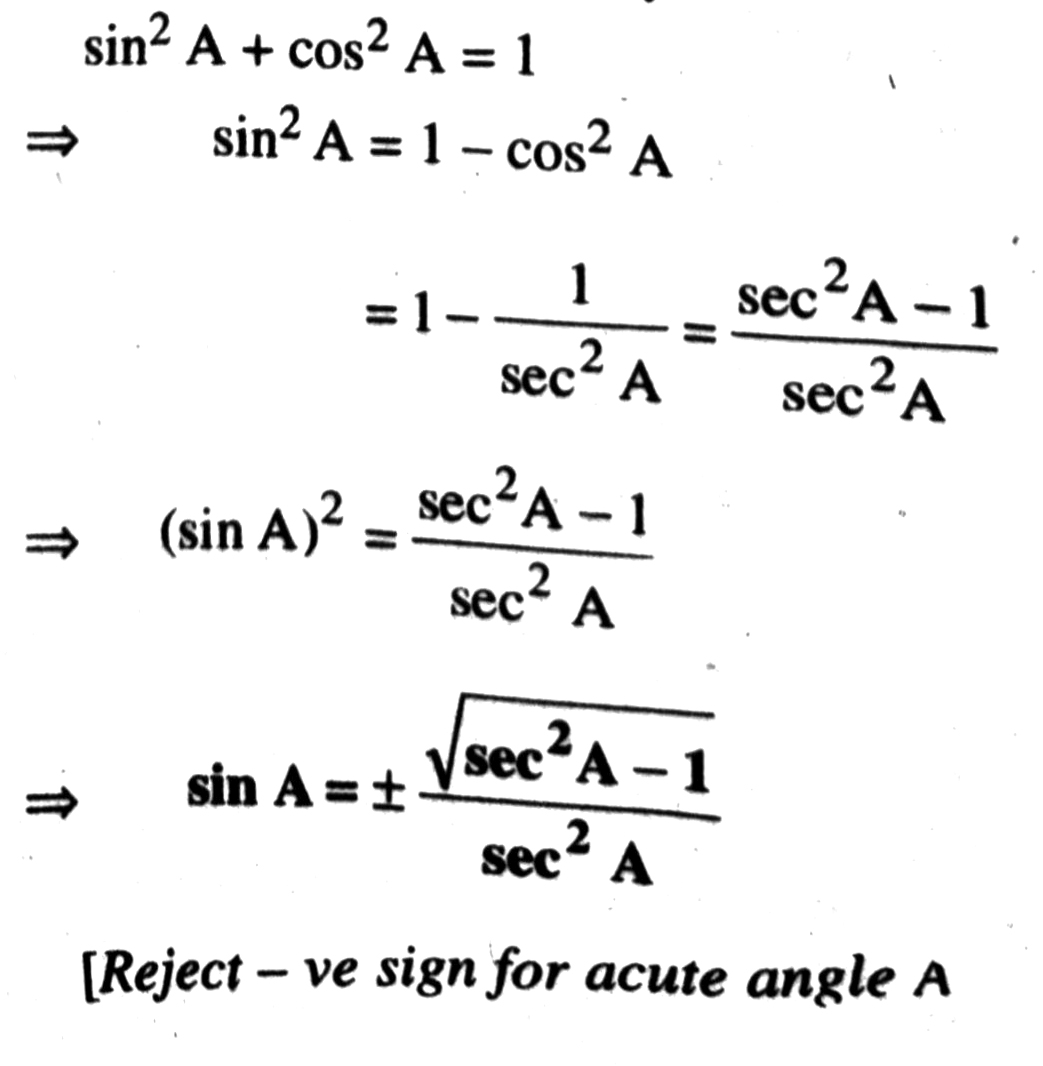

Q. 3. Evaluate :

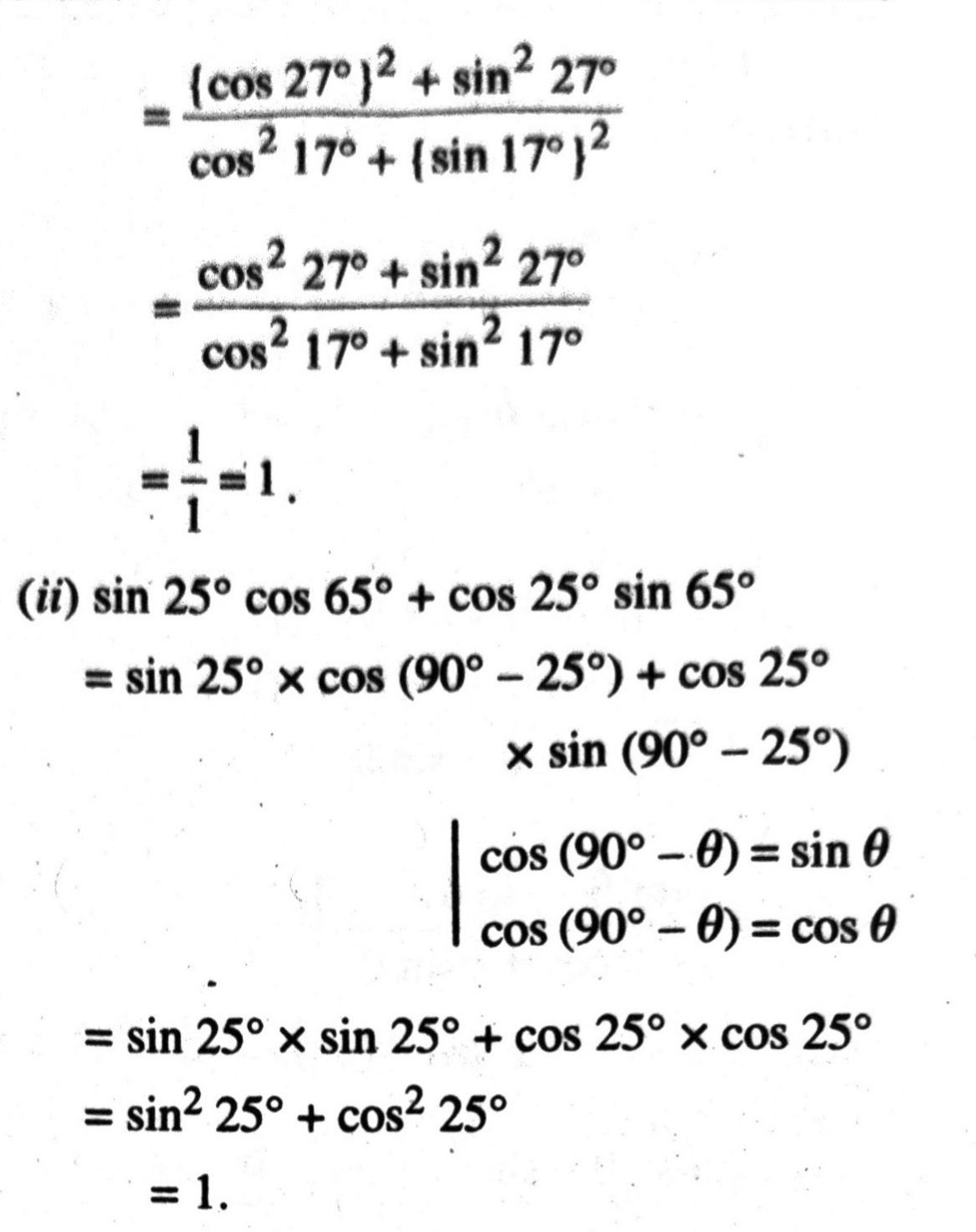
Q. 4. Choose the correct option. Justify your choice:
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0.
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) -1.
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A.
Solution. (i) Consider, 9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 × 1 = 9.
Option (B) is correct. Ans.
(ii) Consider, (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

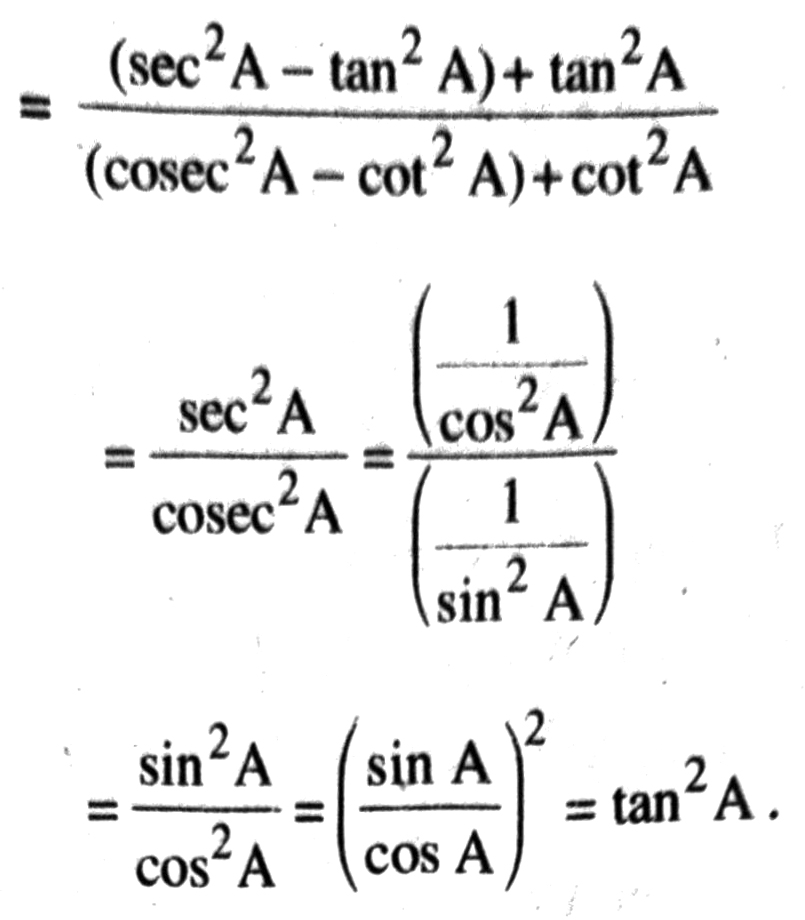
Option (D) is correct. Ans.
Q. 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.


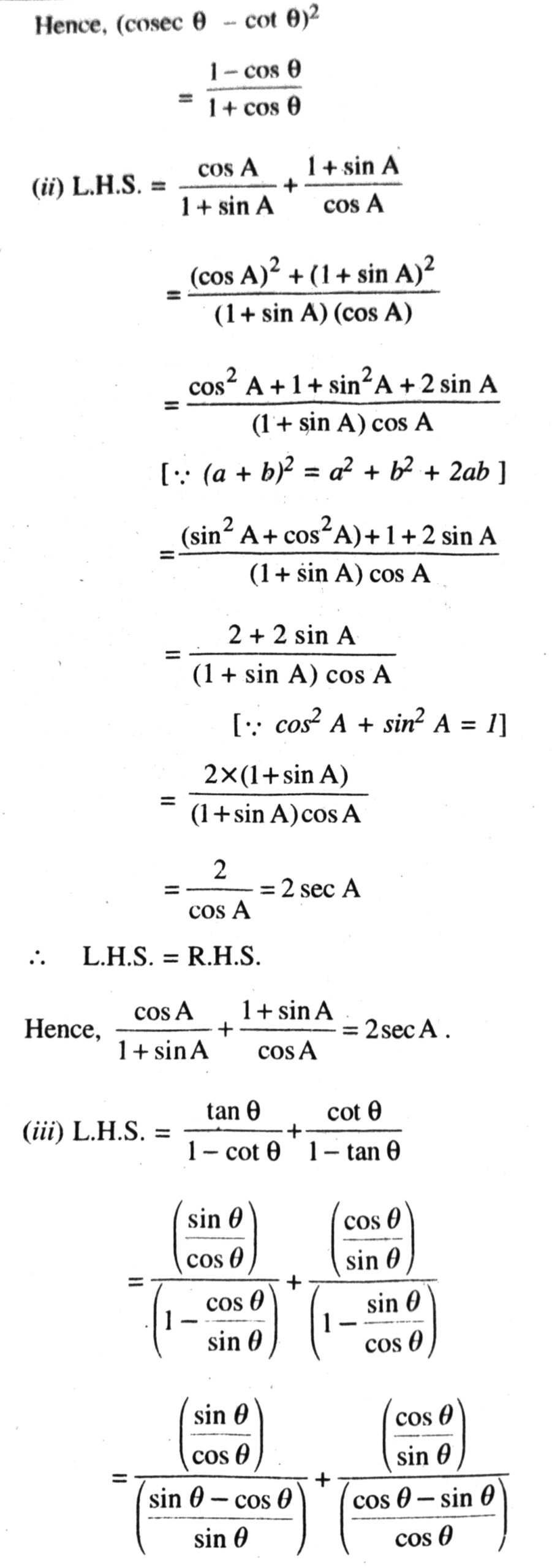
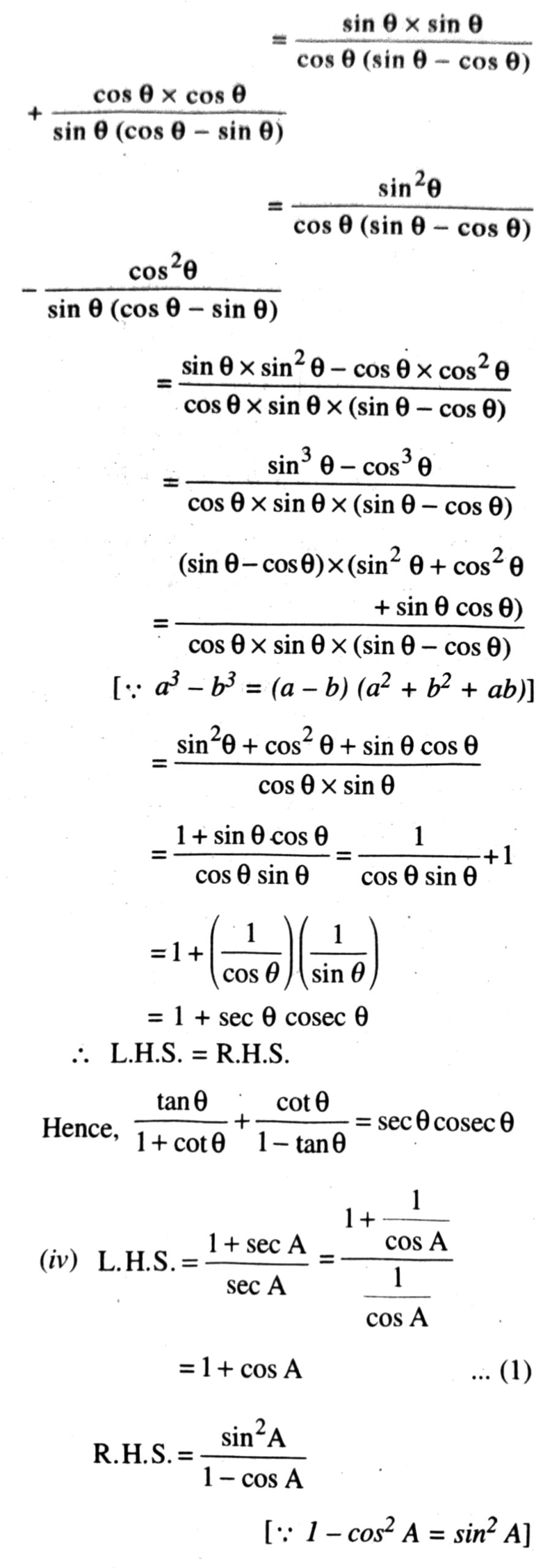

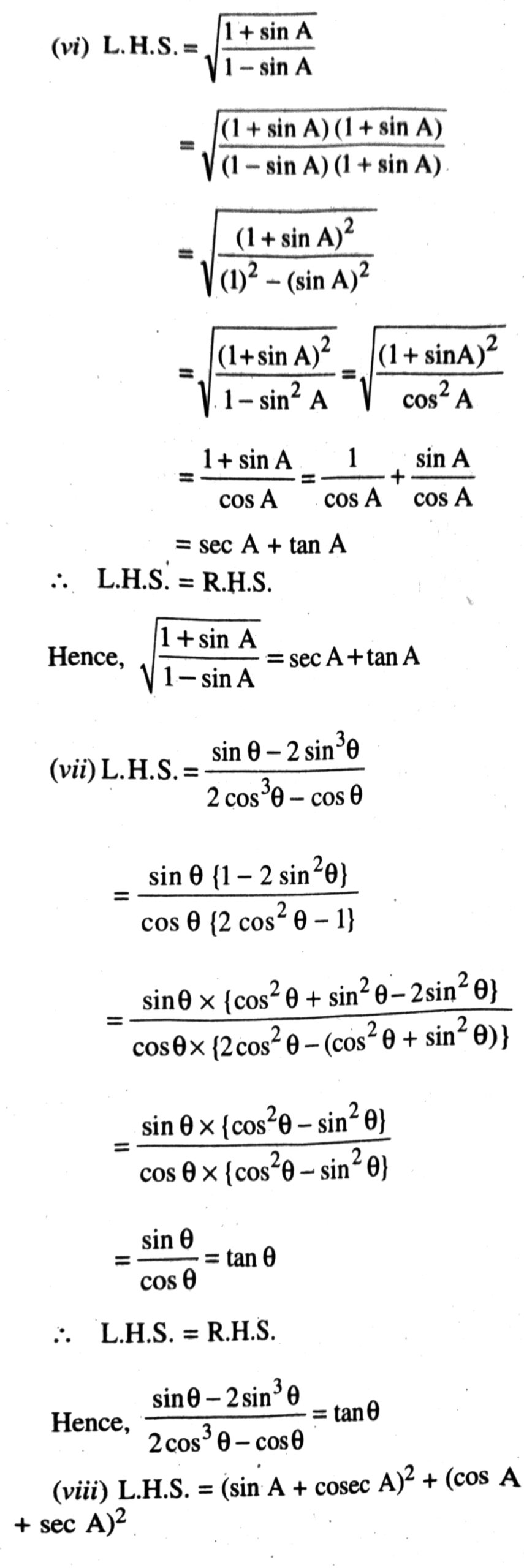
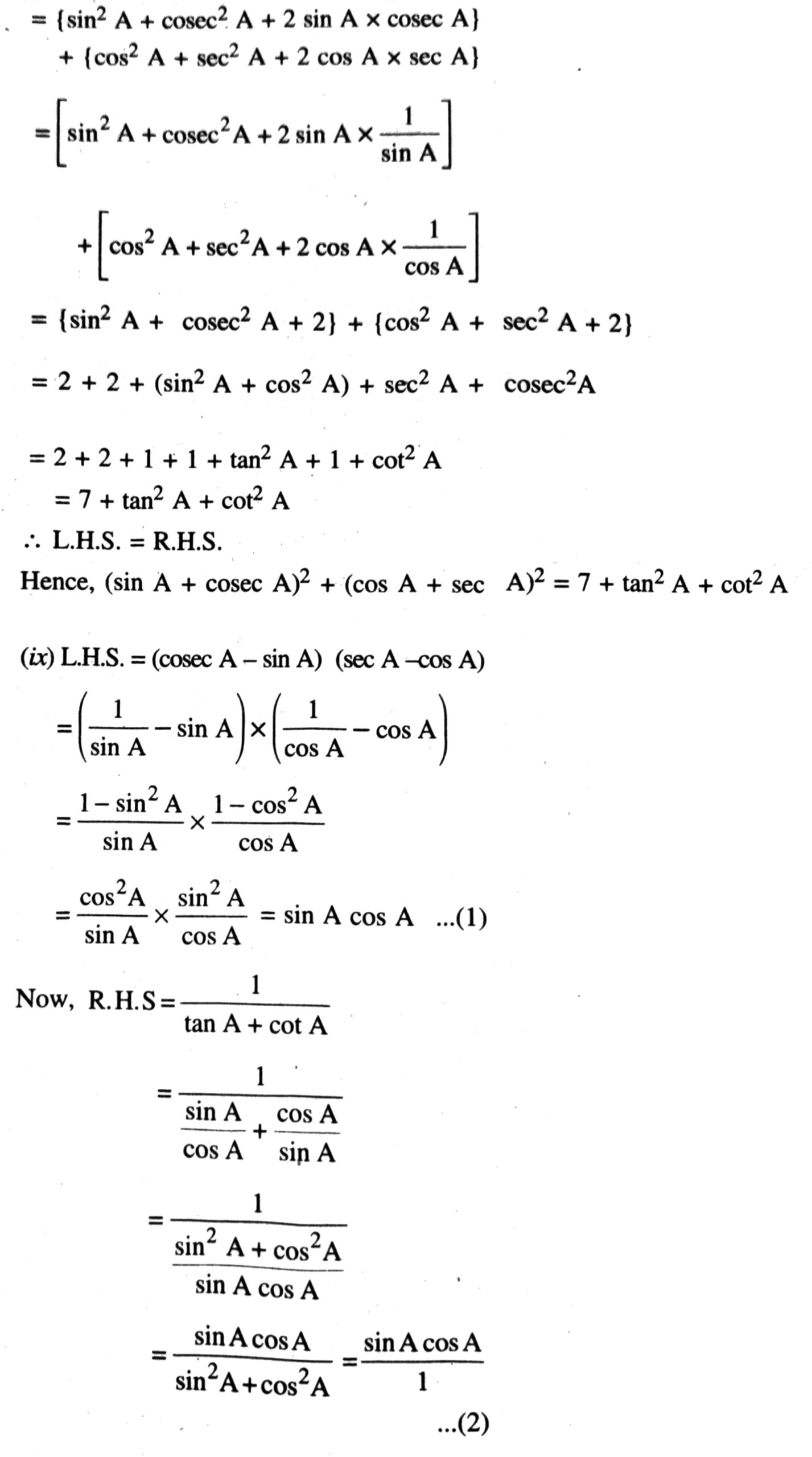
From (1) and (2), it is clear that
L.H.S. = R.H.S.
Hence, (cosec A – sin A) (sec A – cos A)
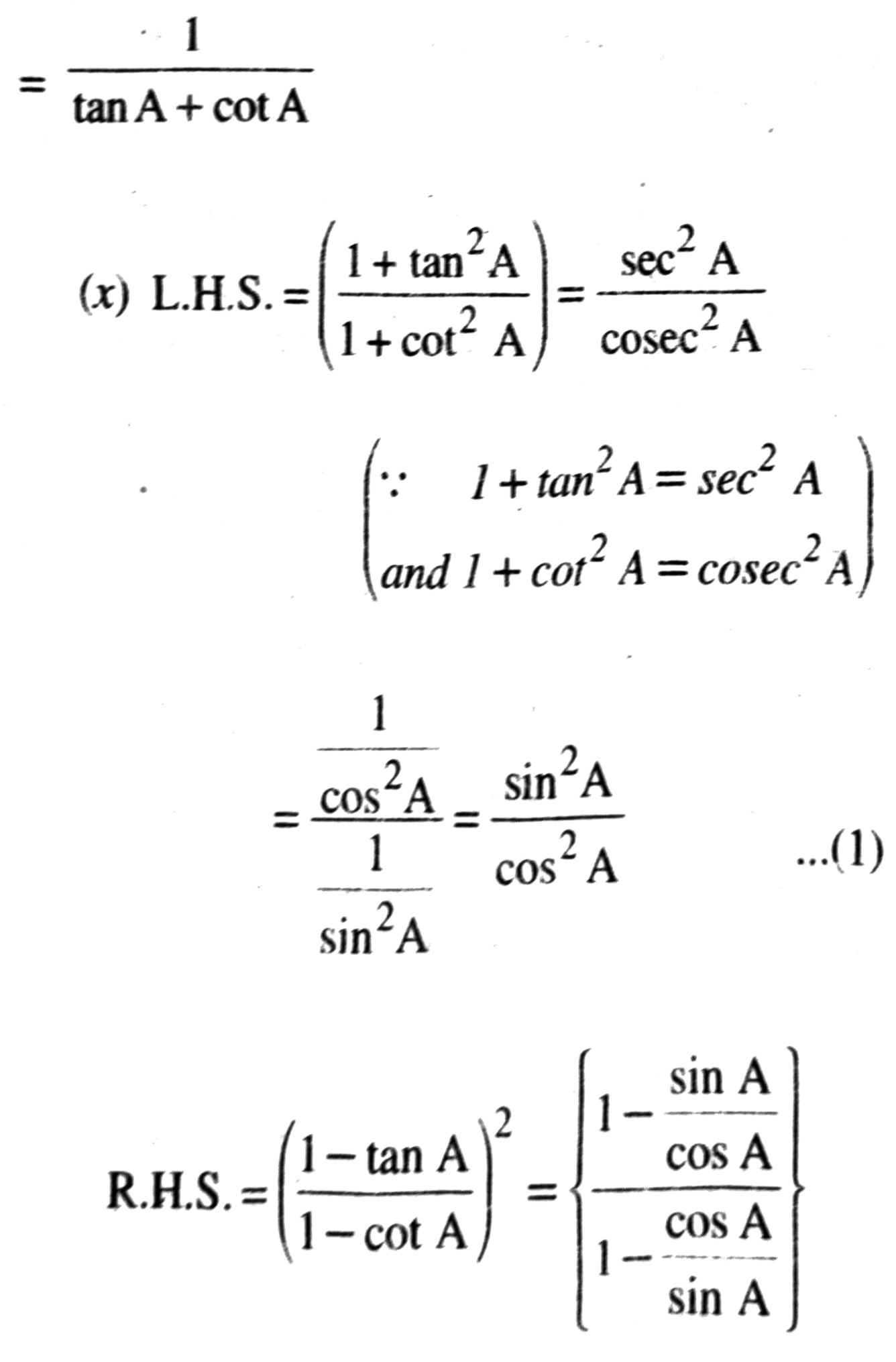
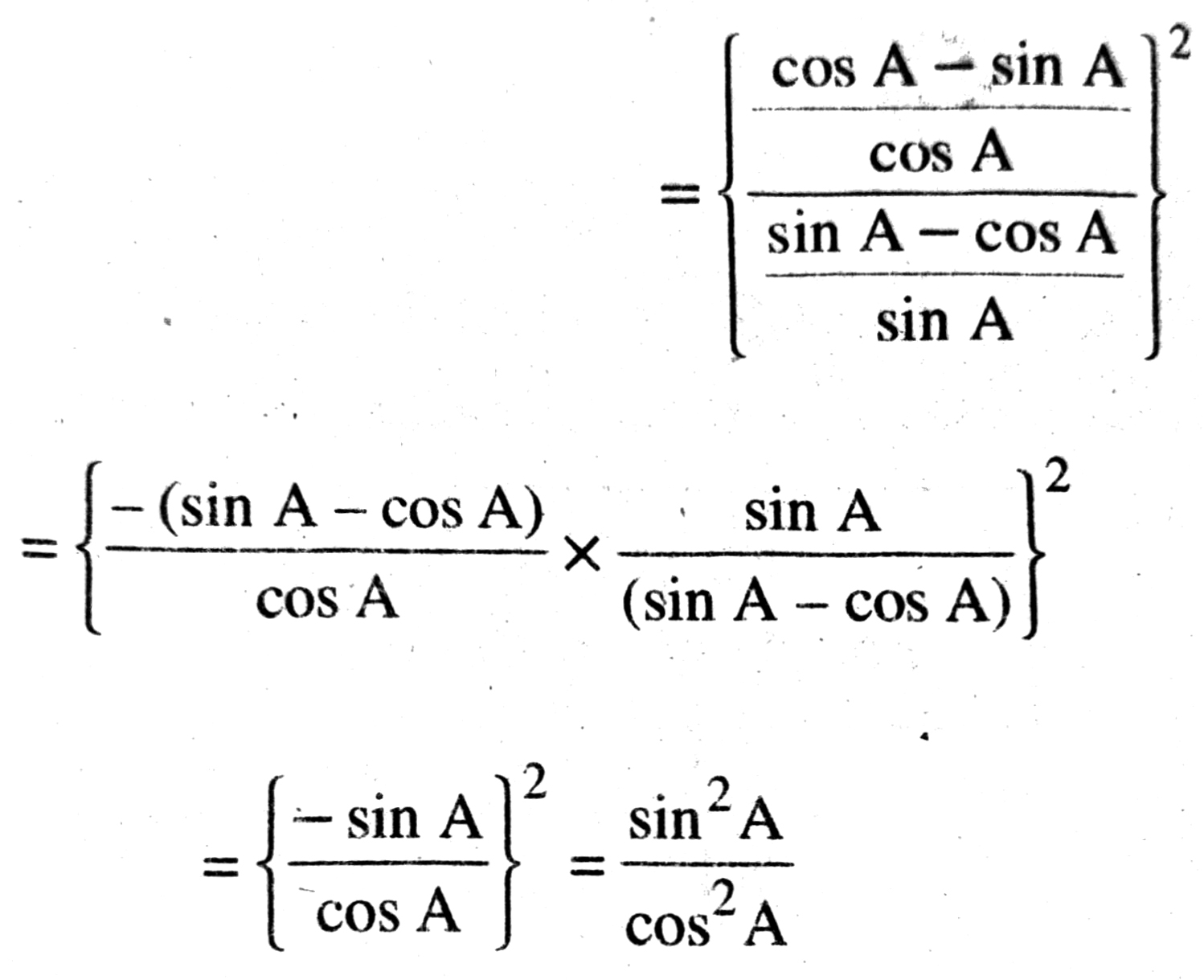
From (1) and (2), it is clear that
L.H.S. = R.H.S.
Hence,
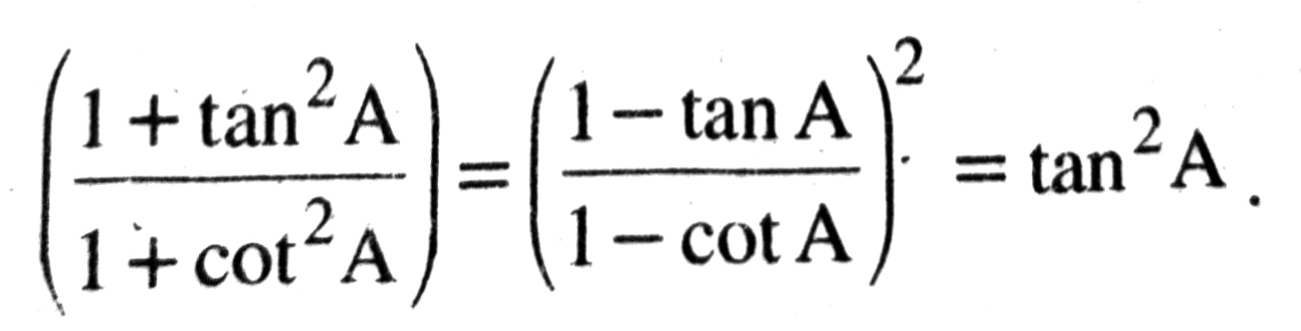
Follow on Facebook page – Click Here
Google News join in – Click Here
Read More Asia News – Click Here
Read More Sports News – Click Here
Read More Crypto News – Click Here